Аналитическое решение задачи потребительского выбора

В силу выявленных свойств, которыми должно обладать решение задачи потребительского выбора, переформулируем задачу следующим образом:

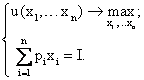
В новой формулировке задача потребительского выбора представляет собой задачу нелинейного программирования.

Для решения данной задачи составим функцию Лагранжа:

и найдем ее точки максимума. Точки, в которых функция Лагранжа достигает своего максимума, находятся среди стационарных точек, удовлетворяющих условиям:

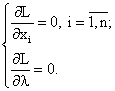
Эластичность функции

В ходе анализа различных экономических процессов очень часто используется понятие эластичности функции, которое тесно связано с понятием дифференцирования функции.

Эластичностью функции по аргументуназывают предел отношения приращения функции к приращению аргумента, в случае, когда приращение аргумента стремится к нулю:

где - предельное значение функции в данной точке,- среднее значение функции в данной точке.

Эластичность позволяет нам оценить на сколько процентов изменит свое значение функция при изменении значения аргумента на один процент.

. Используя понятие эластичности, выясним: как реагирует спрос на тот или иной товар в ответ на изменение цены того или иного товара и дохода потребителя:

если , то говорят о том, что спрос на данный товар не эластичен по отношению к цене данного товара (однопроцентное увеличение цены изменяет спрос на товар меньше чем на один процент).

если , то говорят о спросе с единичной эластичностью по отношению к цене данного товара (однопроцентное увеличение цены изменяет спрос на товар на один процент).

если , то говорят о эластичном спросе по отношению к цене данного товара (однопроцентное увеличение цены изменяет спрос на товар больше на один процент).

если , то говорят о совершенно эластичном спросе по отношению к цене данного товара.

если , то говорят о спросе с нулевой эластичностью по отношению к цене данного товара (изменение цены никак не влияет на изменение спроса на данный товар).

Модель Леонтьева многоотраслевой экономики (балансовый анализ)

Цель балансового анализа - ответить на вопрос, возникающий в макроэкономике и связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объем производства каждой из n отраслей, чтобы удовлетворить все потребности в продукции этой отрасли? При этом каждая отрасль выступает, с одной стороны, как производитель некоторой продукции, а с другой - как потребитель продукции и своей, и произведенной другими отраслями.

Связь между отраслями, как правило, отображается в таблицах межотраслевого баланса. Математическая модель, позволяющая их анализировать, разработана в 1936 г. американским экономистом В. Леонтьевым.

Предположим, что рассматривается n отраслей промышленности, каждая из которых производит свою продукцию. Часть продукции идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другая часть предназначена для конечного (вне сферы материального производства) личного и общественного потребления.

Рассмотрим процесс производства за некоторый период времени (например, год).

Введем следующие обозначения:

Х_i - общий (валовой) объем продукции i-й отрасли (i = 1,2,...,n);

x_ij - объем продукции i-й отрасли, потребляемой j-й отраслью в процессе производства (i,j = 1,2,...,n);

Y_i - объем конечного продукта i-й отрасли для непроизводственного потребления.

- условно-чистая продукция j-ой отрасли, включающая оплату труда, чистый доход и амортизацию.

Чистая продукция отрасли – разность между валовой продукцией отрасли и продукцией всех отраслей на производство этой отрасли.

Так как валовой объем продукции любой i-й отрасли равен суммарному объему продукции, потребляемой n отраслями, и конечного продукта, то

, (i = 1,2,...,n). (1)

Эти уравнения (их n штук) называются соотношениями баланса (по строкам таблицы)

Будем рассматривать стоимостный межотраслевой баланс, когда все величины, входящие в уравнения (1), имеют стоимостное выражение.

Итог материальных затрат любой отрасли и ее условно чистой продукции равен валовой продукции этой отрасли, поэтому

, (j = 1,2,...,n). (2)

Эти уравнения (их n штук) называются соотношениями баланса (по столбцам таблицы)

Производящие отрасли	Потребляющие отрасли				Конечный продукт	Валовой выпуск
	1	2	…	n
1 2 … n	…	…	… … …	…		…
Условно чистая продукция			…
Валовой продукт			…

Балансовый характер таблицы выражается в том, что

Введем коэффициенты прямых затрат: , (i,j = 1,2,...,n), (3),

показывающие затраты продукции i-й отрасли на производство единицы продукции j-й отрасли.

Можно полагать, что в некотором промежутке времени коэффициенты будут постоянными и зависящими от сложившейся технологии производства. Это означаетлинейную зависимость материальных затрат от валового выпуска, т.е.

, (i,j = 1,2,...,n), (3)

вследствие чего построенная на этом основании модель межотраслевого баланса получила название линейной.

Теперь соотношения баланса (1) примут вид:

, (i = 1,2,...,n). (4)

Обозначим ;;,

Где X - вектор валового выпуска; A - матрица прямых затрат (технологическая или структурная матрица); Y - вектор конечного продукта.

Тогда соотношения баланса (4) можно записать в матричном виде:

X = AX + Y. (5)

С помощью этой модели можно выполнять три вида плановых расчетов:

1. Задав в модели величины валовой продукции каждой отрасли Х_i можно определить объемы конечной продукции каждой отрасли Y_i

.

Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска X, который при известной матрице прямых затрат A обеспечивает заданный вектор конечного продукта Y.

Перепишем уравнение (5) в виде:

. (6)

Если матрица невырожденная, т.е. ее определитель не равен нулю, то

(7).

Матрица называетсяматрицей полных затрат.

Каждый элемент s_ij матрицы S есть величина валового выпуска продукции i-й отрасли, необходимого для обеспечения выпуска единицы конечного продукта j-й отрасли.

В соответствии с экономическим смыслом задачи значения x_i должны быть неотрицательны при неотрицательных значениях y_i и a_ij.

Матрица называетсяпродуктивной, если для любого вектора существует решениеуравнения (6). В этом случае и модель Леонтьева называетсяпродуктивной.

Существует несколько критериев продуктивности матрицы А. Согласно одному из них, матрица А продуктивна, если максимум сумм элементов ее столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы.

Практические и семинарские занятия – 10 часов.

Занятие 30. Решение задач линейного программирования графическим методом

Форма проведения занятия – краткое обсуждение теоретического материала, решение задач.

Отрабатываемые вопросы:

1. Составление математических моделей практических ситуаций.

2. Решение задач линейного программирования с двумя переменными графическим методом.

Занятие 31. Транспортная задача линейного программирования

Форма проведения занятия – проверка домашнего задания, обсуждение нового теоретического материала, решение задач.

Отрабатываемые вопросы.

1. Составление математической модели транспортной задачи;

2. Нахождение опорного решения (метод вычеркивания, метод северо-западного угла, метод минимальной стоимости);

3. Решение транспортной задачи линейного программирования методом потенциалов.

Занятие 32. Задача сетевого планирования и управления.

Форма проведения занятия – проверка домашнего задания, проведение самостоятельной работы по теме «Задачи линейного программирования», обсуждение нового теоретического материала, решение задач.

Отрабатываемые вопросы.

1. Плоские графы, эйлеровы графы, гамильтоновы графы, орграфы.

2. Построение сетевого графика и распределение ресурсов.

3. Расчет временных параметров сетевого графика.

4. Нахождение кратчайшего пути.

Занятие 33. Экономико-математические модели.

Форма проведения занятия – проверка домашнего задания, обсуждение результатов самостоятельной работы, обсуждение нового теоретического материала, решение задач.

Отрабатываемые вопросы.

1. Функции полезности.

2. Кривые безразличия.

3. Модели поведения фирмы в условиях совершенной и несовершенной конкуренции.

4. Экономическое равновесие.

Занятие 34. Контрольная работа № 6 по теме «Экономико-математические методы и модели».

Форма проведения занятия – проверка домашнего задания, проведение контрольной работы № 6 по теме «Экономико-математические методы и модели».

Управление самостоятельной работой студента.

Консультации, опрос по теоретическому материалу, проверка и разбор домашней работы, а также результатов самостоятельной и контрольной работы (см. подробнее в Приложении 3).

Приложение 3 к рабочей программе дисциплины «Математика»