Экстремумы функций двух переменных

Точка называется точкой локального максимума функции , если для всех точек , принадлежащих достаточно малой окрестности точки , выполняется неравенство . Значение функции в точке максимума называется локальным максимумом функции.

Точка называется точкой локального минимума функции , если для всех точек , принадлежащих достаточно малой окрестности точки , выполняется неравенство . Значение функции в точке минимума называется локальным минимумом функции.

Точки максимума и минимума функции называются точками экстремума функции, а значения функции в этих точках называются экстремумами функции.

Необходимое условие существования экстремума функции двух переменных: если функция достигает экстремума в точке , то ее частные производные первого порядка в этой точке равны нулю, т. е.

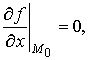
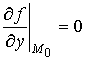
Точки, в которых частные производные равны нулю, называются стационарными точками. Не всякая стационарная точка является точкой экстремума.

Достаточное условие существования экстремума функции двух переменных: пусть - стационарная точка функции .

Обозначим:

;  ;

и составим соотношение

Тогда:

1) если , то значение функции - есть экстремум, причем это максимум, если и минимум, если ;

2) если , то значение функции экстремумом не является;

3) если , то требуется дальнейшее исследование.

Определение неопределенного интеграла

Функция F(x) называется первообразной от функции f(x) на отрезке [a;b], если во всех точках этого отрезка выполняется равенство F'(x)=f(x).

Если F(x) - первообразная функции f(x) , то F(x) + С тоже первообразная данной функции. Множество всех первообразных F(x)+C функции f(x) называется неопределенным интегралом функции f(x) и обозначается  . 

Символ    называется интегралом, f(x) называется подынтегральной функцией, f(x)dx называется подынтегральным выражением, x называется переменной интегрирования.

Свойства неопределенного интеграла

Неопределенный интеграл обладает следующими свойствами.

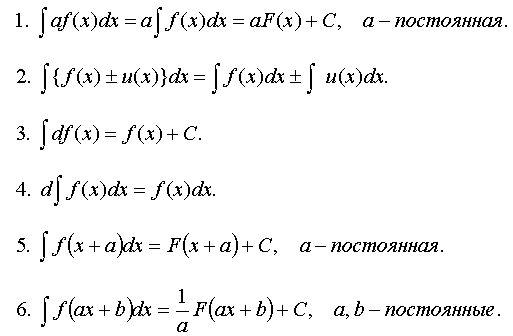
Таблица интегралов

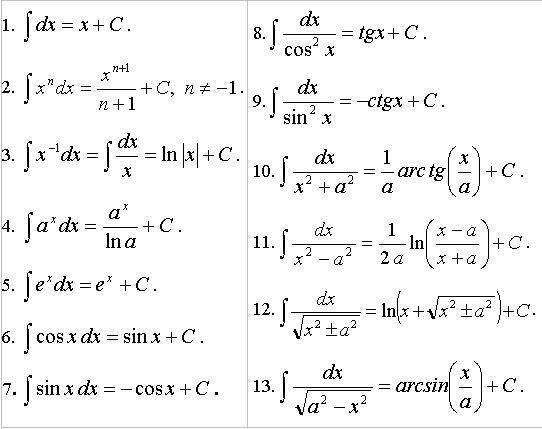
Задача интегрирования

Процесс интегрирования заключается в преобразовании подынтегрального выражения так, чтобы воспользоваться свойствами интеграла или методами интегрирования, преобразовать исходный интеграл в один или несколько табличных интегралов. В предыдущей лекции было установлено, что операция дифференцирования не выводит нас из класса элементарных функций. С операцией интегрирования дело обстоит иначе. Интегралы от некоторых элементарных функций не являются элементарными функциями. Например, интегралы    (интегральный синус, интегральный косинус, Интеграл Пуассона (интеграл ошибок)) не выражаются через элементарные функции (являются не берущимися).

Как правило, интегралы, с которыми приходится иметь дело в различных приложениях, являются «не берущимися», но существуют методы приближенных расчетов, позволяющие с достаточной точностью оценивать и вычислять такие интегралы.

Основные методы интегрирования

Вычисление интегралов с использованием основных свойств и таблицы простейших интегралов называется непосредственным интегрированием.

Метод замены переменной интегрирования (метод подстановки) является одним из самых эффективных приемов интегрирования. Он основан на следующей теореме:

Теорема. Пусть функция определена и дифференцируема на некотором промежуткеT, а X – множество значений этой функции, на котором определена функция . Тогда, если функцияимеет первообразную на множествеX, то на множестве Т справедлива формула:

Формула интегрирования по частям имеет вид:   .

При помощи интегрирования по частям исходный интеграл    сводят к более простому интегралу   

Лекция 10. (Информационная лекция с использованием средств мультимедиа).

Определенный интеграл. Геометрические приложения определенного интеграла.

Определенный интеграл как предел интегральной суммы, его основные свойства. Формула Ньютона-Лейбница для вычисления определенного интеграла. Методы интегрирования заменой переменной и по частям в определенном интеграле. Приложения интеграла к вычислению площадей плоских фигур, объема тела вращения. Использование определенного интеграла в экономике (дневная выработка, выпуск оборудования при постоянном темпе роста).

Геометрические приложения определенного интеграла.

Понятие определенного интеграла

Пусть функция f(x) определена на отрезке [a;b] . Внутри отрезка возьмем n последовательных точек x₁, x₂, . . . x_n (рис. 1).

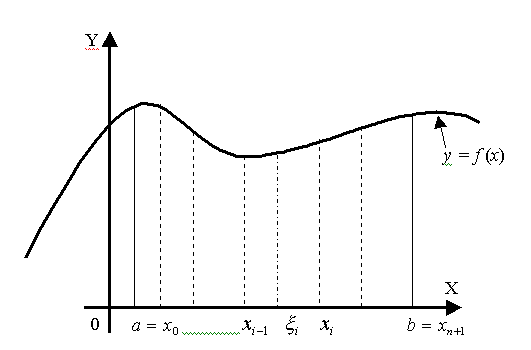
Рис. 1. Криволинейная трапеция

Обозначим a = x_o, b = x_n+1 . Весь отрезок разобьется на (n + 1) частичных промежутков. В каждом промежутке возьмем по точке   

Найдем значения функции    и длины промежутков h₁ = x₁ - x_o, ..., h_n+1 = x_n+1 - x_n.

Составим сумму    которая называется интегральной суммой. Обозначим через h длину наибольшего промежутка, т.е. h = maxh_i . Устремим n к бесконечности так, чтобы h стремилось к нулю.

Конечный предел последовательности S_n (если он существует) при h → 0 , который не зависит ни от способа разбиения отрезка [a,b] на n + 1 промежутков, ни от выбора точек ξ₁, ..., ξ_n+1 , называется определенным интегралом функции f(x) на отрезке [a,b] и обозначается 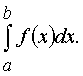   Функция f(x) называется интегрируемой функцией, число a называется нижним пределом интегрирования, число b называется верхним пределом интегрирования, отрезок [a,b] - отрезком интегрирования.

Непрерывная на отрезке [a,b] функция является интегрируемой на [a,b] .

2. Геометрический смысл определенного интеграла

Пусть функция y = f(x) ≥ 0 непрерывна (и значит, интегрируема) на отрезке [a,b] (рис. 2). Интегральная сумма S_n при f(x) ≥ 0 равна площади фигуры, составленной из прямоугольников со сторонами f(ξ_i) · h_i . Следовательно, предел последовательности S_n при h → 0 равен площади S криволинейной трапеции, т.е. фигуры, ограниченной линией y = f(x) , осью ОХ и прямыми x = a, x = b :   

Рис. 2

Свойства определенного интеграла

1. Постоянный множитель можно выносить за знак интеграла.

.

2. Интеграл от алгебраической суммы двух функций равен сумме интегралов от этих функций.

.

3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей.

.

4. Если на отрезке [a, b] , то и, т. е. обе части неравенства можно почленно интегрировать.

Следствие. Пусть на отрезке [a, b] , где m и M некоторые числа. Тогда.

5. Теорема о среднем. Если функция f(x) непрерывна на отрезке [a, b], то найдется такое значение , что.

Формула Ньютона-Лейбница

Если у функции y = f(x) первообразная F(x) является элементарной функцией, то для нахождения определенного интеграла используют формулу Ньютона-Лейбница:

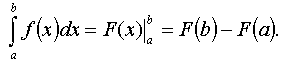
Замена переменной и интегрирование по частям в определенном интеграле

Теорема 1. Пусть функция имеет непрерывную производную на отрезке,и функция f(x) непрерывна в каждой точке x вида, где. Тогда, справедливо равенство

Теорема 2. Пусть функции иимеют непрерывные производные на отрезке. Тогда, справедливо равенство

Геометрические приложения определенного интеграла

Вычисление площадей в прямоугольных координатах

Пусть две функции y = f(x) и y = φ(x) непрерывны на отрезке [a,b] , причем f(x) ≥ φ(x) для всех    (рис. 3). Площадь S фигуры, ограниченной линиями y = f(x) , y = φ(x) и прямыми x = a, x = b , находится по формуле:  .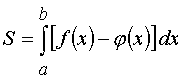

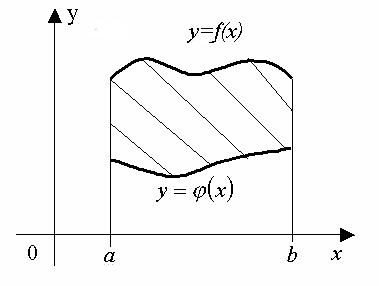
Рис. 3

Объем тела вращения

Объем V тела, полученного вращением криволинейной трапеции, ограниченной кривой y = f(x) (f(x) ≥ 0) , осью ОХ и прямыми x = a и x = b (a < b) вокруг оси Ox, находится по формуле:  .

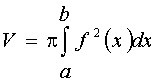Практические и семинарские занятия – 10 часов.

Занятие 18. Функции нескольких переменных: основные понятия. Частные производные первого порядка.

Форма проведения занятия – краткое обсуждение теоретического материала, решение задач.

Отрабатываемые вопросы:

1. Область определения и область значений.

2. Предел и непрерывность.

3. Частные производные первого порядка.

4. Градиент.

Занятие 19. Неопределенный интеграл: непосредственное интегрирование, метод подстановки, метод интегрирования по частям.

Форма проведения занятия – проверка домашнего задания, краткое обсуждение теоретического материала, решение задач.

Отрабатываемые вопросы:

1. Понятие неопределенного интеграла.

2. Таблица интегралов основных элементарных функций.

3. Непосредственное интегрирование.

4. Метод подстановки.

5. Интегрирование по частям.

Занятие 20. Интегрирование рациональных дробей, иррациональных и тригонометрических выражений.

Форма проведения занятия – проверка домашнего задания, проведение самостоятельной работы по теме «Неопределенный интеграл: простейшие методы вычисления», обсуждение нового теоретического материала, решение задач.

Отрабатываемые вопросы.

1. Понятие рациональной дроби.

2. Интегрирование рациональных дробей.

3. Интегрирование некоторых иррациональных выражений.

4. Интегрирование тригонометрических выражений.

Занятие 21. Определенный интеграл. Геометрические приложения определенного интеграла.

Форма проведения занятий – проверка домашнего задания, обсуждение результатов самостоятельной работы, обсуждение теоретического материала по новой теме, разбор примеров решения задач, решение задач.

Отрабатываемые вопросы.

1. Понятие определенного интеграла.

2. Метод замены переменной в определенном интеграле.

3. Интегрирование по частям в определенном интеграле.

4. Вычисление площадей плоских фигур.

Занятие 22. Контрольная работа № 4 по теме «Основы интегрального исчисления».

Форма проведения занятия – проверка домашнего задания, проведение контрольной работы № 4 по теме «Основы интегрального исчисления».

Управление самостоятельной работой студента.

Консультации, опрос по теоретическому материалу, проверка и разбор домашней работы, а также результатов самостоятельной и контрольной работы (см. подробнее в Приложении 3).
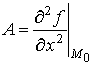