Контрольные задания

Найти решение системы линейных алгебраических уравнений . Для этого составить программу, реализующую один из описанных в этом разделе методов. Выбор итерационных методов решения систем должен быть обоснован предварительной проверкой матрицы системы на условие сходимости выбираемого метода. В случае применения итерационных методов принять относительную разницу между соседними приближениями вектора решения не более чем 0.000001. Оценить относительную погрешность полученного решения. Матрицу А и вектор b взять по номеру своего варианта, заменяя величину n номером своего варианта.

1–5.
6–10.
11–15.

16–20.
21–25.
26–30.

4. Интерполяция таблично заданных функций Справочная информация

Интерполяцией называется представление функции, значения которой заданы в виде таблицы, некоторой другой функцией, имеющей аналитическое описание и совпадающей с исходной при табличных значениях аргумента.

Простейшая задача, приводящая к интерполяции функций, заключается в следующем. В дискретные моменты времени x₁,x₂,...,x_nизмеряется значение некоторой физической величиныy, то есть наблюдается зависимость функцииyот аргументаx, и строится таблица

x	x1	x2	...	xn
y	y1	y2	...	yn

По этой таблице требуется восстановить значения функции при любых других значениях аргумента x из отрезка [x₁, x_n] или подобрать аналитическое выражение для приближающей функции y(x) достаточно простого вида, значения которой совпадали бы с заданными в таблице

.

Г

Рис.1.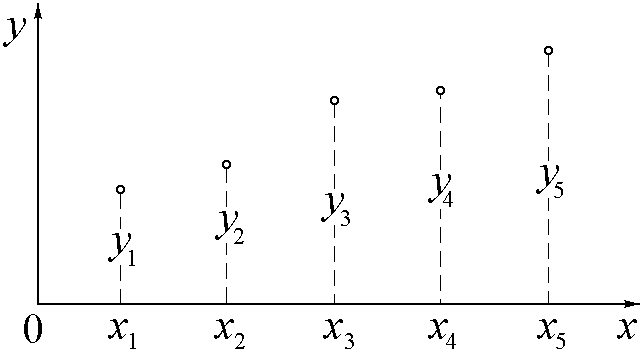

еометрический смысл задачи состоит в том, что через точки, которыми отображаются табличные значения аргумента и функции на поле декартовой системы координат x0y, как это показано на рис.1, и которые называются узловыми точками или узлами интерполяции, необходимо провести, по крайней мере, непрерывную линию, подобрав для неё аналитическое описание.

В зависимости от требований, которые накладываются на приближающую функцию, могут применяться различные формы её представления: линейная, квадратичная, кубическая или более высокого порядка. К простейшим из них относятся кусочно-линейная интерполяция, интерполяция кубическим сплайном и интерполяция многочленами, в частности, многочленом Лагранжа и другие.

Кусочно-линейная интерполяция

К

Рис.2.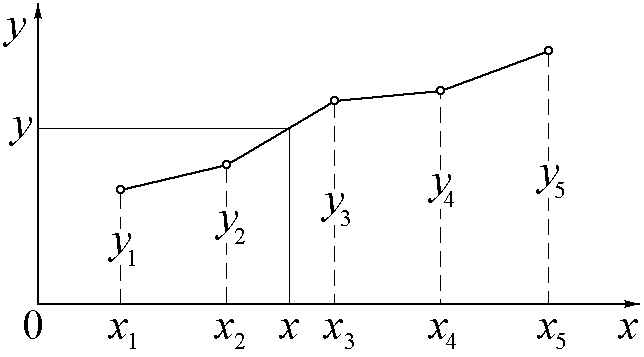

усочно-линейная интерполяция состоит в представлении таблично заданной функции на каждом отрезке между абсциссами узловых точек линейной зависимостьюy = a₁+ a₂x так, как это показано на рис.2. Коэффициенты a₁ и a₂ определяются для каждого отрезка [x_i–1, x_i] в отдельности из условий

.

В результате кусочно-линейная приближающая функция на отрезке [x_i–1,x_i] имеет вид

и является непрерывной, однако её первая производная оказывается уже кусочно-непрерывной функцией, которая в каждом узле интерполяции имеет точку разрыва первого рода. Это часто накладывает существенные ограничения на её дальнейшее использование.

x	0	1	2	3	4
y	2	0.5	1	4	4.5

Рассмотрим работу метода на примере кусочно-линейной интерполяции таблично заданной функции и поиска её значения при аргументе х = 1.5.

Для решения этой задачи строятся линейные функции для каждого отрезка между узловыми точками таблицы:

для отрезка [0, 1] между первой и второй точками

,

для отрезка [1, 2] между второй и третьей точками

,

для отрезка [2, 3] между третьей и четвёртой точками

,

для отрезка [3, 4] между четвёртой и пятой точками

.

Таким образом, табличная функция в случае кусочно-линейной интерполяции представляется в виде функции

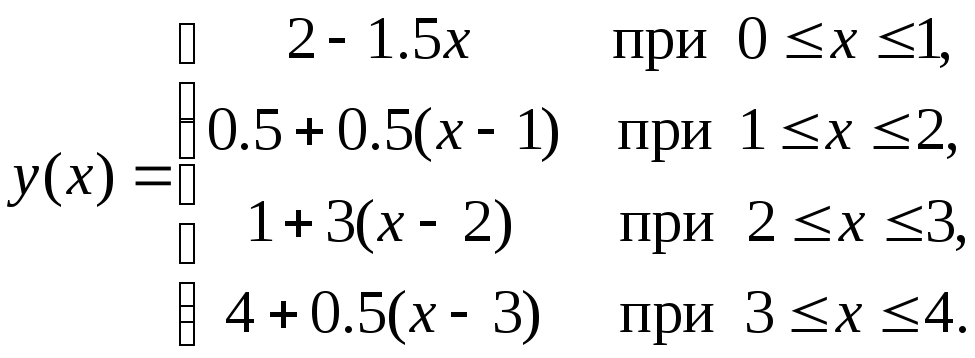
Значение интерполирующей функции в заданной точке x= 1.5, принадле­жа­щей отрезку [1, 2], будетy(1.5) = 0.5 + 0.5(1.5 – 1) = 0.75.

Многочлен Лагранжа (J.L.Lagrange, 1795)

Представляет собой случай полиномиального представления приближающей функции. Она ищется в виде линейной комбинации базисных функций _k(x), которые должны быть определены для всего отрезка интерполяции [x₁, x_n] и линейно независимы, а их количество должно быть равно числу узлов таблично заданной функции

.

Коэффициенты a₁, a₂,..., a_n определяются исходя из условий равенства значений приближающей и исходной функций при табличных значениях аргумента, что сводит задачу к системе n линейных алгебраических уравнений относительно них, а в качестве функций _k(x) используются полиномы (n–1)-й степени

,

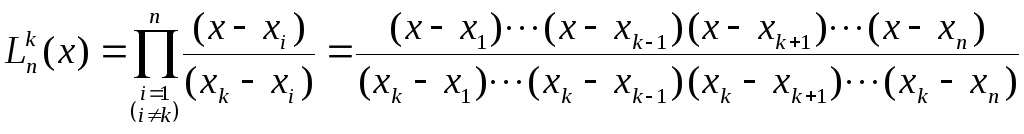которые для пяти узловых точек записываются в виде

,

…………………………………………

.

Г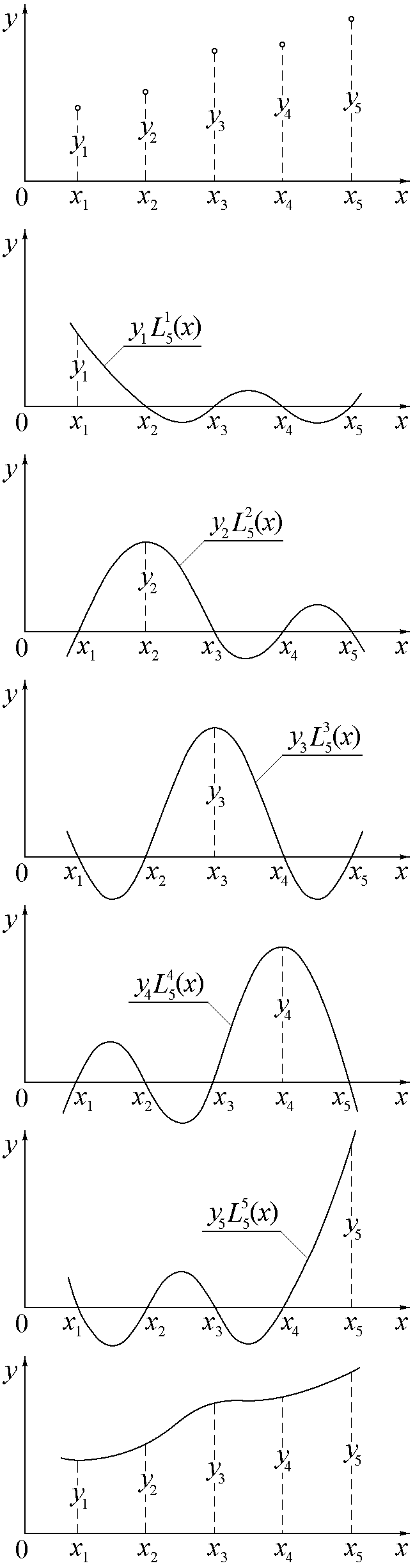рафики этих полиномов пред­ставлены на рис.3. Для каждого полинома характерно то, что для всех значенийx_i узловых точек он принимает нулевые значения, кроме k-ой, где его значение равно единице.

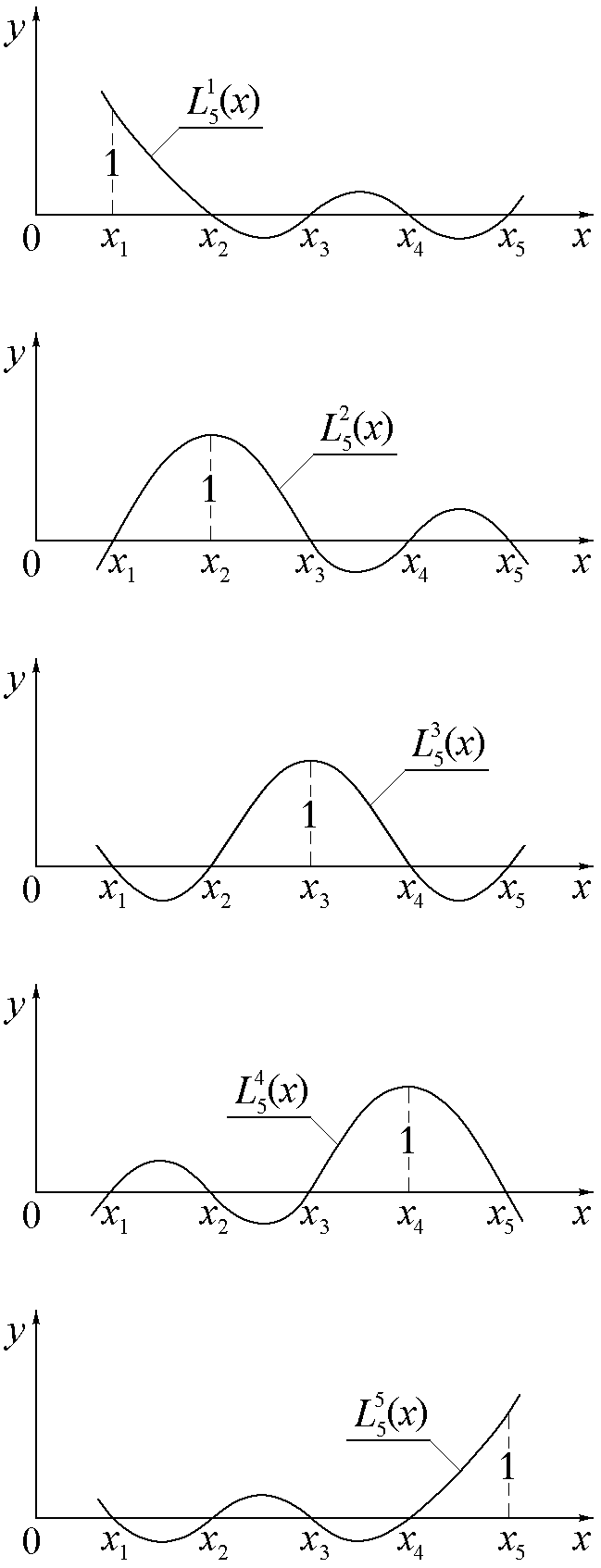
Рис.4.

Рис.3.

При таком выборе базисных функций коэффициенты приближающей функции оказываются ординатами таблично заданной функции, а сама она приобретает характерный для многочлена Лагранжа вид

.

Процесс построения интерполирующего многочлена Лагранжа для пяти узловых точек показан на рис.4.

x	0	1	2	3
y	2	0.5	1	4

Рассмотрим работу метода на примере интерполяции по Лагранжу таблично заданной функции и поиска её значения при х = 1.5.

Сначала строятся четыре базовых полинома:

,

,

.

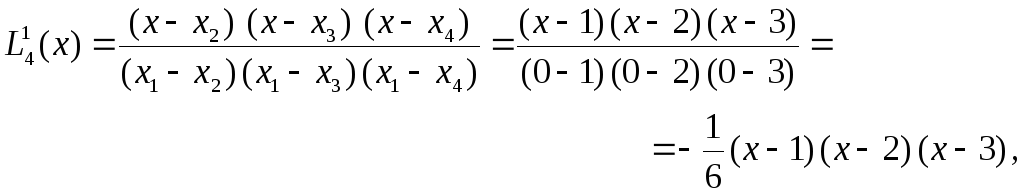
Они позволяют записать интерполирующий многочлен Лагранжа в виде

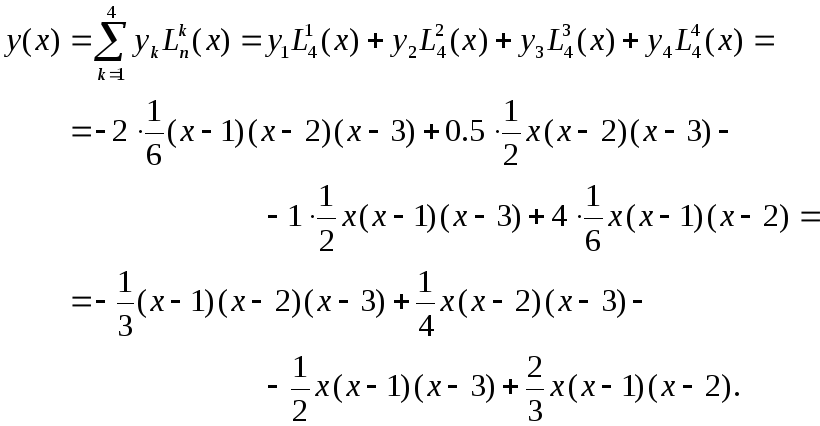
Для аргумента x= 1.5 многочлен Лагранжа даёт значение

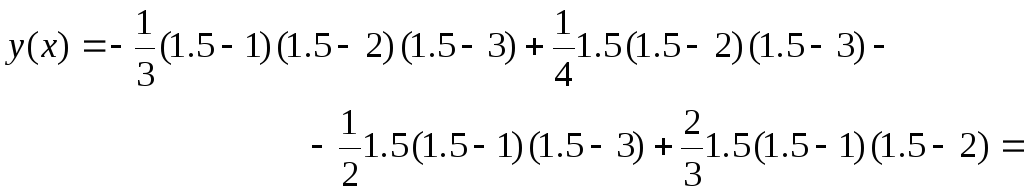
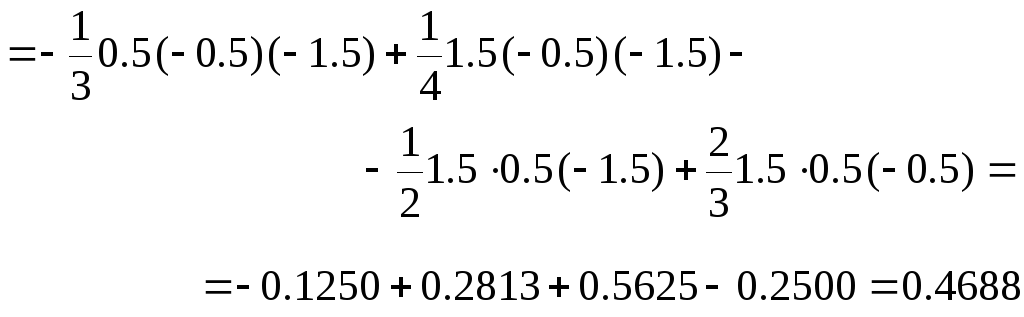
Интерполяция кубическим сплайном (I.J.Schoenberg, 1946)

Сплайнами называется широкий класс приближающих функций, используемых для кусочной интерполяции с использованием различных функций. В их число входят полиномы, в частности, кубический полином. При его использовании табличная функция внутри каждого отрезка [x₁, x₂], [x₂, x₃],…,[x_i, x_i+1],…,[x_n–1, x_n] представляется следующим образом

,

,

……………………………………………………………………

,

……………………………………………………………………………

г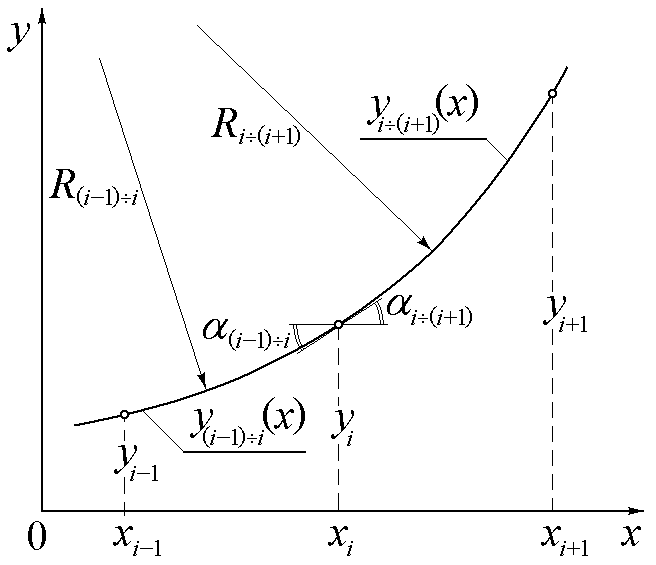де нижние индексы интерполирующих функций, записанные через тире, указывают на номера узлов, между которыми проведён сплайн (см. рис.5).

О

Рис.5.

трезки образуют область определения приближающей функции. Вычисление её коэффициентовa_i (i=1,2,3,…,4(n–1)) осу­­щест­вля­ет­ся исходя из следующих условий. По определению, значения сплайна в узловых точках должны совпадать с соответствующими значениями таблично заданной функции

, .

Эти условия дают 2(n – 1) уравнений для определения коэффициентов сплайна.

Кроме этого, требуется, чтобы полином данного отрезка сопрягался с полиномами соседних отрезков, как по углу наклона касательной в узловых точках, так и по радиусу кривизны. Сопряжение по углу наклона соответствует равенству значений первых производных соседних полиномов в каждой узловой точке, а по радиусу – вторых производных. Это даёт ещё по два условия для каждой внутренней узловой точки

,

т.е. получается ещё 2(n – 2) уравнений. Таким образом, приведённые выше соотношения дают (4n – 6) уравнений для определения коэффициентов a_i и для доопределения системы не хватает ещё двух уравнений. С целью построения недостающих уравнений можно задавать в граничных точках значения угла наклона касательной (исходя из физической сути задачи или с помощью интерполяции по 2÷4-м крайним точкам с последующим вычислением производной)

.

Возможны и иные способы задания граничных условий. Например, можно задавать граничные значения не первых, а вторых производных

.

Особый способ, называемый условием «нет узла» или «запрет стыка», состоит в приравнивании третьих производных полиномов на стыке двух крайних отрезков

.

Перечисленные условия дают систему из 4(n – 1) линейных алгебраических уравнений, позволяющую вычислить коэффициенты для каждого отрезка сплайна. Полученная интерполирующая функция будет непрерывной и гладкой вместе со своей первой производной, её вторая производная будет только непрерывной функцией, которая имеет точки излома в местах сопряжения сплайнов, т.е. в узловых точках.

Рассмотрим работу метода на примере таблично заданной функции (см. приведённую таблицу)

x	0	1	3
y	2	0.5	4

и поиска значения этой функции при х = 1.5.

Для решения задачи интерполяции заданной функции кубическими сплайнами требуется составить систему из 8-ми уравнений, позволяющую определить коэффициенты сплайнов для каждого из отрезков [0, 1] и [1, 3]

,

.

Их производные, необходимые для формирования системы, имеют вид

,

,

,

.

Тогда условия формирования сплайнов, записанные в последовательности узловых точек, будут выглядеть следующим образом

точка №1 (x = 0):

,

точка №2 (x = 1): ,

,

,

,

точка №3 (x = 3): ,

.

Н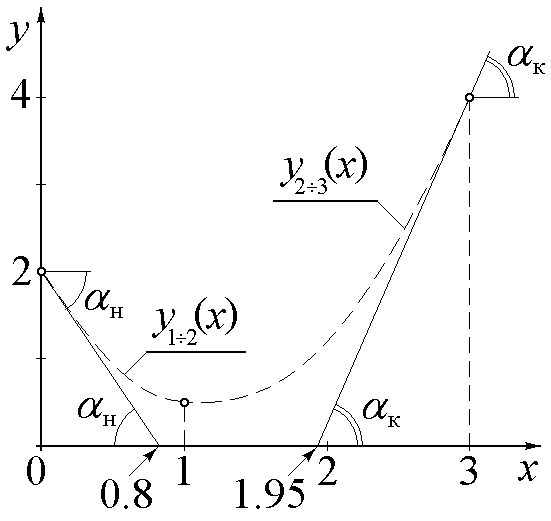едостающие значения тангенсов углов наклона касательных в крайних узловых точках могут быть вычислены из геометрических соображений, основанных на приближённом построении интерполирующей кривой (см. рис.6)

.

Т

Рис.6.

аким образом, система уравнений, определяющая коэффициенты кубических сплайнов, будет иметь вид

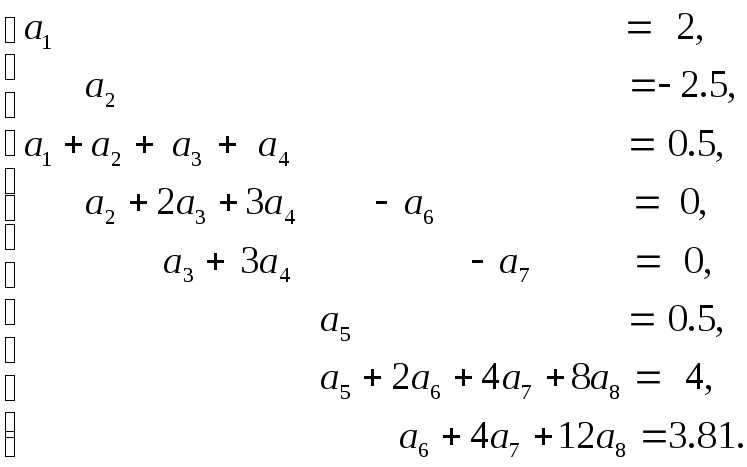
Её решение осуществляется каким-либо известным способом решения систем линейных алгебраических уравнений. В результате получается следующее её решение

a₁ = 2, a₂ = –2.5, a₃ = 0.9267, a₄ = 0.07333,

a₅ = 0.5, a₆ = –0.4267, a₇ = 1.147, a₈ = –0.02917.

При этом искомые сплайны будут иметь вид

,

,

а интерполирующая функция может быть записана как

Её значения при х = 1.5 будет

.

Приведённая выше схема сплайн-интерполяции достаточно трудоёмка. Поэтому в настоящее время используется её «экономичный» вариант, который основан на представлении сплайна в виде нескольких специально подобранных кубических полиномов

,

,

……………………………………………………………………………

,

где y_i – ординаты узловых точек, α_i – углы наклона графика сплайнов в узловых точках, h_i – расстояния между абсциссами i-й и (i+1)-й узловых точек, а полиномы имеют вид

, ,

, .

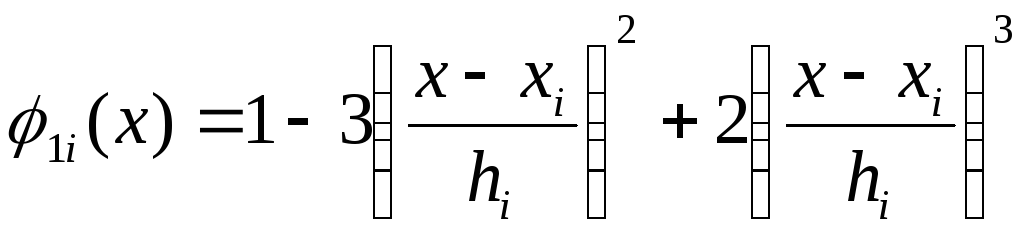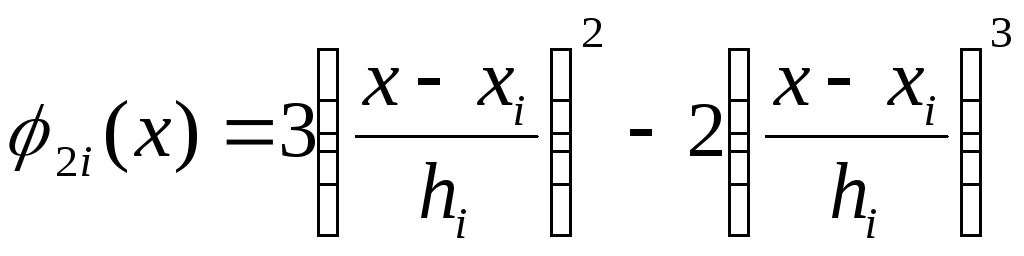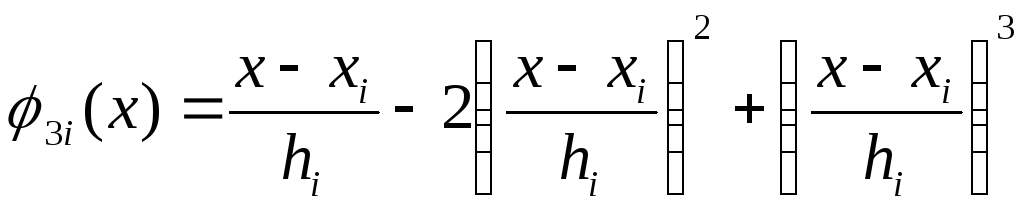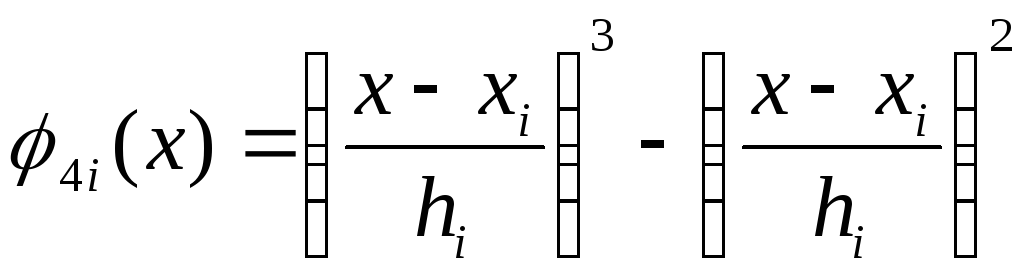Такой подход гарантированно сопрягает сплайны по местоположению узловых точек и по углу наклона касательных в них (равенство первых производных). Таким образом, задача сводится к необходимости сопряжения сплайнов в узловых точках только по радиусу кривизны (равенство вторых производных)

.

Эти (n – 2) уравнения служат для вычисления тангенсов углов наклона касательных в узловых точках. Недостающие два уравнения формируются по описанной выше схеме учёта граничных условий.

Для иллюстрации этого подхода рассмотрим решение предыдущей задачи.

Сплайны для каждого из отрезков [0, 1] и [1, 3] в соответствии с предлагаемым подходом имеют вид

,

.

Учитывая координаты узловых точек

x₁ = 0, x₂ = 1, x₃ = 3,

y₁ = 2, y₂ = 0.5, y₃ = 4,

можно вычислить расстояния между их абсциссами

h₁ = 1 и h₂ = 2

и переписать сплайны как

,

,

где

, ,

, ,

, ,

, .

Вторые производные сплайнов, необходимые для формирования системы уравнений, имеют вид

,

,

где

, ,

, ,

, ,

, .

Тогда условия формирования сплайнов, записанные в последовательности узловых точек, будут выглядеть следующим образом

точка №1 (x = 0): ,

точка №2 (x = 1): 



,

точка №3 (x = 3): .

Значения тангенсов углов наклона касательных в крайних узловых точках известны из предыдущего решения

.

В результате их подстановки в уравнение для 2-й точки получается одно уравнение для тангенса угла наклона касательных в этой точке

.

В итого получается следующее его значение

.

При этом искомые сплайны будут иметь вид

,

.

Тогда значение интерполирующей функции при х = 1.5 будет

.