30.Теор Руше.

Теор.1 Если две ф-ии , голоморфные внутри и на контуре Г, удовл. на Г услов-ям, то внутри Г ф-иииимеют одинаковое число нулей.

Док-во Поскольку , то, но, поэтому конец вектора, изображ., описывает замкнут кривую, целиком заключ. внутри круга с центром в т.1 и радиуса 1. Сл-но, соотв. вектор не делает ни одного оборота вокруг начала координат, и изменение аргументапри обходе т.z кривой Г равно 0. Измен-ие совпадает с изм-ем, откуда по принц. аргум-та вытек. рав-во нулей ф-ий

31.Принцип сохранения области

Теор.1 Мн-во D значений, принимаемых в нек-ой обл-ти G голоморфной ф-ией есть область. Иными словами, голоморфная ф-ия, не тождественная константе, всегда преобразует область в область. (Тут просто ультрамазафакерское доказательствово, так что не стал его включать)

Следствие(принцип максимума модуля): Ни в одной т.голом. ф.f(z) не может иметь максимума

32. Лемма об интегралах по дугам окружностей. Вычисление несобственных интегралов вида.

Для достаточно хорошего множества функций можно вычислить используя теорему о вычетах. Пусть.

Лемма: Пусть f-непрерывна на множестве , и пусть, тогда.

Теор: Пусть функция f-голоморфна в замыкании полуплоскости всюду кроме конкретного числа особых точек, лежащих в этой полуплоскости. Если, то

Сл: Пусть f-рациональная ф-я, знаменатель которой не имеет действительных нулей, а степень его не менее чем на 2 единицы больше чем степень числителя, то справедлива ф-я (1).

33. Лемма Жордана. Вычисление интегралов вида.

Лемма Жордана: Пусть f-непрерывная на множестве , для которогои пусть, тогда, если.

Теор: Пусть f-голоморфна в замыкании полуплоскости всюду кроме конечного числа особых точек, лежащих в этой полуплоскости. Если, то

Сл: Если ф-я f(z) при действительном z принимает действительные значения, то в условиях теоремы справедливы формулы:

Сл: Пусть f-рациональная ф-я, знаменатель которой не имеет действительных нулей, а степень его не менее чем на 2 единицы больше чем степень числителя. Тогда при справедливо. Если, кроме того,f(z) при действительном z действительные значения то справедливы формулы (1), (2).

34. Интегралы в смысле главного значения и их вычисление.

Распространение теоремы на тот случай когда f имеет конечное число особых точек .

Опр: Главные значения от интеграла f(x) на определены равенством:, где

Теор: Пусть f-голоморфна в замыкании полуплоскости всюду за исключением конечного числа особых точек, лежащих в этой полуплоскости, и конечного числа полюсовна действительной оси. Если, то

35. Целые и мероморные функции. Представление рациональной функции в виде суммы многочлена и простейших дробей.

Опр: Ф-я называется целой, если она голоморфна в . Среди элементарных ф-й целыми являются полиномы, показательные, тригонометрические и гиперболические.

Отличная от постоянной целая ф-я имеет наили полюс или существует особая точка.

Утв: Целая ф-я с полюсом является полиномом.

Действительно, если - полюс порядка, то вычитая главную часть ее ряда Лорана вполучим целую ф-юс устранимой особенностью на, следовательно ограниченную в. Согласно теореме Лиувилля

Итак 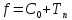- полином.

Опр: Целая ф-я с существованием особой точкой на называется целой трансцендентной ф-ей.

Утв: Целая трансцендентная ф-ия обозначается бесконечным степенным рядом

Более общим, чем класс целых, является класс мероморфных ф-ий.

Опр: Мероморфной называют ф-ию, голоморфную в Сz всюду за исключением точек, в которых f имеет полюсы.

К числу мероморфных относятся рациональные, частное от деления целой на целую.

Теор: f- мероморфная с конечным числом полюсов с является рациональной ф-ей.

Замеч: полученная ф-ла (1) дает представление рациональной ф-ии f в виде суммы (целой части) и простейших дробей.