6.Консервативность и порядок аппроксимации конечно-разностной схемы для линейного уравнения теплопроводности.

Консервативность.Свойство консервативности заключается в следующем:Если некоторое ДУ имеет дивергентный вид:(1)То проинтегрировав это уравнение по отрезку [a,b], мы получим(2) где что означает, что изменение некоторой величины М внутри отрезка [a,b] происходит благодаря разнице потоковFна границах отрезка.Аналогично определяется свойство консервативности (4) разностной схемы для конечно-разностного уравнения, где вместо интеграла подразумевается суммирование по всем ячейкам. Если потоки совпадаютF(b) =F(a), то очевидно.Произвольные схемы не обладают свойством консервативности. Это приводит к тому, что М изменяется во внутренних ячейках из-за рассогласования, не консервативности, или иначе, говорят, что во внутренних ячейках появляются фиктивные источники.Не трудно заметить, что схема (2) консервативна, просуммировав по всемj

получим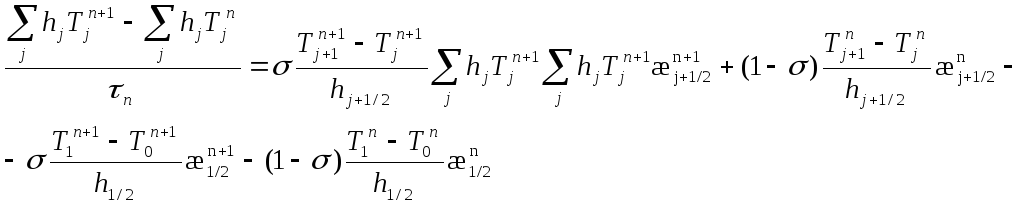

2.Порядок аппроксимации. Найдем, с какой точностью разностное уравнение (2) аппроксимирует (1). Для этого разложим переменную Т_jⁿ ( считая ее непрерывной Т_jⁿ=T(t,x) ) в ряд Тейлора в некоторой точке. Из симметрии схемы удобно выбрать точку (t_n+1/2,x_j) тогда:

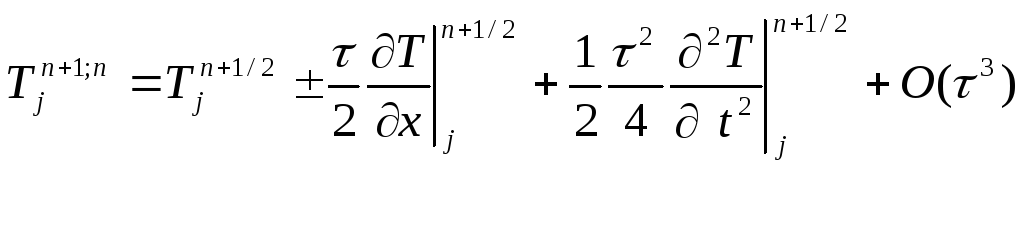
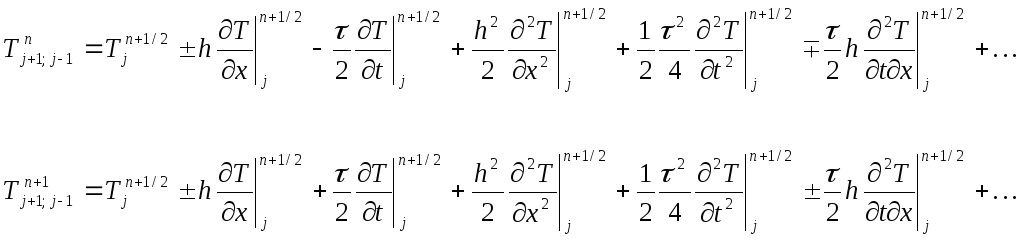
Подставим разложение в (2), предполагая для простоты выкладок æ, h=const,(3)

Отсюда следует, что при произвольном σ схема имеет первый порядок точности о(τ), а при σ = 1/2 – второй порядок о(τ²).

Центрированная схема с σ = ½, как наиболее точная , чаще применяется – называется схемой Кранка-Николсона.

7.Устойчивость и дисперсионные свойства конечно-разностной схемы для линейного уравнения теплопроводностиДискретизация дисперсионного уравнения изменяет его дисперсионные характеристики.Рассмотрим эти эффекты на примере линейного уравнения теплопроводности, т.к. дисперсионный аналог возможен только по отношению к линейным уравнениям.(1)Всякое решение исходного уравнения (1), в том случае когда=const, мот быть разложено в ряд (интеграл) по волнам.(2)Подставляем (2) в (1):(3)Разностное уравнение: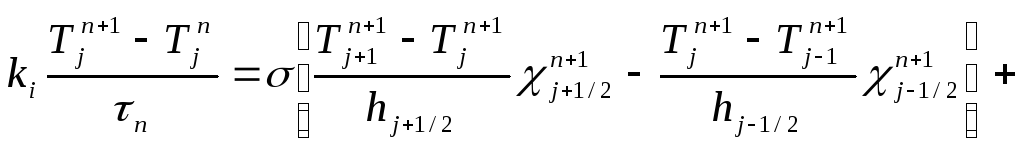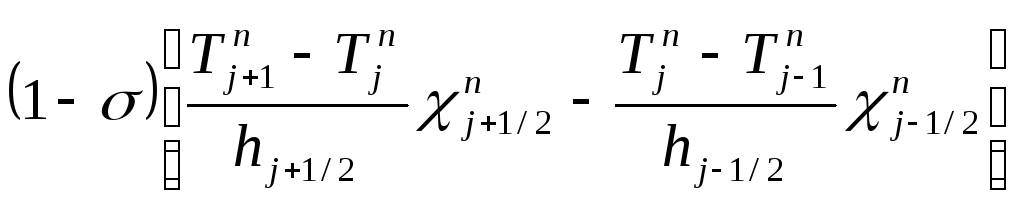(4)также линейно и, следовательно, имеет решение, которое может быть разложено в конечный ряд (сумму) по дискретным гармоникам. Подставляя (2) в (4) получим

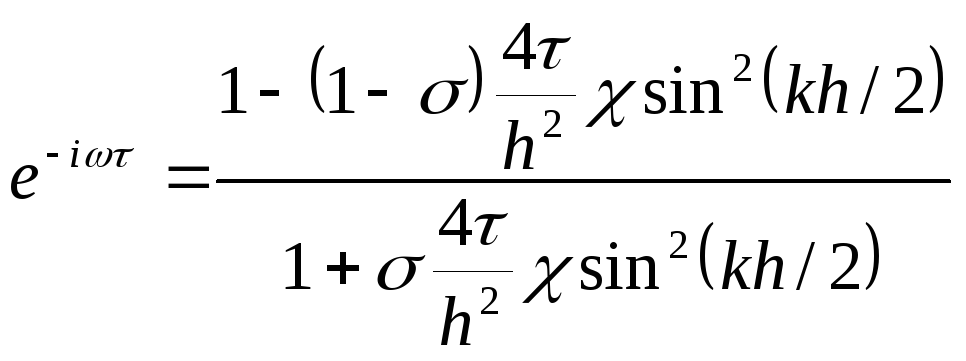,(5)В общем случае-комплексна:, где вещественная частьотвечает за дисперсию (волновые свойства, колебания), а инкрементза возбуждение или подавление гармоник (в случае затухания обычно говорят о декременте). Согласно (3), для любой простой волны с волновым числомk, при, т.е. инкремент отрицателен, гармоники затухают.Дисперсионное уравнение (5), соответствующее разностной схеме, отличается т точного дисперсионного уравнения (3), но в пределе малыхhи() переходит в (3). В зависимости от величинывозможны различные ситуации.I.1)-колебаний нет, «чистое» затухание. 2)-колебания с частотой(T=2) для волн си затухание.II. 3)-колебания с затуханием 4)-существует область, где

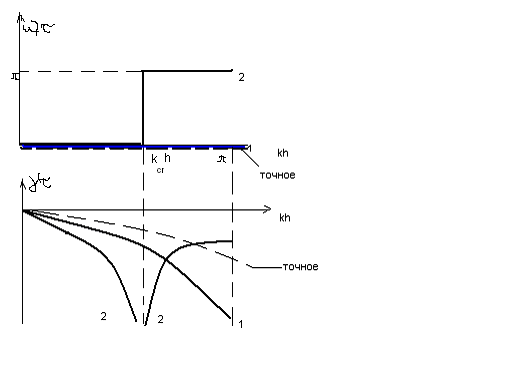
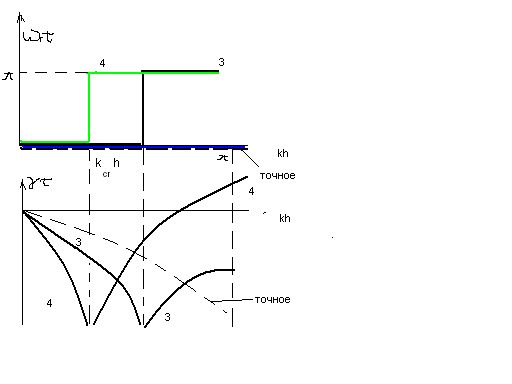
Изменение от 0 доприводит к появлению короткопериодических осцилляций в численном решении (им подвержены волны с большим, т.е. короткие волны). Длинные волны () имеют правильный закон дисперсии, в то время как короткие подвержены аномально большой диффузии. Для волн ссхема вообще не прозрачна. Наличие гармоник созначает возникновение неустойчивости, имеющей нефизическую численную природу. Чисто неявные схемы устойчивы при любом шаге интегрирования. Чисто явные ограничено устойчивы. Шагпри этом должен быть меньше времени распространения возмущения через одну произвольную ячейку. В конкретном случаехарактерного диффузионного времени.

8.Нелинейное уравнение теплопроводности, волновые решения, расчет движения тепловой волны.

Уравнение теплопроводности: (1)Нелинейная зависимость коэффициента теплопроводностиот Т приводит к появлению нового типа решений уравнения (1) в виде стационарных бегущих волн, сохраняющих свою форму. Существование данного феномена связано с балансом двух конкурирующих эффектов: нелинейности, которая «укручивает» фронт волны, и диффузии, которая фронт размывает.ПустьИщем решение (1) в виде бегущей волны:, гдеu=const –скорость волны.,,С учетом данных соотношений переписываем (1):(2)

П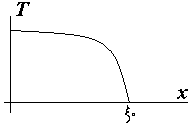роинтегрируем (2):(3)Выражение (3) легко интегрируется, частным решением является степеное:(4)Вблизиповедение Т () сильно нелинейно (см. рис). В этом случае линейный анализ устойчивости схемы «не срабатывает», т.к. устойчивость будет зависеть также от Т и ее градиентов. Особенность Т в точкекак правило, оказывается летальной для всех явных схем, в то время как неявные воспринимают ее безо всяких проблем.