Плоское движение. Определение ускорений точек

1. Аналитический способ,

Зная уравнения движения точки x_B = x_B(t); y_B = y_B(t), находим

; ; .

2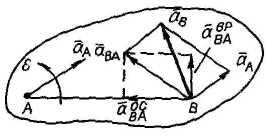.Теорема о распределении ускорений. Дифференцируя равенство, получим

- ускорение точки B при вращении фигуры вокруг полюса A

; модули ; ; .

Т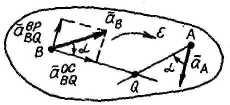аким образом, формула распределения ускорений точек плоской фигуры .

3. Мгновенный центр ускорений (МЦУ).

Ускорения точек при плоском движении можно опре­делять по формулам вращательного движения, исполь­зуя понятие МЦУ. МЦУ - точка, связанная с плос­кой фигурой, ускорение которой в данный момент времени равно ну­лю (a_Q = 0).

Положение МЦУ определяется формулами

; .

Принимая точку q за полюс, имеем для произвольной точки

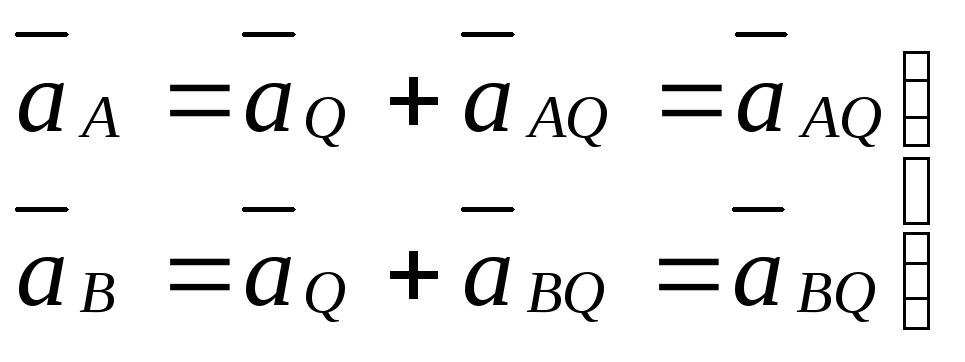, тогда

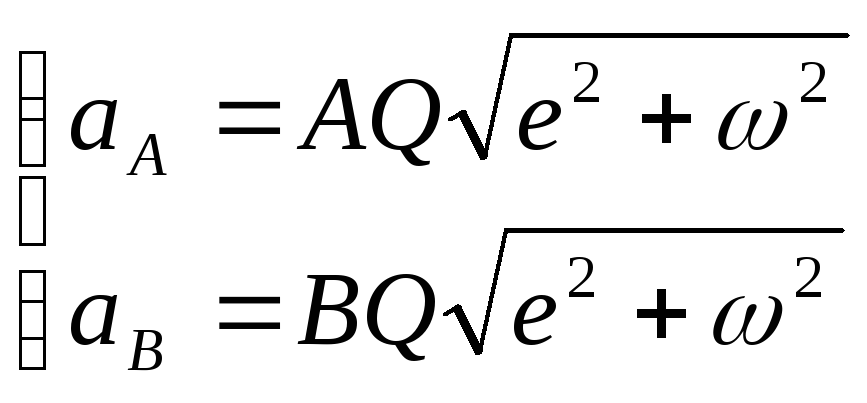
Отсюда , т.е. ускорения точек плоской фигуры пропорциональны их расстояниям до МЦУ.

П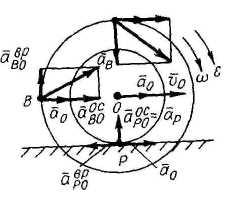римеры

1). Колесо вагона катится без скольжения по прямолинейному рельсу. Определить ускорения то­чек B и P, а также положение МЦУ, если v₀ = 50 см/с; а₀ = 29 см/с²; r = 50 см; R = 60 см.

Решение

1. Точка P - МЦС колеса, следовательно, угловая скорость с^-1

2. Угловое ускорение e получим, учитывая, что PO = г = const:

с^-2.

3. Ускорение точки B , где см/с²; см/с²; см/с².

4. Ускорение точки P (МЦС) ,где см/с²; см/c². Так как в данном случае , то ;см/с². Аналогичным образом определяются ускорения других точек.

5) зная а₀, w и e, находим поло­жение мгновенного центра ускорений колеса ;см.

Повернув вектор в направленииe на угол a и отложив отрезок OQ, получаем точку Q - МЦУ колеса.

Тогда

и т.д.

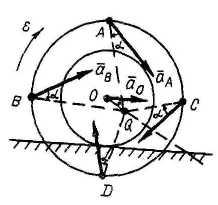
Примеры (продолжение)

2). В данный момент времени кри­вошип OA вращается с w_OA= 1c^-1, e_OA =4 с^-2. Каток катится без скольжения. OA=AB = 4R = 4 м. Определить v_A, v_B, w_AB, w_k, a_A, a_B, e_AB, e_k.

Решение

Определение скоростей: м/c; .

МЦС звена AB - точка P_AB. Поэтому угловая скорость с^-1;  м/с; угловая скорость с^-1.

О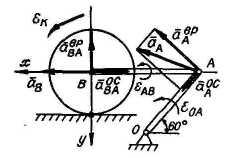пределение ускорений:

ускорение точки A , м/с²; м/с²; ;м/с².

Ускорение точки B , (1)

Где м/с², .

Предположив, что и . Направлены как на рисунке, проектируем (1) на оси х (||AB) и у (AB):

м/с²;

м/с².

Знак « - » означает, что действительное направление противоположно показанному на рисунке.

Так как , тос^-2.

Направление e_AB определяется направлением вектора относительно т. A. Поскольку bp_k= const, то с^-2.

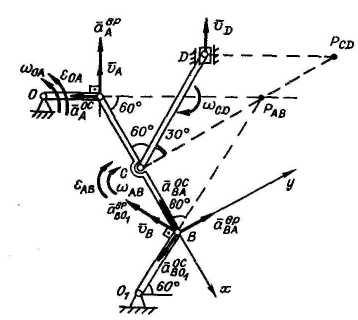
3). В заданном поло­жении механизма угловая скорость w_OA = 3 с^-1; угло­вое ускорение e_OA = 6 с^-2; OA = 0,6 м; AB = 1,2 м; CD = 1,4 м; O₁B = 0,4 м; AC = CB.

Найти v_B, v_D, w_AB, w_CD, ,a_B, e_AB.

Решение

Скорость точки A м/с.

МЦС звена AB – точка P_AB: м/с;МЦС звена CD – точка с^-1; м/с;м/с;с^-1; с^-1

Ускорение точки A

; м/с²; м/с².

Ускорение точки B ; ,или , гдем/с²; м/с²; . Проектируем (1) на оси х (||AB) и у (AB):

м/с²; м/с²; ;м/с²

Угловое ускорение звена AB с^-2.

Истинное направление e_AB показано на рисунке.

3.4 Сферическое движение

Это движение тела, при котором все точки движут­ся по сферам, общий центр которых совпадает с неподвижной точкой.

Положение тела в любой момент времени может быть задано тремя углами Эйлера: , ,  (, ,  - оси, связанные с телом):

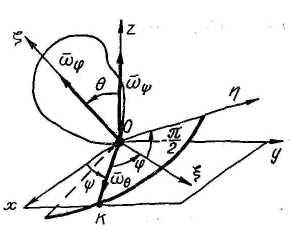
 - угол собственного вращения;

 - угол прецессии;

 - угол нутации.

(OK - линия узлов.)

Уравнения движения:

= (t),  =  (t),  =  (t).

Сферическое движение мож­но рассматривать как совокуп­ность последовательных беско­нечно малых поворотов вокруг мгновенных осей враще­ния, проходящих через неподвижную точку.

Кинематические характеристики тела:

- мгновенная угловая скорость (направлена вдоль мгновенной оси вращения);

- мгновенное угловое ускорение;

В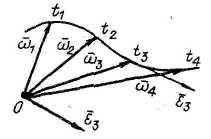екторнаправлен по касательной к годо­графу векторав рассматриваемый момент времени (аналогия: ).

Векторы ,принято отклады­вать от неподвижной точки тела.

Определение углового ускорения: представим в виде.

Где - орт мгновенной оси вращения;

 - алгебраическое значение угловой скорости.

Тогда

1. Если (ось неподвижна), то

2. Если  = const (вектор изменяется только по направлению). То

Где - угловая скорость вращения вектора .

(аналогия - приr = const.)

Скорости точек тела:

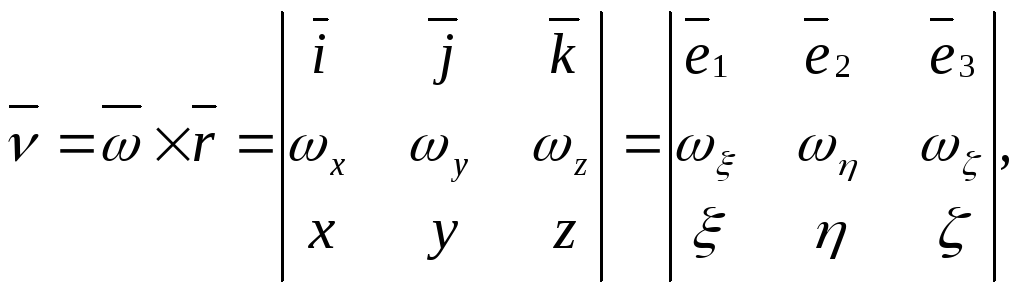
Где ,, орты неподвижной системы координат

x, у, z; - орты подвижной системы координат, , .

Ускорения точек тела:

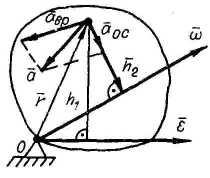Вращательное:

Осестремительное:

Модули

Пример

Ось OA, на которую свободно насажено тело 1, вра­щается вокруг вертикальной оси, имея в данный мо­мент угловую скорость ₁ = 1,6 с^-1 и угловое ускоре­ние e₁ = 2,8 с^-2.

Определить мгновенные угловую скорость и угловое ускорение тела 1, а также скорость и ускорение точки M, если тело 1 катится по неподвижному конусу 2 без скольжения; OK = 30 см; KM = 10 см.

Решение:

Тело 1 совершает сфериче­ское движение. Мгновенная ось вращения совпадает с линией касания тел 1 и 2 (OB).

1. Угловая скорость.

Имеем

г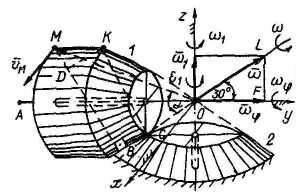де- угловая скорость вращения тела 1. Вокруг оси оа.

Вектор расположен на мгновенной оси вращения. Из треугольникаOFL находим

2. Скорость точки M.

Имеем

Вектор параллелен оси Ox.

Модуль скорости

Из треугольников МКО, ОМВ, МКД и ОСК находим

В результате

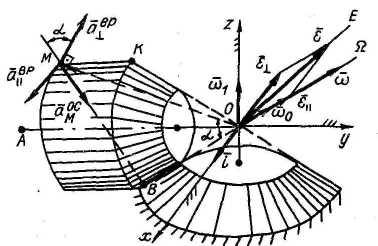
3. Угловое ускорение. Так как , где - орт мгновенной оси вращения,

где

Введем обозначения:

Где - орт оси.Ox.

Тогда

Так как и взаимно перпендикулярны, то

Учитывая, что

Получим

4. Ускорение точки M.

Имеем

Вектор осестремительного ускорения направлен по MB.

Модуль

Вращательное ускорение

Модули

Направления векторов и совпадают, а вектор расположен в плоскости yOz и перпендикулярен OM.

Модуль ускорения