8.3. Интервалы монотонности и экстремумы функции Краткая теория

1.Если производная функции y = f(x) положительна (отрицательна) во всех точках промежутка, то функцияy = f(x) монотонно возрастает (убывает)на этом промежутке.

2.Точкаx₀называется точкоймаксимума (минимума) функцииy = f(x), если существует интервал, содержащий точкуx₀, такой, что для всехxиз этого интервала имеет место неравенствоf(x₀)≥ f(x),(f(x₀)≤ f(x)). Точки максимума и точки минимума называются точкамиэкстремума.

3. Необходимое условие экстремума: в точке экстремума функции ее производная либо равна нулю(f ′(x)=0), либо не существует.

4.Первое достаточное условие экстремума: если в точке x₀функцияy = f(x) непрерывна, а производная f ′(x)при переходе через точкуx₀меняет знак, то точкаx₀– точка экстремума: максимума, если знак меняется с «+» на «-», и минимума, если с «–» на «+».

Если при переходе через точку x₀производная не меняет знак, то в точкеx₀экстремума нет.

5.Второе достаточное условие экстремума: если в точкеx₀ , а , тоx₀является точкой максимума функции. Если , а , тоx₀является точкой минимума функции.

6.Схема исследования функции на экстремум:

1) найти производную ;

2) найти критические точки функции, в которых производная равна нулю или не существует;

3) исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции;

4) найти экстремальные значения функции.

При исследовании функции на экстремум с помощью 2-го достаточного условия п. 1), 2), 4) сохраняются, а в п. 3) необходимо найти вторую производную и определить ее знак в каждой критической точке.

7.Чтобы найтинаибольшее и наименьшее значение(глобальный максимум и минимум) функции на отрезке [a,b] следует выбрать наибольшее (наименьшее) из значений функции в критических точках, находящихся в интервале (a,b) и на концах отрезка (в точкахaиb).

8.Если дифференцируемая на интервале (a,b) функция имеетединственнуюточку экстремума, то в этой точке достигается наибольшее или наименьшее значение (глобальный максимум или минимум) функции на интервале (a,b).

8.35. Найти интервалы монотонности и экстремумы функции.

Решение. В соответствии со схемой исследования (п. 6) найдем .Очевидно, производная существует при всех значенияхx. Приравниваяy′ к нулю, получаем уравнение откудаи- критические точки. Знаки производной имеют вид (рис. 8.1):

Рис. 8.1

На интервалах ипроизводная и функция возрастает, на интервалеи функция убывает;

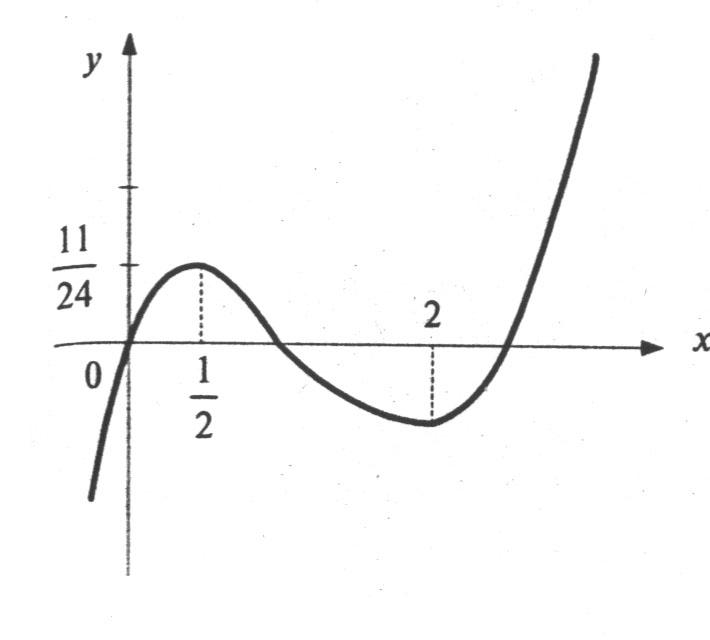
Рис. 8.2

- точка максимума и- точка минимума и, так как при переходе через эти точки производная меняет свой знак соответственно с «+» на «-» и с «-» на «+».

Замечание.Установить существование экстремума в критических точкахи, в которых можно было и с помощью второй производной (см. п. 5). Так как , а , то- точка максимума, а- точка минимума.

График данной функции схематично показан на рисунке 8.2.

8.36. Найти экстремумы и интервалы монотонности функции.

Решение..

Производная существует во всех точках, в которых существует и сама функция, т.е. при x> 0. Точки, в которых производная обращается в нуль, задаются равенствамиlnx=0,lnx-1 = 0, откудаx₁ =1,x₂ = е – критические точки. Знаки производной указаны на рис. 8.3.

Рис.8.3

Таким образом, функция монотонно возрастает на промежутках (0;1) и (е;+) и монотонно убывает на промежутке (1;е). Точкаx= 1 – точка максимума и, точка х = е – точка минимума и.

8.37. Найти экстремумы и интервалы монотонности функции

Решение.. Производная не существует приcosx=1 т.е. прии равна нулю при. Знак производной совпадает со знакомsin(x); таким образом у' >0 прииy'<0 при. Это, соответственно, интервалы возрастания и убывания функции.- точки максимума,- точки минимума.

8.38. Найти наибольшее значение (глобальный максимум) функциина интервале (10;18).

Решение. Найдем. На интервале (10;18) имеется всего одна критическая точкаx= 6. Производная при переходе через эту точку меняет знак с «+» на «-», т.е.x= 6 – точка максимума. Следовательно, функция достигает наибольшего значения приx= 16, т.е.. (Заметим, что наименьшего значения (глобального минимума) данной функции на указанном интервале не существует.)

8.40. Забором длиной 24 метра требуется огородить с трех сторон прямоугольный палисадник наибольшей площади. Найти размеры палисадника.

Решение.Пусть длины сторон палисадникаx,y. Тогда 2x+y= 24, т.е.y= 24-2x. Площадь палисадникаS=xy=x(24-2x) = 24x-2x², где 0<x<12 (ибо 24-2x>0). Таким образом, задача свелась к отысканию значенияx, при которомS(x) принимает наибольшее значение на интервале (0;12). НайдемS'(x) = 24-4x= 0 приx= 6. Легко видеть, чтоx= 6 – единственная точка экстремума – максимума функцииS(x). Это означает, что на интервале (0;12)S(x) принимает наибольшее значение приx= 6, т.е. искомые размеры палисадника 6 м и 24- 2 - 6 = 12 м.

Найти интервалы монотонности и экстремумы функции:

8.41..8.42..8.43..

8.44. .8.45. 8.46. .

8.47. .8.48..8.49..

8.50..8.51..8.52. .

8.53. .8.54. .8.55. .

8.56..8.57. .8.58. .

8.59..8.60..

Найти наибольшее и наименьшее значение (глобальный максимум и минимум) функции на отрезке [a,b]:

8.61.8.62.8.63.

8.64.8.65.8.66.

8.67.8.68.

Найти наибольшее или наименьшее значение (глобальный максимум или минимум) функции на интервале(a,b):

8.69.8.70.8.71.

8.72.8.73.8.74.

8.75. Рассматриваются всевозможные прямоугольные параллелепипеды, основания которых являются квадратами, а каждая из боковых сторон имеет периметр, равный 6 см. найти среди них параллелепипед с наибольшим объемом и найти этот объем.

8.76. Определить размеры открытого бассейна с квадратным дном, при которых на облицовку стен и дна пойдет наименьшее количество материала. Объем бассейнаVфиксирован.

8.77. Требуется огородить два участка: один в форме правильного треугольника, другой в форме полукруга. Длина изгороди фиксирована и равна Р. Определить размеры участков (сторону треугольника и радиус полукруга) так, чтобы сумма площадей этих участков была бы наименьшей.

8.78. В треугольнике с основаниемaи высотойh вписан прямоугольник, основание которого лежит на основании треугольника, а две вершины - на боковых сторонах. Найти наибольшую площадь вписанного прямоугольника.