5.Б. Приведение общих уравнений прямой к каноническому виду.

Пусть прямая линия задана общими уравнениями:

, (23)

где ,– нормальные векторы заданных плоскостей .

Выберем на прямой определенную точку . Для этого, например, зададим произвольно, а и получим из системы (23).

В качестве направляющего вектора возьмем вектор :

.

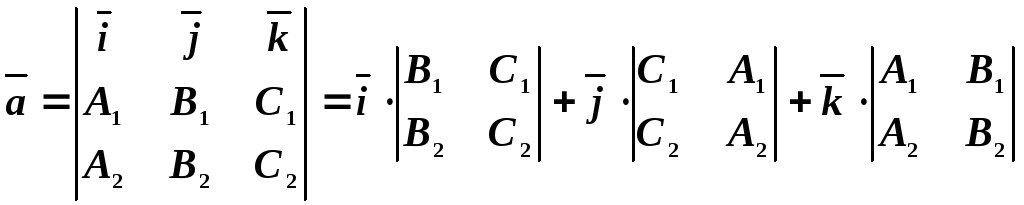Следовательно, каноническое уравнения прямой, соответствующее системе (23), имеет вид:

(24)

6. Угол между двумя прямыми. За угол между двумя прямыми

, ,

принимается угол между их направляющими векторами.

Здесь ,– направляющие вектора данных прямых:

(25)

Условие параллельности двух прямых:

(26)

Условие перпендикулярности двух прямых:

(27)

Пример 4. Составить каноническое уравнение прямой , проходящей через две заданные точки:,.

Согласно формуле (21) запишем:

.

Пример 5. Составить уравнение прямой , проходящей через точкупараллельно прямой:

Решение. На прямой образуем текущий вектор. Из канонического уравнения прямойнаходим направляющий вектор, здесь. Так как, тодля любой точки. Используя теперь условие параллельности, получаем канонические уравнения прямой:

.

Пример 6. Известны уравнения двух прямых:

: , и:

1. Проверить, являются ли ипараллельными.

2. Проверить, являются ли иперпендикулярными.

3. Найти угол между прямымии.

Решение.

а) Из условия параллельности прямых имеем, , если их направляющие вектораипараллельны. Координаты векторалегко получаются из заданных канонических уравнений прямой:. Для прямой, определяемой пересечением плоскостей, направляющий векторнаходится как векторное произведение:=, где,.

Вычисляем,

.

Так как координаты векторов ине пропорциональны, то условие параллельности для векторовине выполняется, а значит,не параллельна.

b) Из условия перпендикулярности прямых, , если. Так как, то условие перпендикулярности векторовине выполняется. Стало быть,не перпендикулярна к.

c) Угол между прямыми найдем по формуле (25):

.

Пример 7. Привести к каноническому виду уравнения прямой:

.

Решение.

Найдем направляющий вектор прямой :

.

За точку , через которую проходит искомая прямая в уравнении (20), можно принять точку пересечения ее с любой из координатных плоскостей, например с плоскостью. Так как при этом, то координатыопределяются из заданного уравнения прямой, если в нем положить:

.

Откуда находим ,и.

Итак, воспользовавшись теперь общей формулой (20), получаем:

.

7. Прямая и плоскость.

1. Угол между прямой и плоскостью.

Углом между прямой и плоскостью называется угол между прямой и ее проекцией на плоскость (рис. 11).

Пусть даны плоскость:c нормальным вектором и прямаяс направляющим вектором.

Угол между векторами иотличается от угла между прямой и плоскостью на;или

(28)

2) Условие параллельности прямой и плоскости:

(29)

3. Условие перпендикулярности прямой и плоскости:

(30)

Условие того, что прямая лежит в данной плоскости.

Пусть данная плоскость,

- каноническое уравнения прямой, проходящей через точку , параллельно вектору.

Условие принадлежности прямой плоскости имеет вид:

(31)

Если прямая лежит в плоскости, то она этой плоскости параллельна (первое уравнение) и любая точка прямой удовлетворяет уравнению плоскости (второе уравнение).