Тема 2.5. Геометрическое истолкование уравнений и неравенств между координатами. Алгебраические линии.

Уравнение линии на плоскости

Литература: [1], гл.4, § 1, стр. 67–68; [7], гл. 2, § 17, 18, стр. 62–68.

Основные определения, теоремы и формулы

Любое множество точек называется фигурой. Уравнение, неравенство или их система, которым удовлетворяют координаты любой точки фигурыFи не удовлетворяют координаты точки, не принадлежащей фигуреF, называетсяусловием, определяющим фигуру F.

Рекомендации к составлению уравнений фигур

При изучении геометрических объектов методом координат, часто рассматривают две задачи:

• по заданным геометрическим свойствам фигуры составить аналитические условия, определяющие эту фигуру (уравнение фигуры);

• по заданным аналитическим условиям, определить фигуру, выяснить ее геометрические свойства.

Чтобы составить уравнение фигуры необходимо:

1. выбрать систему координат, если она заранее не задана; при этом следует учесть, что если заданные и искомая фигуры характеризуются аффинными свойствами (т.е. характеризуются наличием общих точек, делением отрезков в заданном отношении и т. п.), то достаточно, выбрать аффинную систему координат; если же точки фигур характеризуются метрическими свойствами (т.е. расстоянием, величиной угла и т. п.), тонеобходимовыбрать прямоугольную или полярную системы координат; при выборе системы координат обратить внимание, в каком случае координаты заданных в условии задачи точек или координаты точек, определяющих заданные фигуры, вычисляются наиболее простым образом.

2. Взять произвольную точку фигуры и обозначить 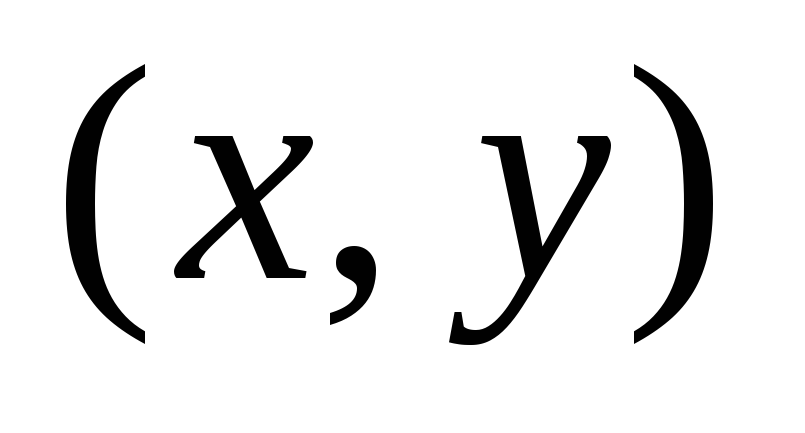или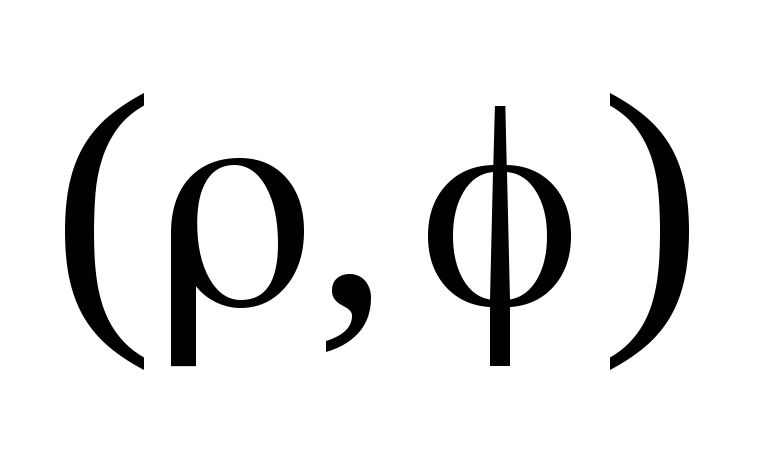ее координаты в выбранной системе координат.

3. Сформулировать необходимоеи достаточноеусловие принадлежности выбранной точки рассматриваемой фигуре; записать это условие символически. Если есть возможность, то записать это условие в векторной форме.

4. Записать сформулированное необходимое и достаточное условие принадлежности точки искомой фигуры в координатном виде.

Вопросы для самоконтроля

1. В чем суть метода координат в геометрии?

2. Что такое условие определяющее фигуру?

3. Как вывести уравнение некоторой фигуры? Приведите пример.

4. Какая линия называется алгебраической? Что такое уравнение линии? Можно ли в определении алгебраической линии аффинную систему координат заменить полярной?

5. Что такое порядок алгебраической линии? Поясните ответ на примерах.

6. Докажите, что порядок линии не зависит от выбора аффинной системы координат.

7. Выведите уравнение окружности в прямоугольной системе координат.

8. Докажите, что существуют неалгебраические линии.

Пример 1.Составить уравнение геометрического места точек плоскости, одинаково удаленных от осиОХи точкиВ(0, −2).

Решение.Из условия задачи видно, что на плоскости уже задана прямоугольная декартова система координатОХУ. ПустьМ(х,у) – точка искомого геометрического местаF. Согласно условию задачи имеем:

(расстояние от точки М(х,у)до осиОХесть абсолютная величина ее координаты).

Так как , то, подставляя это выражение в, мы получаем искомое уравнение фигурыF:. Возведя в квадрат обе части равенства, получим равносильное уравнение:. Значит, искомой фигуройFявляется парабола, заданная уравнением.

Пример 2.ТочкаМпри движении по плоскости все время удалена от точкиС на расстояние, равное. Найти уравнение траектории ее движения.

Решение 1.Введем на плоскости некую прямоугольную систему координатОХУ. Пустьи– координаты точкиС;х иу– текущие координаты точкиМв этой системе координат. Согласно условию задачи точкаМлежит на искомой кривой тогда и только тогда, когда. Так как,, или– искомое уравнение траектории движения точкиМ. Траектория движения точки представляет собой окружность радиусомr с центром в точкеC().

Р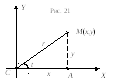ешение2.Введем на плоскости прямоугольную систему координатОХУтак, чтобы ее начало совпало с точкойС. Тогда в этой системе координат точкаСбудет иметь координаты (0, 0), текущие координаты точкиМобозначим (х,у). Искомое уравнение определиться условием, а так как, тои есть искомое уравнение в этой системе координат.

Решение 3.Введем на плоскости прямоугольную декартову систему координат так же, как и в предыдущем решении, и введем в рассмотрении параметрt,равной величине углаАСМ(Рис. 21). Выразим через параметр координатыхиу точкиМ:,, .

Полученные соотношения – параметрические уравнения траектории движения точки М(параметрические уравнения окружности радиусомrс центром в начале системы координат). Если из полученной системы уравнений исключить параметрt(для чего достаточно обе части уравнений возвести в квадрат и почленно сложить), то получим результат предыдущего решения, т. е..

Решение 4.Введем на плоскости полярную систему координатСРс полюсом в точкеС(Рис. 22).

Т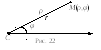очкаМудалена от точкиСна расстояниеr, если ее первая координатаравнаr(при любой второй координате). Тогда уравнение траектории движения точкиМможно записать так:.

Приведенные решения показывают, что одно и то же геометрическое место точек (одна и та же фигура) в разных системах координат записывается по-разному и выбор системы координат существенно влияет на простоту записи ее уравнения.

Пример 3. Даны точкиAиB. Доказать, что множество точек, из которых отрезокABвиден под прямым углом, есть окружность.

Решение. Искомая фигура определена метрическими свойствами точек, поэтому выберем прямоугольно-декартовую систему координат: за начало координат выберем точкуO– середину отрезкаAB, прямуюABвыберем за осьOX. Тогда выбранной системе координаты точек можно считать известными:A(, 0),B(−, 0). ПустьM(x,y) – произвольная точка плоскости. ТочкаMпринадлежит искомому множеству тогда и только тогда, когда. Записав это векторное равенство в координатной форме, получимилиПоследнее уравнение есть уравнение окружности с центром в середине отрезкаABи радиусом .

Задачи

1. Какие фигуры определяются в прямоугольной декартовой системе координат условиями:

1)x= −3; 2) ; 3) xy=0; 4) >1; 5)y=cos x; 6) ≤ 2; 7) xy=1;

8) ; 9) [x]=[y], где [z] – целая часть числаz.

Изобразить на чертеже прямоугольную декартову системе систему координат и каждую из этих фигур. Какие из рассматриваемых фигур являются алгебраическими? Определите порядок алгебраических линий.

2. Изобразить на чертеже множества точек, заданные системами неравенств:

1. x+1 > 0, y ≤ 2; 2) 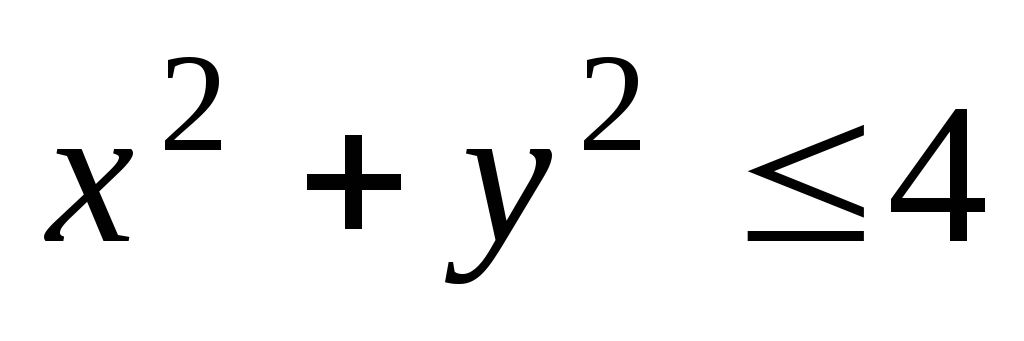, y ≥ 1; 3) y > sin x, y < cos x;

4) > 1, ≤ 2; 5),> 4.

3. Найти множество точек: 1) сумма квадратов расстояний от каждой из которых до двух заданных точек A иBпостоянна и равна положительному числу ; 2) разность квадратов расстояний от каждой из которых до двух заданных точекAиBпостоянна и равна положительному числу ;

3) для каждой из которых сумма расстояний до осей координат равна ;

4) для каждой из которых сумма квадратов расстояний до осей координат равна ;

5) сумма квадратов расстояний от которых до трех заданных точек A,BиC есть величина постоянная.

4. Концы отрезка длины 2а скользят по двум взаимно перпендикулярным прямым. Какую линию при этом описывает середина отрезка?

5. Доказать, что в любом четырехугольнике, противоположные стороны которого не параллельны, середины диагоналей и середина отрезка, концами которого являются точки пересечения прямых, содержащих противоположные стороны четырехугольника, лежат на одной прямой (теорема Гаусса).

Задачи повышенной трудности

1. На плоскости дана линия и точкаO. Через точкуO проводятся всевозможные прямые, на каждой из которых от точки пересечения с линией(если такая существует) откладывается в обе стороны отрезок, равный. Множество концов этих отрезков называетсяконхоидой кривой. Найти уравнение конхоиды прямой (конхоида Никомеда) в полярной системе координат, если полюс совпадает с точкой O, а полярная ось перпендикулярна данной прямой.

2. Найти множество всех точек плоскости, для каждой из которых отношение расстояний до двух данных точек AиB, больше данного числа.

3. Даны прямая и на ней две точки AиB. Две окружности переменных радиусов касаются этой прямой соответственно в точкаAиBи друг друга в точкеM. Какую фигуру образует множество точекM?