
terver_23-60
.pdf5Проверка статистических гипотез
5.1Постановка задачи
О проверке статистических гипотез я тоже рассказывал как об одной из главных задач статистики.
Статистической гипотезой будем называть любое предположение о виде теоретической функции распределения F (x) на основе наблюдения x1; x2; : : : ; xn. Таким образом, на основе выборки мы получаем некоторую информацию, основываясь на которой, можно анализировать теоретическое распределение, из которой получена выборка. Например, мы можем найти эмпирическую функцию распределения F и сопоставить какую-то теоретическую функцию F (x). В гипотезах мы предполагаем, что F (x) H, где H - некоторое множество функций распределений.
Гипотезы бывают (по простоте):
1.Простые. Такие гипотезы, в которых H = F . То есть в гипотезе мы предполагаем, что множество функций распределения из определения состоит из одного элемента. По сути, это проверка гипотезы, что выборка сделана из генеральной совокупности с однозначно заданной функцией распределения F (с фиксированными параметрами распределения). Например, гипотеза о том, что наблюдаемая случайная величина распределена по закону N(0; 1) (стандартизированному нормальному закону).
2.Сложные. Все остальные гипотезы, в которых мы предполагаем соответствие эмпирической функции распределения некоторому подмножеству функций распределения |H| > 1. Например, гипотеза о том, что наблюдаемая случайная величина распределена просто по нормальному закону N(a; ) (без заданных параметров a и ).
Гипотезы бывают (по виду):
1.Параметрические. В таких гипотезах требуется определить или ограничить некоторые параметры заданного семейства функции распределения. Например,
гипотеза о том, что наблюдаемая случайная величина распределена по нормальному закону N(a; ) с параметром a, находящимся в пределах от 0 до 3.
2.Непараметрические. В этих гипотезах необходимо определить само семейство функций распределений. Например, гипотеза о том что наблюдаемая величина распределена равномерно.
Гипотезы бывают (по типу):
1.Проверка согласия. Это гипотезы о согласованности эмпирической функции распределения, полученной на основе выборки, и некоторой заданной теоретической функцией распределения.
21

2.Проверка однородности. Гипотезы, в которых проверяется, что две или более выборок сделаны из одной генеральной совокупности (т.е. это выборки одной случайной величины).
3.Проверка независимости. Проверяется то, что данные выборки получены независимо друг от друга. Этот тип гипотез еще иногда называют гипотезы проверки стохастичности. На самом деле проверка стохастичности и независимости это не суть одно и то же (при проверке стохастичности данные могут быть и зависимы), но граница между ними довольно зыбкая.
Различают 2 непересекающиеся гипотезы: H0 - основная (нулевая) гипотеза и H1 - альтернативная (конкурирующая) гипотеза. H1 = H0
Статистический критерий - некоторое правило, которое позволяет, основываясь на данных только выборки, принять или опровергнуть нулевую гипотезу. Формально: f : (x1; x2; : : : ; xn) → {H0; H1}.
Зам. Иногда различают большее число гипотез, (например, несколько альтернативных). В таком случае критерий будет действовать похожим образом:
f : (x1; x2; : : : ; xn) → {H0; H1; : : : ; Hk}
Зам. К критериям порой применяют ту же классификацию, что и к гипотезам. То есть различают параметрические и непараметрические критерии, критерии согласия/однородности/независимости. Под этим подразумевается, что данные критерии предназначены для проверки гипотез указанного типа.
Зам. ! Если критерий выполняется, то нельзя говорить о том что гипотеза доказана, доказать ее основываясь на статистических данных невозможно (мы всегда работаем с вероятностями < 1). Обычно при выполнении/невыполнении критерия приводится следующая формулировка "гипотеза не противоречит/противоречит опытным данным". Коротко обычно говорят "гипотеза принимается"или "гипотеза отвергается".
5.2Ошибки первого и второго рода
Будем работать со случаем двух гипотез - основной и альтернативной.
Критическая область критерия (!k). Можно считать что выборка - элемент n-мерного пространства вещественных чисел: (x1; x2; : : : ; xn) Rn. Тогда !k Rn и (x1; x2; : : : ; xn) !k, то H0 отвергается (!k такое подмножество n-мерного пространства, на котором основная гипотеза отвергается). ! = Rn\!k - область допустимых значений.
Опыт
H0 H0
R0
Жизнь R0 ′
22
R0 - в реальности гипотеза верна, R1 - неверна.
Ошибка первого рода = P ((x1; x2; : : : ; xn) !k|R0) или = P (H1|R0). Ее еще называют значимостью критерия. Это вероятность отвергнуть верную гипотезу.
Ошибка второго рода = P ((x1; x2; : : : ; xn) ! |R1) = P (H0|R1). Ее еще называют оперативностью критерия. Это вероятность принять неверную гипотезу.
Пример H0 - есть аппендицит. H1 - нет аппендицита. Ошибка первого рода - вероятность не провести операцию, когда есть заболевание. Ошибка второго рода - вероятность провести операцию, когда заболевания нет. В каждой конкретной ситуации надо решать, какая ошибка "лучше".
Мощность критерия. ′ = P ((x1; x2; : : : ; xn) !k|R1) = P (H1|R1). Это вероятность отвергнуть неверную гипотезу (хороший вариант). ′ = 1 −
Надежность критерия. = P ((x1; x2; : : : ; xn) ! |R0) = P (H0|R0). Это вероятность принять верную гипотезу (тоже хороший вариант). = 1 −
C помощью этих параметров можно задавать критические области критериев. Это напоминает то, как мы, задавая надежность , получали доверительный интервал. Однако тут ситуация чуть сложнее. Нам хочется, чтобы и ошибка первого и ошибка второго рода были как можно меньше. Однако уменьшение ошибки первого рода влечет за собой уменьшение критической области !k. Уменьшение же ошибки второго рода влечет за собой уменьшение области допустимых значений ! , что влечет за собой увеличение !k и приводит к парадоксу. Следовательно надо искать гармоничный вариант. Обычно задается и на ее основе ищется !k.
Заметим, что задача поиска !k довольна сложна, т.к. это область в n-мерном пространстве. Поэтому зачастую критерии работают не с областью n-мерного пространства !k, а с некоторой областью одномерного пространства dk, и на основе выборки строят некоторое число S = S(x1; x2; : : : ; xn) R, которое называют статистикой критерия. Собственно, в таком варианте мы проверяем попадает ли статистика в заданную критическую область. Если попадает - то гипотеза отвергается. То есть мы переходим от задачи в n-мерном пространстве проверки: (x1; x2; : : : ; xn) !k к задаче в одномерном пространстве: S(x1; x2; : : : ; xn) dk. Далее будем границы критических областей обозначать индексом 0: d0. Различают односторонние и двусторонние критические области. Нарисовать примеры областей (односторонняя, двусторонняя внутренняя, двусторонняя внешняя).
Зам. Необходимо четко различать гипотезу, критерий, статистику критерия и критическую область. Гипотеза - это предположение, критерий - правило или метод, по которому это предположение проверяется. Статистика - число или диапазон, которые вычисляются в критерии. Критические области критериев определены и обычно различаются только от размера выборок, которые определяют степени свободы. Статистика вычисляется на основании данных выборки и, в случае попадания ее в критическую область, критерий дает отрицательный результат и гипотеза отвергается.
Общий алгоритм проверки гипотезы:
23

1.Выбирается критерий, задается надежность (или значимость) критерия. Надежность должна быть около 1, значимость - около 0.
2.Находится статистика критерия - число из R.
3.На основе надежности строится критическая область (т.е. находятся одно или 2 граничных числа).
4.Проверяется, попадает ли статистика в критическую область. Если попадает - гипотеза отвергается, если нет - принимается.
5.3Основные критерии
Очень большой объем информации по проверке стат.гипотез есть в учебнике: Кобзарь Л.И. "Прикладная математическая статистика".
Задача |
Название |
Статистика |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Критическая область |
|||||||||||||||||||
|
|
|
|
|
= |
√ |
|
|
|
max |
|
) | |
F (x) |
− |
F (x) |
| |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Критерий со- |
n |
x |
|
Если > 0, то H0 отвергает- |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
( |
; |
∞ |
|
|
|
|
0 |
|
||||||||||||||||||||||||
|
гласия |
Кол- |
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
ся. 0 - квантиль распределе- |
|||||||||||||||
|
(учитывается максимальное от- |
|||||||||||||||||||||||||||||||||||||
Согласие |
могорова |
клонение) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ния Колмогорова |
||||||||||||||||||
|
Критерий |
n!2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
||||
|
!2 |
Крамера- |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Мизеса |
(ин- |
n |
(F (x) − F0(x)) |
dF0 |
(x) |
|
|
|
|
Если n!2 > n!02 H0 отвергает- |
|||||||||||||||||||||||||||
|
тегральный |
−∞ |
|
|
|
|
|
|
|
|
|
|
|
отклонение |
|
|
на |
2 |
- табличное значение |
|||||||||||||||||||
|
(учитывается∫ |
|
|
|
ся. n!0 |
|||||||||||||||||||||||||||||||||
|
критерий) |
всей области) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
2 = |
r |
(nk − npk)2 |
, r - ко- |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
k=1 |
|
|
|
|
npk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
интервалов разбиения, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
личество∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
Пирсона |
nk - |
количество |
элементов |
|
|
вы- |
Если 2 |
> 0(r−1) H0 отверга- |
|||||||||||||||||||||||||||
|
|
борки в |
|
k-ом |
|
диапазоне. |
pk |
ется. 0 |
- квантиль хи-квадрат |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
с r-1 степенью свободы |
|||||||||||||||||||||||||||||||
|
|
|
|
|
- вероятность попадания в k- |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
ый |
интервал, |
|
основываясь |
на |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
теор.распределении. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Критерий |
Аналогичен критерию Колмого- |
Если > 0, то H0 отвергает- |
|||||||||||||||||||||||||||||||||||
|
рова для согласия, но анализи- |
|||||||||||||||||||||||||||||||||||||
Критерий |
Колмогорова- |
руются 2 эмпирические функции |
ся. 0 - квантиль распределе- |
|||||||||||||||||||||||||||||||||||
однород- |
Смирнова |
= √ |
|
|
nm |
|
|
max |F1 (x) − F2 (x)| |
ния Колмогорова |
|||||||||||||||||||||||||||||
ности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
n + m |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
x1; x2; : : : ; xn; y1; y2; : : : ; ym Пусть |
Двусторонняя критическая об- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ласть на основе статистики |
|||||||||
|
Критерий |
n<m. Тогда zi = xi − yi, i = 1; n. |
||||||||||||||||||||||||||||||||||||
двух вы- |
Фишера. Если 0 < < |
|
, то |
|||||||||||||||||||||||||||||||||||
0 |
||||||||||||||||||||||||||||||||||||||
борок |
знаков |
|
Статистика - количество поло- |
H0 отвергается. |
|
|
0 и |
|
- кван- |
|||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
0 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
жительных разностей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
тили распределения Фишера. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
24

|
Критерий |
x1; x2; : : : ; xn; y1; y2; : : : ; ym Пусть |
|
|
u − M[u] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
Манна- |
n<m. Статистика |
|
|
|
|
n |
zij, |
|
|
|
|
N(0; 1) |
|
|
|
|
|||||||||||||||||||||||
|
u |
= |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
D[u] |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Уитни |
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
√ |
|
|
|
nm |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
если xi |
|
|
|
|
|
i;j∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
(ранговый |
|
|
0; |
|
< yj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
критерий) |
zij = {1; |
если xi |
|
≥ yj . |
|
|
|
|
|
M[u] = |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Критерий |
R1 - сумма рангов 1ой выборки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
R2 - сумма рангов 2ой выборки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Уилкоксона |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ранговый |
|
|
|
|
|
|
|
|
n + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
критерий, |
!1 = nm + n( |
|
|
|
|
|
) − R1 |
|
D[u] = nm |
(n + m |
− |
1) |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
модифика- |
|
|
|
|
|
|
|
|
m + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
ция Манна- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
!2 = nm + m( |
|
|
|
|
|
|
) − R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Уитни) |
u = min(!1; !2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для |
|
сравнений |
|
используют |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
таблицы или |
|
|
приведение |
к |
|
|
|
||||||||||||||
|
Критерий |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
стандартному |
|
|
нормальному |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
распределению. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Сэвиджа |
n |
|
n+m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
(ранговый, |
∑ |
|
∑ |
|
|
|
1 |
Ri - ранг i-го |
|
S − M[S] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
S = |
|
|
|
|
|
|
|
|
|
|
|
|
N(0; 1) |
|
|
|
|
||||||||||||||||||||||
|
только для |
i=1 j=n+m+1−Ri |
|
j |
|
|
|
|
|
|
|
|
|
D[S] |
|
|
|
|
|
|
||||||||||||||||||||
|
положи- |
элемента 1-ой выборки в объеди- |
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
ненной выборке. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
тельной |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M[S] = min(n; m) |
|
|
|
|
|
|
|||||||||||||
|
выборки) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nm |
|
|
|
|
|
|
|
1 |
|
n+m |
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D[S] = n + m |
− |
1 |
|
(1−n + m |
|
j ) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 = 4 |
|
k |
1 |
mi2 − N |
|
если |
2 > 02(k |
|
− |
1) (кван- |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
Медианный |
|
=1 |
|
n |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Критерий |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
критерий |
|
|
|
|
∑i |
|
|
|
|
|
|
|
|
|
|
тиль хи-квадрат), то гипотеза |
|
|
|
|||||||||||||||||||||
однород- |
mi - число элементов i-ой выбор- |
отвергается |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
ности |
|
ки, больших чем медиана объ- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
несколь- |
|
единенной выборки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ких (k) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выборок |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ri - сумма рангов i-ой выборки в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Критерий |
объединенной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
∑i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Краскела- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Уоллиса |
|
2 |
= |
|
|
Ri |
|
− |
n(n + 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
=1 |
|
ni |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25

|
|
|
Объединенная выборка делится |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
на r отрезков. nij - количество |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
элементов i-ой выборки, попав- |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
ших в j-ый интервал. |
|
если 2 > 02(k−1)(r−1) (кван- |
|
||||||||||||||||||
|
|
Критерий |
|
|
|
|
|
∑ |
2 |
|
|
|
||||||||||||
|
|
однородно- |
|
|
2 |
|
|
nij |
|
тиль хи-квадрат), то гипотеза |
|
|||||||||||||
|
|
сти 2 |
|
|
|
= n |
( i;j |
|
) |
|
отвергается |
|
|
|
|
|
|
|||||||
|
|
|
ni:n:j |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
ni: - сумма элементов i-ой стро- |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
ки, n:j - сумма элементов j-го |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
столбца |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lm - медиана. Ставим вместо эле- |
|
u − M[u] |
|
|
N(0; 1) |
|
|||||||||||||||
|
|
|
мента выборки +, если он боль- |
|
√D[u] |
|
|
|
|
|
||||||||||||||
|
|
Критерий се- |
ше медианы и -, если он мень- |
|
2n1n2 |
|
||||||||||||||||||
Критерий |
рий |
ше. Число подряд стоящих плю- |
M[u] = |
|
|
|
+ 1 |
|
||||||||||||||||
n1 + n2 |
|
|||||||||||||||||||||||
незави- |
|
сов или минусов называем сери- |
|
|
2n1n2 |
|
|
2n1n2 − (n1 + n2) |
|
|||||||||||||||
симости |
|
ей. Статистика N - число серий. |
D[u] = |
|
|
|
||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
и |
стоха- |
|
n1, n2 - число + и - |
|
|
|
|
|
n1 + n2 |
|
|
|
n1 + n2 − 1 |
|
||||||||||
стично- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сти |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составляем |
таблицу: строки - |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
значения 1го признака, столб- |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
цы - значения 2го признака. nij- |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
количество пар (i,j) |
|
Если 2 > 02(m1 − 1)(m2 − 1) |
|
||||||||||||||||||
Критерий |
Критерий 2 |
|
|
|
m1 |
m2 |
|
n |
n |
|
|
|||||||||||||
|
|
|
|
|
|
∑∑ |
( |
2 |
H0 отвергается. |
|
|
|
||||||||||||
незави- |
|
2 = |
|
|
ij − ˜ij) |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
n˜ij |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
симости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
i=1 j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2х |
кач. |
|
|
ni:n:j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
призна- |
|
n˜ij = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ков |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5.4Критерии Колмогорова
В критериях Колмогорова(согласия) и Колмогорова-Смирнова(однородности) статистика считается через максимальную разницу функций распределения. На практике есть смысл проверять отклонения только в точках перелома (нарисовать 2 графика и показать). В итоге для критерия согласия применяется следующая формула для статистики:
= √ |
|
max [ |
|
|
|
− |
2i − 1 |
| |
|
1 |
|
||||
n |
F |
(x |
) |
+ |
] |
||||||||||
2n |
2n |
||||||||||||||
|
|
i 1 |
≤ |
n |
| |
0 |
i |
|
|
|
|||||
|
|
≤ |
|
|
|
|
|
|
|
|
|
|
|
||
Формула для функции распределения Колмогорова: F (x) = ∑∞ (−1)ke−2k2z2 . На прак-
−∞
тике для поиска квантилей используются таблицы. Для критерия однородности име-
26

ем: |
|
|
|
|
|
|
|
|
|
0; |
если x < x1(n) |
0; |
если x < y1(m) |
||||
F1 (x) = nk ; |
если xk(n) < x < xk(n+1) |
F2 (x) = |
k |
; |
если yk(m) < x < yk(m+1) |
|||
m |
||||||||
|
|
|
(n) |
|
|
(m) |
||
|
|
если |
|
если |
||||
|
|
x > xn |
|
x > ym |
||||
1; |
|
1; |
|
|||||
У нас есть точки перелома по функции F1 (x) и по функции F2 (x). Однако видно, что можно рассматривать максимум отклонения только по одним из этих точек перегиба.
Имеем: |
D−(n; m) = max |
|
i |
|
|
|
F (x ) |
= max |
|
|
F (y |
) |
|
j−1 |
|
|||||||||||||||||
|n |
− |
| |
− |
| |
||||||||||||||||||||||||||||
|
1 |
|
i |
n |
|
2 |
i | |
|
1 |
j |
≤ |
m |
1 |
j |
|
m |
||||||||||||||||
|
|
|
|
≤ ≤ |
|
|
|
|
|
|
|
|
|
|
|
|
≤ |
|
|
|
|
|
|
|
|
|
|
|
||||
D+(n; m) = max |
|
F |
(x |
) |
|
|
i−1 |
|
= max |
|
j |
|
|
|
F (y ) |
|. |
|
|||||||||||||||
| |
− |
| |
|m |
− |
|
|||||||||||||||||||||||||||
|
1 |
i |
n |
2 |
|
|
i |
|
n |
|
1 |
j |
≤ |
m |
1 |
|
j |
|
||||||||||||||
|
|
≤ ≤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≤ |
|
|
|
|
|
|
|
|
|
|
|
|
||
Зам. Главный недостаток критериев Колмогорова: чувствительность к скачку.
5.5Критерий Мизеса
В нем также на практике ищется не интеграл по всей области, а сумму отклонений
в точках перелома:
n!2 = ∑n [|F0(xi) − 2i2−n 1| + 121n]
i=1
На практике для поиска квантилей используются таблицы распределения n!2.
5.6Критерии 2
Для критерия согласия нужно помнить о следующем: Во-первых, диапазоны разбиения выбираются так, чтобы npk ≥ 5. При меньшем нельзя гарантировать надежности метода. Интервалы здесь не обязательно брать равными, если у интервала неравенство нарушается, его можно объединить с соседним. Второе: pk в методе - теоретическая вероятность, нельзя брать вместо нее частоту, это самая распространенная ошибка, приводящая к тому, что оценка равна 0.Надо брать pk = F (ak) − F (ak−1). Третье: если теоретическое распределение задано нечетко, то можно заменять параметры распределения его оценками. В таком случае это будет уже параметрический критерий, и необходимо сравнивать статистику с 20(r − l − 1), где l - количество параметров распределения.
Зам. (к критерию 2 о независимости). По сути дела его можно применять и для количественных выборок. В этом случае вместо конкретных значений случайных величин будем брать интервалы, и подсчитывать количество пар, попадающих в соответствующие интервалы по x или y. То есть выборка X разбивается на r диапазонов [a1; : : : ; ar], выборка У разбивается на s диапазонов [b1; : : : ; bs]. Тогда nij - количество пар (x,y), в которых x ai, y bj. В остальном метод идентичен.
27
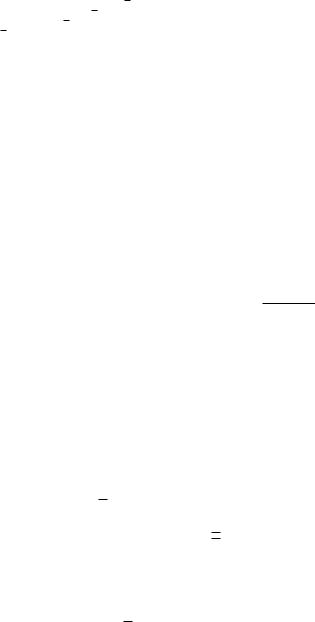
5.7Критерий знаков
В критерии знаков надо проверять, что количество отрицательных/положительных знаков распределено по биномиальному закону (схеме Бернулли) с параметром 1/2. P (zi < 0) = P (zi < 0) = 12 . Задается c и c квантили биномиальной схемы порядка. Можно показать, что c = n − c
5.8Общие рекомендации к применению критериев согласия
Зачастую в критерии согласия необходимо сравнивать эмпирическое распределение с некоторым семейством теоретических распределений: например, с нормальным распределение без заданных параметров a и . Как написано выше, в таком случае надо заменять параметры распределения их оценками. Рассмотрим примеры оценивания параметров самых распространенных распределений тервера:
1.Равномерное распределение. У равномерного распределения есть 2 параметра: a и b - начало и конец интервала, на которых оно задано. Нам нужно построить их оценки. Можно воспользоваться методом моментов, который мы
описывали в главе 2. Известно, что M = |
a + b |
и D = |
(b − a)2 |
. Следователь- |
|
12 |
|||
2 |
|
|
||
но, если мы найдем оценки математического ожидания и дисперсии, то заменив в написанной выше системе параметры их оценками, мы можем найти a и b. Второй способ проще, хотя для него нельзя гарантировать состоятельности и эффективности оценок. a и b - концы диапазона, в котором содержится распределение случайной величины, то есть в котором содержатся все ее значения. Поэтому для выборки можно взять a = xmin и b = xmax.
2.Показательное распределение. У показательного распределения 1 пара-
метр распределения: . Для него очень просто оценка находится по методу
моментов, вспомнив что M[X] = 1 . Следовательно, заменив матожидание выборочным средним, можно оценить через = x1
3.Нормальное распределение. У нормального распределения 2 параметра распределения: a и . Если вспомнить, что a совпадает с математическим ожиданием, а с среднеквадратическим отклонением, опять легко можно применить метод моментов. Получим a = x, a = m2
28

6Корреляционный анализ
6.1Постановка задачи
В этой главе мы во многом будем работать с понятиями теории вероятностей, но в курсе статистики нас интересует анализ зависимости случайных величин на основе опытных данных. Основной задачей корреляционного анализа является выявление связи между случайными величинами в количественной форме. Это значит, что мы должны найти некоторое число/коэффициент, выражающе взаимосвязь случайных величин. Например, зависимость между случайными величинами роста и веса некоторой выборки людей. Взаимосвязь между ними определенно есть, но не факт что сильная. Поэтому правильнее не просто говорить "есть взаимосвязь"или "нет взаимосвязи но определять коэффициент этой связи. Напомним, что в тервере если случайные величины независимы, то F (x; y) = F (x)F (y), в случае зависимости равенство имеет следующий вид: F (x; y) = F (x)F (y|x) = F (y)F (x|y). В статистике при корреляционном анализе мы работаем с двумерной выборкой:
(x1; y1); (x2; y2); : : : ; (xn; yn). Это все равно что взять 2 выборки x1; x2; : : : ; xn и y1; y2; : : : ; ym
одинакового размера. Для определения количественной связи вводят коэффициенты корреляции.
6.2Коэффициент корреляции
Напомним, что в тервере коэффициент корреляции имел следующий вид: rxy = M[(x − M[x])(y − M[y])]. В статистике нас интересует его оценка. Возьмем двумер-
ную выборку (x1; y1); (x2; y2); : : : ; (xn; yn). Оценка коэффициента корреляции (или выборочный коэффициент корреляции) как и большинство оценок получается из формулы самого параметра заменой параметров тервера на их оценки:
∑n
|
|
|
|
|
i=1 (xi − |
x |
)(yi − |
y |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
rxy = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
√i=1 (xi − x)2 i=1 (yi − y)2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
∑ |
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
. При малом (n<15) объеме выборки лучшей оценкой принимается |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
r |
= r |
1 + 1 − (r )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
xy |
( |
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2(n − 3) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
В связи с корреляцией обычно говорят про ковариацию: |
C |
|
= M x |
M |
x |
|
|
y |
|
||||||||||||||||||||
|
xy |
n |
[( − |
[ |
|
])( |
|
|
− |
||||||||||||||||||||
M[y])] = M[xy]−M[x]M[y]. Тогда ее оценка следующая: mxy = n1 |
i=1 (xi − |
|
)(yi − |
|
) = |
||||||||||||||||||||||||
x |
y |
||||||||||||||||||||||||||||
1 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
n i=1 xiyi −xy. По сути ковариация - это ненормированная корреляция, и выборочную |
|||||||||||||||||||||||||||||
∑ |
|
|
|
|
mxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
корреляцию можно записать как rxy = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
mxmy |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
√
Свойства коэффициента корреляции:
29
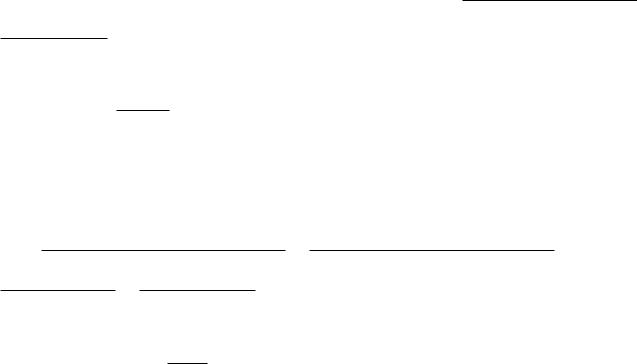
1. rxy = 0, если x и y независимы. В обратную сторону неверно, кроме случая нормального распределения.
2. rxy = 1, если x и y зависимы. Если коэффициент равен 1, то взаимосвязь прямая, если -1 то обратная.
3. rxy = ryx. Это следует напрямую из определения корреляции.
4. |
rxx = 1. Действительно, исходя из определения корреляции rxx = |
M[(x − M[x])(x − M[x])] |
= |
|||||||||||
|
|
M[(x − M[x])2] |
|
|
|
D[x] |
|
|
x x |
|||||
|
|
|
= |
= 1 |
|
|
||||||||
|
|
|
|
|
|
|
||||||||
|
|
x2 |
|
|
|
|
|
|
D[x] |
|
|
|
|
|
5. |
|rxy| ≤ 1. Можно показать, что Cxy2 ≤ D[x]D[y]. Тогда |Cxy| ≤ [x] [y]. rxy = |
|||||||||||||
|
|
Cxy |
|
r |
|
= |
|
|Cxy| |
|
1 |
|
|
||
|
|
[x] [y]. |
xy| |
[x] [y] ≤ |
|
|
||||||||
|
|
| |
|
|
|
|
|
|
||||||
6.|rxy| = 1, если y = kx + b. То есть, корреляция равна 1, если существует линейная зависимость между y от x. Естественно в этом случае будет и обратная линейная зависимость x от y.
Доказательство.
rxy = |
M[(x − M[x])(kx + b − M[kx + b])] |
= |
M[(x − M[x])(kx + b − kM[x] − b)] |
= |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x y |
|
|
|
|
|
|
|
x y |
||||
|
M[k(x − M[x])2] |
= |
|
kM[(x − M[x])2] |
= |
kD[x] |
|
|||||||||||||||
|
|
|
|
|
|
x y |
||||||||||||||||
|
|
|
|
x y |
|
|
|
|
|
x y |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
= D[y] = D |
kx |
b = k2D x |
|
|
|
k |
||||||||||||||
|
|
y |
√ |
√ [ |
|
|
+kD] [x]√ |
[ |
|
] = | | x |
||||||||||||
В итоге получим rxy = |k| x2 = ±1 и rxy = 1
В итоге мы имеем, что −1 ≥ rxy ≤ 1. Для оценок эти свойства должны тоже вы-
полняться в пределе. |
| |
rxy |
| ≤ |
1. rxy |
−−−→ |
0, если независимы. |
| |
rxy |
| −−−→ |
1, если есть |
||
|
|
|
|
|
|
|||||||
|
|
|
|
|
n |
→∞ |
|
|
|
n |
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
||
линейная связь
6.3Корреляционная матрица
Пусть у нас есть несколько случайных величин (больше 2). Для них можно составить корреляционную матрицу - матрицу попарных корреляций. То есть имеем X1; X2; : : : ; Xn - случайные величины. Будем обозначать rij = rXi;Xj . Тогда корреляционная матрица будет следующего вида:
r11 r12
r21 r22
Kx = ..
. : : :
rn1 rn2
Свойства корреляционной матрицы:
: : : r1n
: : : r2n
: : : ...
: : : rnn
30
