1) , 2), 3), 4).

 Выясним, каким образом они интегрируются.

1)

2)

Вычислить интеграл .

Решение.

Разложим подынтегральное выражение на простейшие дроби:

     

Сгруппируем слагаемые и приравняем коэффициенты при членах с одинаковыми степенями:

     

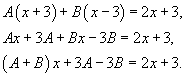
Следовательно,

     

Тогда

     

Теперь легко вычислить исходный интеграл

     

24. Основные методы интегрирования.

I. Метод непосредственного интегрирования

Задача нахождения неопределенных интегралов от многих функций решается методом сведения их к одному из табличных интегралов.

Пример 1.

∫(1-√x)²dx=∫(1-2√x+x)dx=∫dx-∫2√xdx+∫xdx=∫dx-2∫xdx+∫xdx=

II. Метод подстановки (интегрирование заменой переменной)

Если функция x=φ(t) имеет непрерывную производную, то в данном неопределенном интеграле ∫f(x)dx всегда можно перейти к новой переменной t по формуле

∫f(x)dx=∫f(φ(t))φ'(t)dt

Затем найти интеграл из правой части и вернуться к исходной переменной. При этом, интеграл стоящий в правой части данного равенства может оказаться проще интеграла, стоящего в левой части этого равенства, или даже табличным. Такой способ нахождения интеграла называется методом замены переменной.

Пример 7. ∫x√x-5dx

Чтобы избавиться от корня, полагаем √x-5=t. Отсюда x=t²+5 и, следовательно, dx=2tdt. Производя подстановку, последовательно имеем:

∫x√x-5dx=∫(t²+5)•2tdt=∫(2t⁴+10t²)dt=2∫t⁴dt+10∫t²dt=

III. Метод интегрирования по частям

Метод интегрирование по частям основан на следующей формуле:

∫udv=uv-∫vdu

где u(x),v(x) –непрерывно дифференцируемые функции. Формула называется формулой интегрирования по частям. Данная формула показывает, что интеграл ∫udv приводит к интегралу ∫vdu, который может оказаться более простым, чем исходный, или даже табличным.

Пример 12. Найти неопределенный интеграл ∫xe^-2xdx

Воспользуемся методом интегрирование по частям. Положим u=x, dv=e^-2xdx. Тогда du=dx, v=∫xe^-2xdx=-e^-2x+C Следовательно по формуле имеем: ∫xe^-2xdx=x(-e^-2x)-∫-^-2dx=-e^-2x-e^-2x+C

25. Определённый интеграл. Геометрические и основные свойства.

Определённый интеграл - Проще говоря, этоинтеграл, численно равный площади части графика функции в пределах от a до b, т. е. площади криволинейной трапеции.

Определенный интеграл обозначается символом . Егоможно найти по формуле Ньютона — Лейбница:

Свойства

Чтобы функция была интегрирована по Риману, необходимо и достаточно, чтобы она была ограниченной.

Геометрический смысл

Определённый интеграл как площадь фигуры

Определённый интеграл численно равен площади фигуры, ограниченной осью абсцисс, прямымиии графиком функции.

26. Приложение определённого интеграла.

Объём тела вращения. Рассмотрим тело, полученное вращением вокруг оси OX  криволинейной трапеции, ограниченной графиком функции  f ( x ), прямыми  x = a  и  x = b и осью  OX  (рис.10 ).

 

Объём  V тела вращения будет равен:

Работа переменной силы. Рассмотрим движение материальной точки вдоль оси  OX под действием переменной силы  f , зависящей от положения точки  x на оси, т.e. силы, являющейся функцией  x. Тогда работа  A, необходимая

для перемещения материальной точки из позиции  x = a  в позицию  x=bвычисляется по формуле: