Основные свойства неопределённого интеграла

Если функция  f ( x ) имеет первообразную на промежутке  X, и  k – число, то

Короче: постоянную можно выносить за знак интеграла.

Если функции  f ( x )  и  g ( x ) имеют первообразные на промежутке  X , то

Короче: интеграл суммы равен сумме интегралов.

Если функция  f ( x ) имеет первообразную на промежутке X , то для внутренних точек этого промежутка:

 

Короче: производная от интеграла равна подынтегральной функции.

 

Если  функция  f ( x )  непрерывна на промежутке  X  и дифференцируема во внутренних точках этого промежутка, то:

Короче: интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования

21. Таблица интегралов.

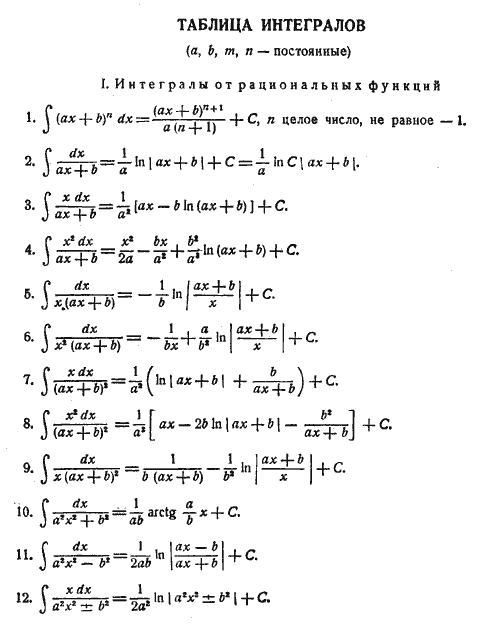
22. Формулы интегрирования по частям и её вывод.

Пусть надо вычислить интеграл вида

∫  U(x) · v(x) dx ,

где   v(x)  имеет очевидную первообразную   V(x).

Тогда

∫  U(x) · v(x) dx   =   ∫  U(x) · V'(x) dx   =   ∫  U(x)  dV(x) .

Такого рода преобразование называется подведением под знак дифференциала, поскольку функция v(x) исчезает в интегрируемом выражении и появляется под знаком дифференциала в виде своей первообразной V(x).

Если функция U(x) выражается через функцию V(x) по некоторой формуле U(x) = w(V(x)), то

∫  U(x)  dV(x)   =   ∫  w(V(x)) dV(x)   =   ∫  w(t) dt ,

где t = V(x). Таким образом отыскание исходного интеграла сводится к отысканию интеграла

∫  w(t) dt

В нем функция t = V(x) выступает как независимая переменная, т.е. произошла замена переменной.

Если функция U(x) не выражается через функцию V(x) по некоторой формуле U(x) = w(V(x)), то может оказаться полезным преобразование, называемое интегрированием по частям. Оно определяется следующей теоремой.

Теорема 1. Пусть функции U(x) и V(x) дифференцируемы на некотором интервале и на этом интервале существует интеграл   ∫ V(x)U '(x)  dx .

Тогда существует интеграл   ∫ U(x)V '(x)  dx и справедлива формула

∫ U(x)V '(x)  dx   =   U(x)V(x)   −   ∫ U '(x)V(x)  dx.

(1)

Доказательство следует из формулы дифференцирования произведения. Оно приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 168.

Замечание 1. Очевидно, что в формуле интегрирования по частям оператор дифференцирования, обозначенный штрихом, перемещается с V на U. Этим обусловлена важная роль формулы при доказательстве самосопряженности линейных дифференциальных операторов.

Замечание 2. Формулу интегрирования по частям удобно применять также в виде

∫ U(x) · v(x) dx   =   U(x) · V(x) − ∫ u(x) · V(x) dx,

(2)

где функция v(x) имеет очевидную первообразную V(x) , а   U(x) — дифференцируемая функция, причем ее производная   u(x) = U'(x)  является более простой функцией, чем она сама.

Замечание 3. Формулу интегрирования по частям (1) можно представить в виде в виде

∫ U(x) dV(x)   =   U(x)V(x)   −   ∫ V(x) dU(x) .

(3)

Метод интегрирования по частям применяется в следующих случаях:

1. Подынтегральное выражение содержит в качестве множителя одну из функций ln x ,   arcsin x ,   arccos x ,   arctg x . Если применить формулу (2), полагая в ней U(x) равной одной из этих функций, то подынтегральное выражение Vxu(x) может оказаться проще исходного.

2. Подынтегральное выражение имеет вид:   Pn(x) eαx ,    Pn(x)sinαx или   P(x)cosαx ,  где Pn(x) — многочлен степени n .

Интегралы от таких функций вычисляются n –кратным применения формулы интегрирования по частям (1), причем в качестве U(x) каждый раз следует брать многочлен. После каждого интегрирования по частям степень многочлена понижается на единицу.

3. Подынтегральное выражение имеет вид

eαx · cosβx,  eαx · sinβx,  sin(lnx),  cos(lnx).

После двукратного интегрирования по частям получается линейное алгебраическое уравнение относительно исходного интеграла.

4. После подведения под знак дифференциала получился интеграл   ∫ U(x) dV(x) ,   в котором функция U(x) не выражается через V(x), но функция V(x) выражается через U(x). Тогда можно применить формулу интегрирования по частям

23. Интегрирование рациональных дробей.

Если P(z) и Q(z) – многочлены в комплексной области, то - рациональная дробь. Она называетсяправильной, если степень P(z) меньше степени Q(z), и неправильной, если степень Р не меньше степени Q.

Любую неправильную дробь можно представить в виде: ,

где

P(z) = Q(z) S(z) + R(z),

 

a R(z) – многочлен, степень которого меньше степени Q(z).

Таким образом, интегрирование рациональных дробей сводится к интегрированию многочленов, то есть степенных функций, и правильных дробей, так как является правильной дробью.

 

Определение 5. Простейшими (или элементарными) дробями называются дроби следующих видов: