
- •Глава 6. Производные и дифференциалы
- •§ 6.1. Производная и её основные свойства
- •6.1.1. Дифференцируемость функции
- •6.1.2.Производная
- •6.1.3. Касательная к графику функции
- •§ 6.2. Вычисление производных
- •6.2.2. Производные элементарных функций
- •6.2.3. Производная обратной функции
- •6.2.4. Производные обратных тригонометрических функций
- •6.2.5. Производная сложной функции
- •6.2.6. Производная функции, заданной параметрически
- •§6.3. Дифференциал
- •6.3.1.Понятие дифференциала числовой функции
- •6.3.2. Геометрический и механический смысл дифференциала
- •6.3.3. Инвариантность формы первого дифференциала
- •6.3.4.Дифференциал суммы, произведения и частного функций
- •§6.4. Производные и дифференциалы высших порядков
- •6.4.1. Последовательные производные
- •6.4.3. Линейное свойство производных высших порядков
- •6.4.5. Вторая производная функции , заданной параметрически
- •6.4.6. Дифференциалы высших порядков
- •§ 6.5. Эластичность и её свойства
6.2.6. Производная функции, заданной параметрически
Рассмотрим уравнения
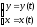 (1)
(1)
где
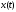 ,
,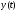 − дифференцируемые функции на некотором
промежутке
− дифференцируемые функции на некотором
промежутке ;
пусть, кроме того, функция
;
пусть, кроме того, функция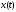 строго возрастает (или убывает) на
строго возрастает (или убывает) на и ни в одной точке этого промежутка
и ни в одной точке этого промежутка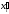 не равна 0. (Символ
не равна 0. (Символ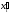 использован здесь для обозначения
производной функции
использован здесь для обозначения
производной функции по переменной
по переменной .)
.)
Тогда,
существует обратная функция
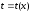 ,
причем ее производная, по теореме 6.2.2,
равна
,
причем ее производная, по теореме 6.2.2,
равна
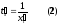
Но
тогда уравнения задают
 ,
и производная этой функции
,
и производная этой функции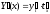 ,
по теореме6.2.3
о
производной сложной функции. Используя
равенство (2),
окончательно получаем:
,
по теореме6.2.3
о
производной сложной функции. Используя
равенство (2),
окончательно получаем:
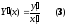
Часто вместо равенства (3) записывают равносильное ему равенство
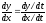
Бывает
также, что производные по параметру
 обозначают так:
обозначают так: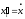 ,
,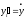 .
Тогда формула (3)
принимает вид:
.
Тогда формула (3)
принимает вид:
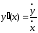 .
.
§6.3. Дифференциал
6.3.1.Понятие дифференциала числовой функции
Определение
6.3. 1.
Если числовая функция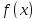 дифференцируема
в
дифференцируема
в
точке
![]() ,
то ее дифференциалом
,
то ее дифференциалом
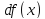 в этой точке называют
в этой точке называют
однородную
линейную функцию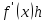 от новой независимой переменной
от новой независимой переменной .
.
Таким образом,
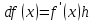 (1)
(1)
Положив
в формуле (1)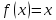 ,
получим
,
получим
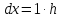 (2)
(2)
так
что дифференциал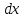 функции
функции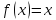 в
каждой точке
в
каждой точке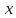 есть
есть
тождественная функция. Подставляя (2) в правую часть (1), получаем
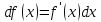 ,
(3)
,
(3)
равенство
двух линейных функций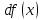 и
и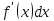 . Из него следует,
. Из него следует,
что
часто используемое обозначение
производной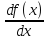 можно рассматривать,
можно рассматривать,
как
отношение дифференциалов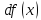 и
и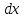 .
.
Функция
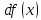 определена для всех действительных
значений
определена для всех действительных
значений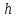 .
.
Однако
по традиции часто рассматривают
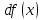 лишь на множестве тех
лишь на множестве тех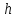 ,
,
для
которых принадлежит
области определения функции; т.е.,
принадлежит
области определения функции; т.е.,
лишь
на множестве приращений аргумента
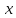 функции
функции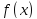 . Это объясняется
. Это объясняется
тем, что дифференциал тесно связан с приращением функции.
Так
как, по предположению,
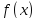 дифференцируема в точке
дифференцируема в точке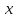 ,
то
,
то
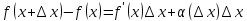 ,
(4)
,
(4)
где
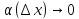 при
при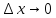 и первое слагаемое в правой части (4) –
и первое слагаемое в правой части (4) –
дифференциал,
рассматриваемый для
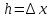 .
.
Если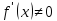 , то
, то (
(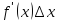 ),
),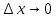 ,поэтому
говорят, что
,поэтому
говорят, что
«дифференциал есть главная линейная часть приращения функции».
6.3.2. Геометрический и механический смысл дифференциала
Пусть
числовая функция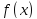 дифференцируема
в точке
дифференцируема
в точке .
Как известно,
.
Как известно,
ее
график имеет в точке
 касательную с угловым коэффициентом
касательную с угловым коэффициентом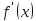 .
.
Теорема
6.3.1. Значение
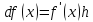 дифференциала равно
дифференциала равно
приращению
ординаты этой касательной при переходе
от
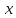 к
к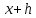 .
.
Доказательство.
Действительно,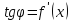 ,
,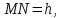 поэтому
поэтому
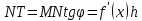 .
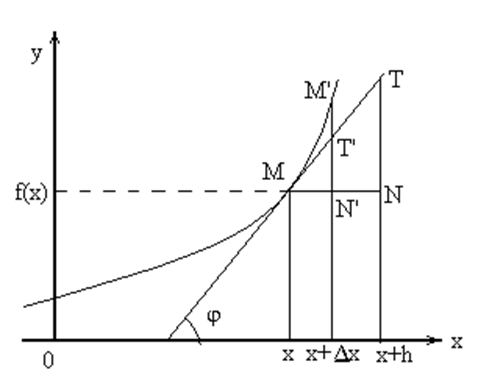
Из рисунка также видно, что
.
Из рисунка также видно, что
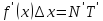
есть
часть приращения
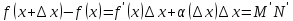 функции,
функции,
стремящаяся
к совпадению с ним при
![]() .
.
Замечание. Дифференциал допускает и механическое толкование.
Если
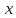 – время, а
– время, а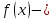 путь, пройденный прямолинейно движущейся
путь, пройденный прямолинейно движущейся
точкой
к моменту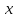 , то
, то
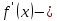 ее скорость в данный момент.
ее скорость в данный момент.
Тогда
величина
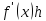 равна длине пути, который прошла бы
точка
равна длине пути, который прошла бы
точка
за
промежуток времени от
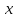 до
до
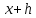 , если бы ее скорость
, если бы ее скорость
оставалась неизменной (т.е. приложенные силы уравновесились).
6.3.3. Инвариантность формы первого дифференциала
Правило дифференцирования сложной функции приведет нас к одному замечательному и важному свойству дифференциала.
Пусть
функции
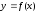 и
и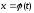 таковы, что из них может быть составлена
сложная функция:
таковы, что из них может быть составлена
сложная функция: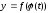 .
Если существуют производные
.
Если существуют производные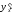 и
и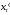 ,
то по теореме 6.2.3 существует и производная
,
то по теореме 6.2.3 существует и производная
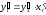 (5)
(5)
Дифференциал
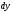 ,
если
,
если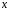 считать независимой переменной, выразится
по формуле (3). Перейдём теперь к независимой
переменной
считать независимой переменной, выразится
по формуле (3). Перейдём теперь к независимой
переменной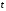 ;
в этом предположении имеем другое
выражение для дифференциала:
;
в этом предположении имеем другое
выражение для дифференциала:
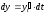 .
.
Заменяя
производную
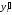 её выражением (5) и замечая, что
её выражением (5) и замечая, что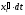 есть дифференциал
есть дифференциал как функции от
как функции от ,
окончательно получим:
,
окончательно получим:
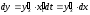 ,
,
т. е. вернёмся к прежней форме дифференциала.
Таким образом, мы видим, что
форма дифференциала может быть сохранена даже в том случае, если прежняя независимая переменная заменена новой.
Мы всегда имеем право писать
дифференциал
 как в форме (1), будет ли
как в форме (1), будет ли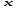 независимой переменной или нет; разница
лишь в том, что, если за независимую
переменную выбрано
независимой переменной или нет; разница
лишь в том, что, если за независимую
переменную выбрано ,
то
,
то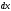 означает не произвольное приращение
означает не произвольное приращение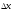 ,
а дифференциал
,
а дифференциал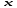 как функции от
как функции от .
Это свойство и называютинвариантностью
формы дифференциала.
.
Это свойство и называютинвариантностью
формы дифференциала.
