§15.5. Свойства определённого интеграла

Распространим определение интеграла на случай .

Определение. Если , то по определению,

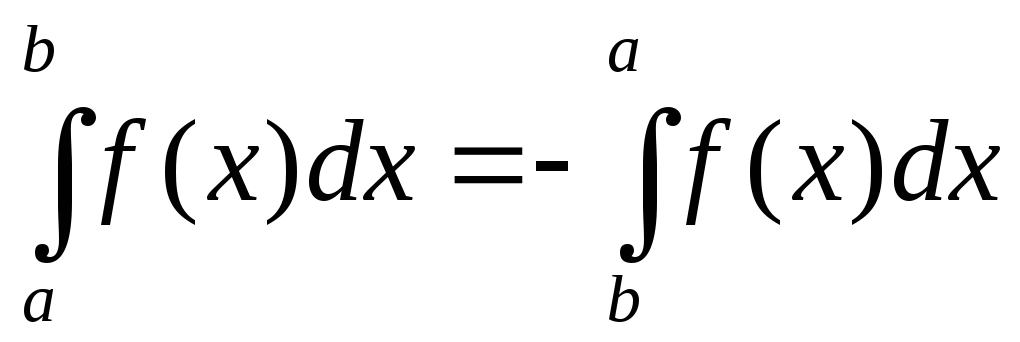, (14) если интегрируема на отрезке.

Также по определению положим 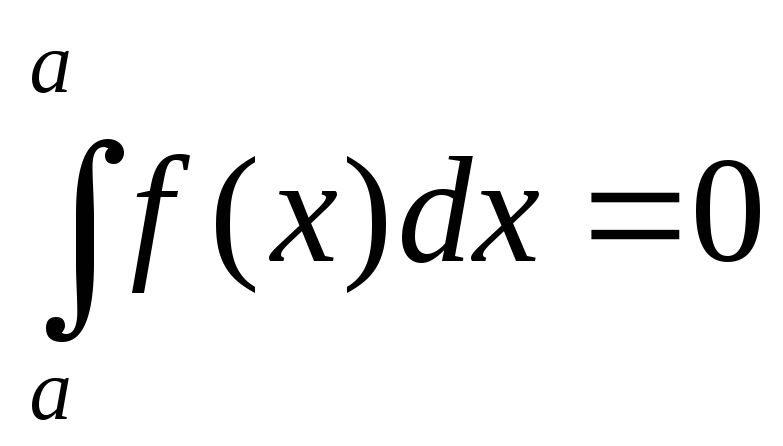(15) Заметим, что равенство (14) справедливо и в случае, так как тогда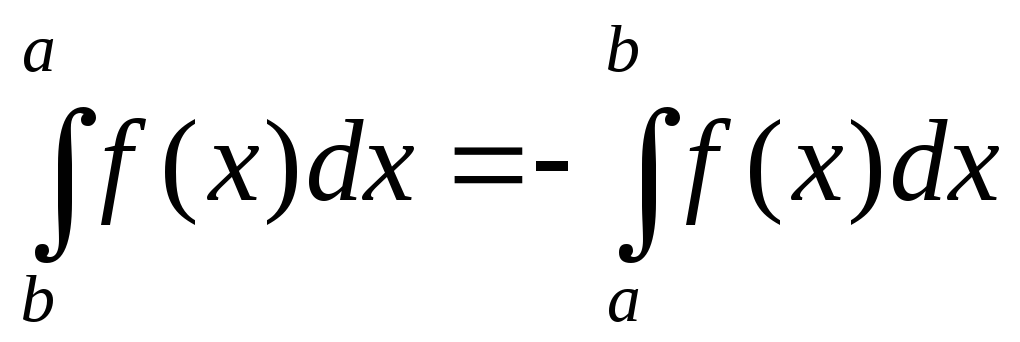, что равносильно равенству (14).

Это замечание, вместе с определением (15), означает, что равенство (14) выполняется при всех и.

Теорема 15.10. Пусть функция интегрируема на отрезке,. Тогдаинтегрируема на любом .

►Рассмотрим произвольное разбиение отрезка и проведем разбиение оставшихся частей отрезка.

В итоге будет получено разбиение отрезка, причем точкиивойдут в число точек деления этого разбиения.

Рассмотрим сумму , соответствующую разбиениюотрезкаи выделим часть это суммы, соответствующую тем отрезкам разбиения, которые входят в.

Так как ,, а суммаявляется частью суммы, очевидно неравенство.

Поскольку за счет выбора диаметра разбиения величину можно сделать меньшей любого заданного, то же верно и для, что означает интегрируемостьна.◄

Теорема 15.11. Пусть интегрируема на отрезкахи. Тогда она интегрируема и на отрезке, причем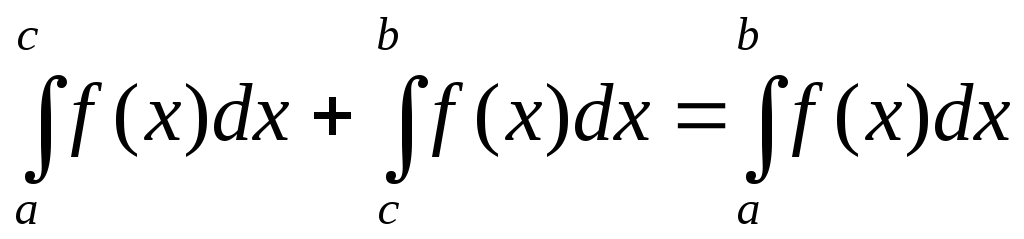 (16)

► По условию, для любого существует такое, что для разбиения отрезковис диаметром меньшим, выполняются неравенства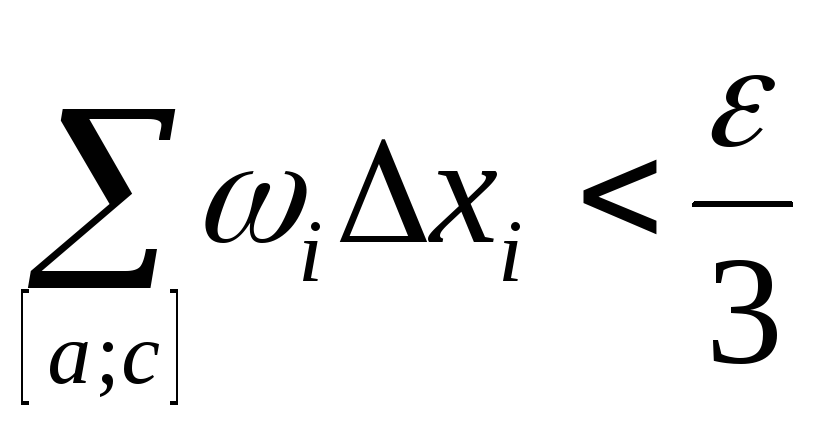,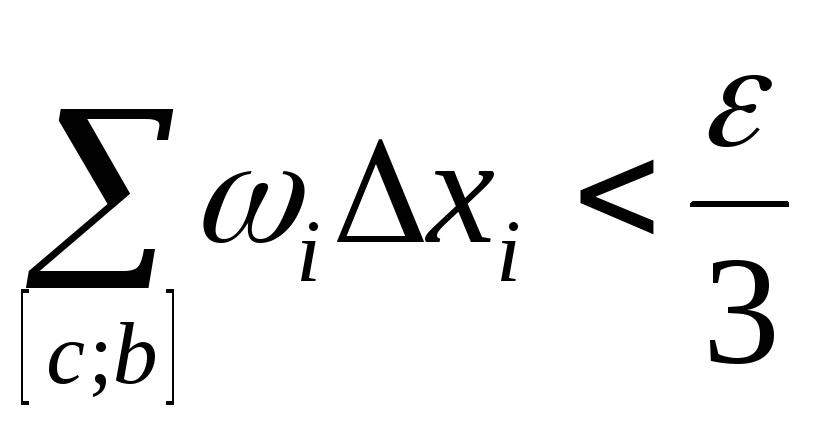. Рассмотрим теперь произвольное разбиениеотрезка. Если точкапопала в число точек деления, то сумма

Если же не попала в число точек деления, то при некотором,,. Тогда(17)

Обе суммы стоящие в правой части (17), не превосходят, соответственно, и.

Так как функция ограничена наиона ограничена и на всем отрезке. Пустьисоответственно, точная нижняя и точная

верхняя грани множества её значений. Поэтому .

Следовательно, при достаточно малом d(T) все три величины ,именьше, чем, а с ними и величина

Таким образом, интегрируема на _.

Чтобы доказать формулу (16), обозначим

, ,,

и рассмотрим произвольное число . Согласно определению интеграла Римана, существует такое число, что

(18)

для всех размеченных разбиений отрезкас диаметром; существует такое число, что

(19)

для всех размеченных разбиений отрезкас диаметроми существует такое число, что

(20)

для всех размеченных разбиений отрезкас диаметром. Положим,, и рассмотрим такое размеченное разбиениеотрезкаси такое размеченное разбиениеотрезкас, для которых точкане входит в наборы и.

Тогда объединение разбиений иобразует некоторое размеченное разбиениеотрезкас, для которого справедлива формула. Поэтому, с учетом неравенств (18)(20), имеем оценки

(21)

.

В силу произвольного выбора числа , число, стоящее в левой части (21), равно нулю; т.е.,, что равносильно формуле (16). ◄

Равенство (16) выражает свойство аддитивности интеграла по отрезку. Заметим, что это свойство, ввиду (14) останется верным при любом взаимном расположении точек .

Теорема 15.12. Если интегрируема на , то для любого числа функция интегрируема на и .

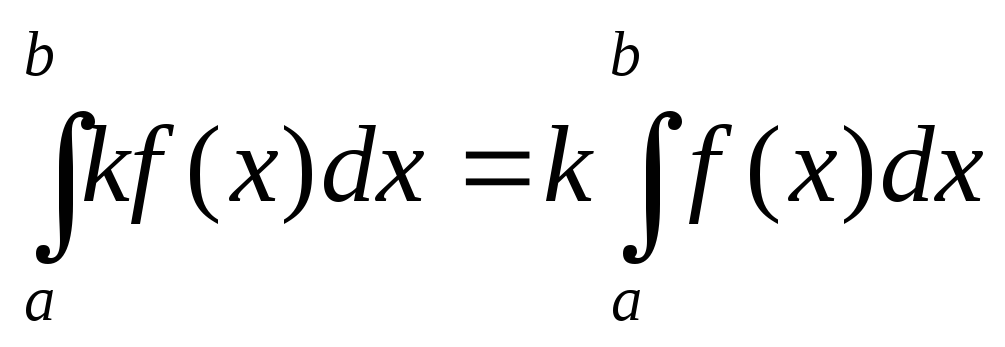►Обозначим суммы Дарбу для . Посколькунеравенство

выполняется при ввиду интегрируемости.Доказываемое равенство интегралов вытекает при стремлениик 0 из очевидного равенства интегральных сумм

_.◄

Теорема 15.13. Если - интегрируемы на , то и - интегрируема на и

► Докажем теорему сначала для суммы функций. Обозначим суммы Дарбу дляи.

Далее, ,.

Поэтому, при ,имеем:

.

Итак, интегрируемость доказана. Равенство интегралов следует теперь из равенства для интегральных сумм при стремлении к 0. Для доказательства теоремы для разности функций достаточно рассмотреть функциии.◄

Теорема 15.14. Если на ,и интегрируема на , то

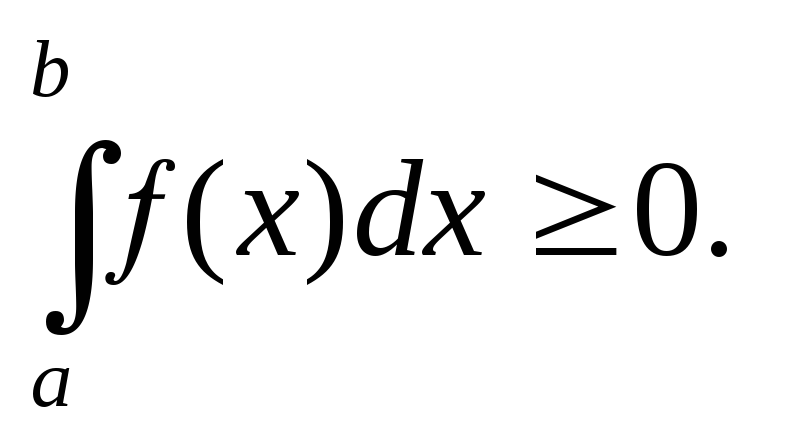
► По условию, длю любого разбиения и любого выбора точек выполняется неравенство. Поэтому и, т. к., .◄

Теорема 15.15. Если - интегрируемы на и для всех имеет место неравенство , то

(22)

► По теореме 15.13 функцияинтегрируема. По теореме 15.14, 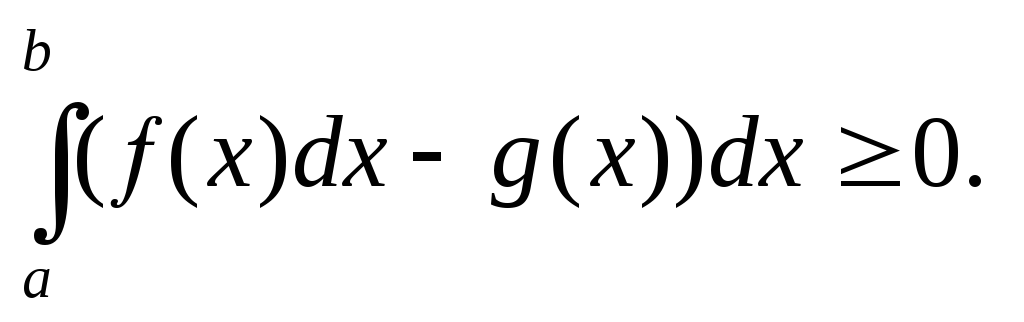(23)

Вновь по теореме 15.13,

Поэтому из (23) следует (22).◄

Теорема 15.16. Пусть интегрируема на . Тогда интегрируема на и

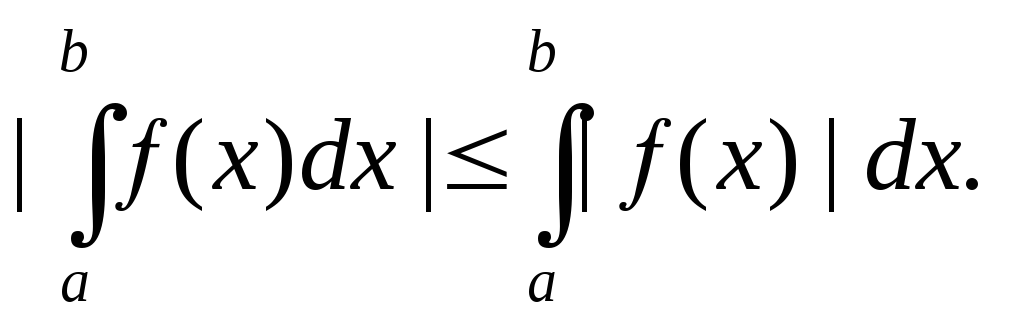(24)

►Известно, что для всех выполнено неравенство. Значит, для любых

.

Из этого следует, что колебание функциина отрезкене превосходит колебания функции на . Значит,

при достаточно малом . Это доказывает интегрируемость функции .

Наконец,

(25)

(т. к.для любых чисел ).

Из (25) при следует (24).◄