Резниченко а.Н.(гр. 512)

Отчёт

Изучение законов колебательного движения математического маятника.

Цель работы: исследовать колебания математического маятника, по измерениям его периода определить ускорение свободного падения.

Оборудование: установка для изучения свойств математического маятника, линейка.

Математический маятник

Математическим маятником называют тело, которое может качаться вокруг неподвижной точки, причем практически вся масса тела сосредоточена в одной точке.

Хорошим примером такого маятника является металлический шарик, подвешенный на тонкой длинной нити.

Если растяжением нити можно пренебречь, то длина маятника (l) остается постоянной при движении. Траекторией движения материальной точки является, таким образом, дуга окружности, радиус которой равен l. Для описания движения в этом случае удобно воспользоваться естественным способом определения положения точки.

Его можно определить дуговой координатой L, отсчитываемой вдоль траектории от некоторого начала О. Поместим начало отсчета в точку, соответствующую положению равновесия, и примем, что смещение маятника вправо от точки О характеризуется положительной координатой, а влево – отрицательной. Уравнение движения (второй закон Ньютона), если пренебречь силами сопротивления, имеет вид:

где m – масса, L – дуговая координата, l – длина маятника,  – угол отклонения маятника от положения равновесия.

Воспользовавшись известным соотношением:

перепишем соотношение (1a):

При рассмотрении малых колебаний можно принять:

тогда (1a) примет следующий, вид:

Обозначим далее:

где ₀ – круговая (циклическая) частота является постоянной величиной для данного маятника. Уравнение (3) можно теперь привести к конечному виду:

Получено очень важное в физике уравнение. Такое уравнение можно получать для различных систем и не обязательно механических: для каждой из них по-своему запишется левая часть уравнения (4) (но ее размерность всегда будет 1/c). Cистема, поведение которой описывается уравнением (5), называется гармоническим осциллятором.

Решение уравнения (5) имеет вид:

В том, что (6) является решением (5), можно убедиться, подставив (6) в (5). Уравнение (6) описывает колебательный процесс около некоторого равновесного состояния. Входящие в него константы характеризуют максимальное отклонение от равновесного положения - амплитуду колебания А₀ и состояние системы в начальный момент - начальную фазу колебания ₀.

Время одного колебания (Т) называется периодом:

Запишем теперь уравнение движения математического маятника с учетом сил сопротивления:

Силой сопротивления в данном случае является трение о воздух. При небольших скоростях движения для нее можно воспользоваться известным законом:

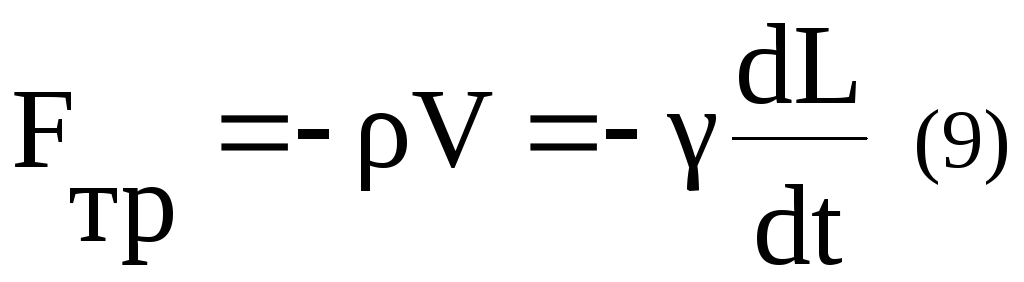
где  – коэффициент пропорциональности, V – скорость тела относительно воздуха.

Если ограничиться рассмотрением малых колебаний, то (8) можно переписать так:

где, кроме уже известных, принято следующее обозначение:

Уравнение (10) описывает также поведение различных систем в случаях, когда нельзя пренебречь силами сопротивления, которые определяются выражением, подобным (9). Если (5) описывало систему, совершающую бесконечно длящиеся (незатухающие) колебания, то (10) описывает затухающие колебания. Они со временем уменьшаются до полного прекращения.

Решение (10) имеет вид:

При подстановке (11) в (10) получим тождество, если примем:

Таким образом, циклическая частота затухающих колебаний несколько меньше ₀, а их амплитуда уменьшается со временем:

Для характеристики системы, совершающей затухающие колебания, используются следующие величины:

• время релаксации , в течение которого, амплитуда колебания A(t) уменьшается в е раз (е – основание натурального логарифма)

• логарифмический декремент затухания d характеризует убывание амплитуды за один период колебания:

добротность системы, характеризующая рассеяние энергии при колебании:

Из определения времени релаксации следует:

то есть:

Можно определить число колебаний, совершенных системой за время :

Далее можно записать следующие равенства: