QUADMET

УДК 518.5 Квадратурные формулы. Численное интегрированиею /сос. В.В.Кулинич - Нижний Новгород, изд. ННГУ им.Н.И.Лобачевского, 2005 г. -24 с.

Излагаются основные методы построения алгоритмов для численного нахождения интегралов Римана. Приводится полный текст адаптивной программы с описанием на алгоритмическом языке Фортран для нахождения интеграла Римана методом, основанном на формуле Ньютона-Котеса 8-го порядка. Формулируются задания для самостоятельной работы по вычислительному практикуму.

Методическая разработка рассчитана на студентов Нижегородского госуниверситета.

Составители:

Виктор Валентинович Кулинич

Нижегородский государственный университет им.Н.И.Лобачевского 2003 г.

Задача вычисления интеграла Римана является одной из старейших задач теория численных методов и состоит в замене вычисления

Z ¯

®

алгоритмом из конечного числа операций. Для построения алгоритмов вычисления интеграла (1) воспользуемся стандартной схемой для решения различных задач в функциональных пространствах. Стандартная схема содержит несколько шагов, включающих в себя дискретизацию функциональных пространств конечномерными пространствами, аппроксимацию операторов, действующих в функциональных пространствах, конечномерными и установлении условий сходимости приближенных решений к исходным решениям.

1. Дискретизация пространства. Пусть функция f(x) принадлежит метрическому пространству H[®;¯]. Для построения численного алгоритма пространство H[®;¯] дискретизируем последовательностью конечномерных пространств Rn; n ! 1 . Связь между пространствами H[®;¯] и пространством Rn зададим посредством последовательности линейных операторов Tk; ; k = 1; 2; : : : ; n; причем предположим, что

Операторы Tn будем называть операторами проектирования. Элементы fn пространств Rn будем использовать для аппроксимации элементов f пространства H[®;¯]. Близость элементов fn 2 Rn к элементам H[®;¯], будем оценивать с помощью числа

½(fn; Tnf) = jjfn ¡ TnfjjRn:

Определение 1. Будем говорить, что ппоследовательность ffng1n=1 Tn -сходится к элементу и писать

Tn

fn ! f:

3

Заметим, что Tn-предел может быть не единственным. Проиллюстрируем введенные понятия примером. Пусть f 2 C[m®;¯] пространство н непрерывных с m-производной на отрезке [®; ¯] функций. Дня построения оператора проектирования на отрезке [®; ¯] рассмотрим множество !n = (x(in) : ® · x(1n) < x(2n) < : : : < x(nn) · ¯) которое будем называть сеткой отрезка [®; ¯]. Точки x(In) будем называть узлами сетки . Оператор проектирования Tn ставящий в соответствие каждой функции f 2 C[m®;¯] столбец ее значений в узлах сетки !n зададим формулой

Tn- сходимость последовательности ffig1i=1 = ff(x(in))g1i=1 к функции

Иными словами норма в Rn для функции f 2 C[m®;¯] согласована с нормой что и обеспечивает единственность Tn - предела. Условие hn ! 0

при n ! 1 обеспечивает "хорошее приближение"отрезка сеткой !n.

2. Аппроксимация. Интеграл (1) можно рассматривать как оператор

Z ¯

A[f] = f(x)dx;

®

имеющий областью определения пространство H[®;¯], а областью значений пространство R1.

Пользуясь общей схемой, оператор A аппроксимируем последовательностью конечномерных операторов An, имеющих областью определения пространство Rn, а областью значений пространство R1 .

Определение 2. Будем говорить, что на элементе f 2 H[®;¯] выполнено условие аппроксимации (или последовательность fAng1n=1 аппроксимирует

оператор A на элементе f, если

Z ¯

jjAn[fn] ¡ A[f]jj = jjAn[fn] ¡ jj ! 0; n ! 1:

®

4

Оператор A в теории численного интегрирования обычно задается формулой

В теории формулу ( 4), задающую аппроксимирующий оператор An, на-

зывают квадратурной формулой, определяемой весовыми коэффициентами Ci(n) и узлами x(in) сетки !n. Элемент fn = ff(x(1n); : : : ; f(x(nn)g пространства Rn называют сеточной функцией, заданной на сетке !n. Величину

®i=1

называют функционалом погрешности квадратурной формулы. К сожалению даже в случае H[®;¯] = C[®;¯] имеет место

Теорема 1. Для любой системы узлов и весовых коэффициентов функционал погрешности ±n[f] не стремится сильно к нулю на множестве C[®;¯],

более того, всегда

jj±n[f]jj = ¯ ¡ ® + Xn jCi(n)j:

i=1

Из приведенной теоремы следует, что проблема численного интегрирования на C[®;¯] , неразрешима. Однако, для практических приложений важен другой результат, состоящий в том, что существует система узлов и

n!1

весовых коэффициентов таких, что ±n[f] ! 0 слабо на C[®;¯].

Более того, в приложениях, как правило, имеют дело с некоторым компактом (множество где может быть выделена фундаментальная последовательность ) X 2 C[a;b] и тогда для f 2 X можно указать даже порядок стремления к нулю функционала погрешности. Из слабой сходимости следует, вообще говоря факт, что для каждой функции следует строить свою квадратурную формулу.

Определение 3. Пусть дана после последовательность функционалов ffn(x)g; x 2 X. Будем говорить, что последовательность сильно сходится к функционалу f(x); x 2 X, если

jjfn(x) ¡ f(x)jj = sup jfn(x) ¡ f(x)j ! 0; n ! 1:

jjxjj·1

Определение 4. Пусть дана последовательность функционалов fn(x); x 2 X. Будем говорить, что последовательность слабо сходится к функционалу

5

f(x); x 2 X, если

fn(x) ! f(x); n ! 1

для любого x 2 X. Имеют место теоремы:

Терема 2. Для того, чтобы ппоследовательность функционалов погрешностей в

±nf ! 0

n!1

слабо для любой непрерывной функции, необходимо и достаточно, чтобы

Xn jCi(n)j · K для любого n,

i=1

где K- постоянная.

Теорема 3. Если вcе весовые коэффициенты квадратурной формулы положительны, тогда последовательность функционалов погрешности

±nf ! 0;

n!1

слабо для любой непрерывной функции множества C[®;¯].

3. Квадратурные формулы интерполяционного типа. Многообразие квадратурных формул вида (4) определяемся требованиями, предъявляемыми к алгоритмам вычисления интеграла (1) и классом функций к которым применяется данный алгоритм.

Общая проблема построения квадратурных формул заключается в следующем. Пусть задано пространство H[®;¯] и натуральное число n, Требуется среди всех квадратурных формул вида

являлась наименьшей.

Таким образом, речь идет о таком выборе на отрезке [®; ¯] узлов сетки xi 2 !n и весовых коэффициентов Ci(n), при котором приближенное значение интеграла, даваемое квадратурной формулой, было наилучшим.

Можно видоизменить поставленную задачу, если искать в указанном смысле квадратурную формулу, в которой либо узлы, либо весовые коэффициента подчинены заранее определенным требованиям. Наиболее просто

6

поставленная задача решается для заранее определенной системы узлов и заранее определенного класса интегрируемых функций.

Предположим, что интегрируемая функция принадлежит классу C[®;¯] и задана сетка !n отрезка [®; ¯]. Для получения весовых коэффициентов квадратурных формул используем следующую процедуру. Рассмотрим задачу, обратную к задаче дискретизации, т.е. задачу восстановления элемента f 2 H[®;¯] по заданной сеточной функции fn 2 Rn. Из общей теории известно, что данная задача имеет не единственное решение и наиболее просто решается при помощи интерполяционных многочленов, если имеется априорная информация о гладкости искомых функции.

Так в случае H[®;¯] выбирая в качестве интерполяционного многочлена интерполяционный многочлен Лагранжа, будем иметь

Подставляя (6) в (1), будем иметь

Первое слагаемое в правой ччасти равенства (8) называют кквадратурной формулой Ньютона-Котеса, второе - остаточным членом. Приведем ряд формул НьютонаКотеса для малых n.

3.1. Квадратурная формула трапеций (n = 1) :

7

3.3. Квадратурная формула 3/8 (n = 3) :

3.4. Квадратурная формула Буля (n = 4) :

Заметим, что при n > 10 среди весовых коэффициентов квадратурных формул НьютонаКотеса всегда будут появлятся отрицательные, причем имеет место соотношение

Из соотношения (15) вытекает теорема.

Теорема 4. Существуют непрерывные функции для которых процедура численного интегрирования, основанная на формулах Ныотона-Котеса неограниченно расходится.

В силу построения, квадратурные формулы Ньютона-Котеса точны для многочленов степени n. Для весовых коэффициентов имеет место

Теорема 5. Если узлы x(in) сетки !n расположены симметрично относительно середины отрезка [®; ¯], тогда весовые коэффициенты, квадратурной формулы, соответствующие симметричным узлам равны между, собой.

Такие "симметричные"квадратурные формулы обладают дополнительным свойством, которое формально не предусмотрено их построением. Они являются точными для любой функции, нечетной относительно середины

8

отрезка [®; ¯] и являются точными для многочленов степени n + 1 при n четном. Для получения оценки остаточного члена в этом случае, достаточно середину отрезка [®; ¯] считать кратным узлом и в формуле остаточного члена n заменить на n + 1 .

Приведем оценки остаточного члена квадратурных формул НьютонаКотеса для малых n.

3.9. Квадратурные формулы Гаусса:

Исключая условие фиксированности сетки !n при построении квадратурной формулы, Гауссом показано, что максимальный алгебраический порядок точности квадратурной формулы будет n+1 для сетки !n с n узлами, если в качестве интерполяционного многочлена при построении квадратурной формулы будет взят многочлен

При атом узлами сетки !n отрезка [¡1; 1] будут являться нули многочлена Лежандра Pn+1(x):

Весовые коэффициенты при этом н находятся по формуле

9

и обладают свойством положительности для всех n. Остаточный член квадратурной формулы можно оценить по выражению

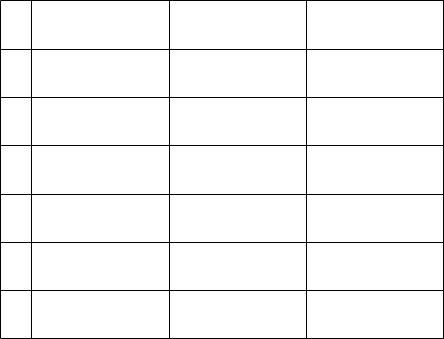
В таблице I приведены для различных n узлы сетки !n и весовые коэффициенты. Вследствие симметрии узлов относительно середины отрезка [¡1; 1] указаны лишь неотрицательные узлы и весовые коэффициента при них.

Таблица 1.

10:0000000000

2:0000000000

20:5773502692

1:0000000000

30:0000000000 0:7745966692

0:8888888888 0:555555556

40:8611363115 0:3399810436

0:347854851 0:6521451549

50:0000000000 0:9061798459 0:5384693101

0:5688888888 0:4786286705 0:2369268851

60:9324695142 0:6612093864 0:2386191861

0:1713244924 0:3607615730 0:4679139346

3.10. Квадратурная формулы Филона:

В приложениях интегрируемая функция в интеграле (1 ) часто представима в виде

где

º(¯ ¡ ®) >> 1; ' 2 C[n®;¯]:

Тогда представляется более выгодным при построении квадратурной формулы дискретизировать пространство функций ', так как дискретизация пространства функций f(x) потребует квадратур, точных для многочленов степени больше, чем º(¯ ¡ ®)=¼:

Выполняя дискретизацию пространства C[n®;¯] функции '(x) и восста-

навливая функцию '(x) с помощью интерполяционного многочлена Лагранжа, для вычисления интеграла (1) получим квадратурную формулу

10