§2. Комбинаторика без повторений.

Для построения соответствующих математических моделей комбинаторных задач будем использовать математический аппарат теории множеств. Может случиться, что в данном множестве порядок следования элементов не важен, а важен только состав множества. Но есть задачи, в которых прядок элементов является существенным.

Определение 1: Порядок во множестве изэлементов – это нумерация его элементов натуральными числами, т.е. отображение множествана множество.

Определение 2: Множество с заданным на нем порядком называется упорядоченным множеством.

Очевидно, что множество, содержащее более одного элемента, можно упорядочить не единственным способом.

Например, из двух букв иможно построить упорядоченное множество двумя различными способами:

и .

Три буквы ,иможно расположить в виде последовательности шестью способами:

, ,,,,.

Для четырех букв путем перебора получим уже 24 различных упорядоченных последовательностей.

Упорядоченные последовательности элементов некоторого множества можно рассматривать как распределения или расстановки этих элементов в последовательности.

Определение 3: Пусть дано конечное множество изэлементов. Всякий набор изэлементов данного множества (при этом элементы в наборе могут и повторяться) будем называть-расстановками.

Через понятие расстановки вводятся основные определения комбинаторики: сочетания, размещения и перестановки. При этом каждое из этих понятий может быть с повторениями и без повторений. В данном параграфе будут рассмотрены комбинаторные формулы без повторений.

Перестановки без повторений.

Определение 4: Пусть - конечное множество изэлементов.Перестановками из различных элементов множестваназываются все расположенияэлементов в определенном порядке. Обозначается:(от французского словаpermutation - перестановка).

Упорядоченные множества считаются различными, если они отличаются либо своими элементами, либо их порядком.

Определение 5: Различные упорядоченные множества, которые отличаются лишь порядком элементов, называются перестановками этого множества.

Последнее определение сформулировано с позиции теории множеств.

Определение 6: Произведение последовательных натуральных чисел в математике обозначаюти называютфакториалом.

Выбор для обозначения восклицательного знака, возможно, связан с тем, что даже для сравнительно небольших значенийчислоочень велико. Например,,,,,,,и т.д.

Теорема 1: Число перестановок из различных элементов вычисляется по формуле:

(1)

Доказательство. Рассмотрим произвольное множество из элементов. Построим всевозможные расстановки из этихэлементов. На первое место расстановки можно поставить любой из элементов (способов выбора первого элемента). После того, как первый элемент выбран и независимо как он выбран, второй элемент можно выбратьспособом. Для выбора третьего элемента остаетсяспособа и т.д. Последний элемент выбирается соответственно одним способом. Тогда, в силу комбинаторного принципа умножения, количество таких расстановок будет равно:

Теорема доказана.

Пример 1: Сколькими способами трое друзей могут занять в кинотеатре места с номерами 1, 2 и 3.

Решение. Количество искомых способов будет равно числу перестановок без повторений из трех элементов: способов. При необходимости эти способы можно перебрать.

Перестановки букв некоторого слова называют анаграммами. Открытые еще в ІІІ веке до нашей эры греческим грамматиком Ликофроном анаграммы до сих пор привлекают внимание языковедов, поэтов и любителей словесности. Мастера словесных игр помимо эрудиции и большого запаса слов знают много секретов, связанных с комбинаторными навыками, один из которых – анаграммы. Часто требуется среди всех перестановок выбрать те, которые обладают определенным свойством. Например, среди анаграмм слова «крот», которых всего , только одна, не считая самого слова«крот», имеет смысл в русском языке – «корт».

Кроме линейных перестановок, можно рассматривать перестановки круговые (или циклические). В этом случае перестановки, переходящие друг в друга при вращении, считаются одинаковыми и не должны засчитываться.

Теорема 2: Число круговых перестановок из различных элементов равно

Пример 2: Сколькими способами 7 детей могут стать в хоровод?

Решение. Число линейных перестановок 7 детей будет равно . Если хоровод уже сформирован, тогда для него существует 7 круговых перестановок, переходящих друг в друга при повороте. Эти перестановки не должны быть засчитаны, поэтому круговых перестановок из 7 элементов будет.

Размещения без повторений.

Определение 7: Пусть имеется различных предметов. Расстановки изэлементов поэлементов () называютсяразмещениями без повторений. Обозначают: . Здесь имеется в виду, что элементы в расстановках не повторяются.

В данном определении существенной является следующая позиция: две расстановки различны, если они отличаются хотя бы одним элементом или порядком элементов.

Приведем еще одно определение размещений, эквивалентное исходному, более простое для понимания.

Определение 8: Конечные упорядоченные множества называются размещениями.

Теорема 3: Количество всех размещений из элементов поэлементов без повторений вычисляется по формуле:

. (2)

Доказательство. Пусть имеется произвольное множество , состоящее изэлементов. Необходимо выбрать из этого множестваразличных элементов. Причем, важен порядок выбора.

Выбор элементов осуществляется поэтапно. Первый элемент расстановки можно выбрать различными способами. Тогда из оставшихся элементов множествавторой элемент расстановки выбираетсяспособом. Для выбора третьего элемента возможноспособа и т.д. Тогда для выбора- го элемента имеемспособ. Следовательно, согласно правилу умножения, количество таких расстановок будет равно:

.

По определению, такие расстановки являются размещениями. Что и требовалось доказать.

Пример 3: Собрание из 25 человек выбирает президиум из 3 человек: 1) председатель, 2) заместитель, 3) секретарь. Сколько возможно вариантов выбора президиума?

Решение. Выбирая трех человек из 25, замечаем, что важен порядок выбора, поэтому количество президиумов будет равно:

.

Замечание: Число размещений без повторений можно также находить по формуле:

. (3)

Если в знаменателе дроби из формулы (3) , то принято считать.

Замечание: Формула (3) отличается компактностью, но при решении задач удобнее использовать формулу (2). Дробь, стоящая в правой части формулы (3), может быть сокращена до целого числа. Это число равно числу из правой части формулы (2).

Пример 4: Сколько можно составить двухбуквенных слов (буквы не повторяются) из 33 букв русского алфавита?

Решение. В данном случае мы имеем дело не со словами в лингвистическом понимании, а с буквенными комбинациями произвольного состава.

Тогда количество различных комбинаций из 2 букв, выбранных из 33 букв алфавита, будет равно:

.

В данном случае важен порядок букв. Если поменять 2 буквы в слове, то получим новое слово.

Замечание: Перестановка без повторений – это частный случай размещений без повторений при . Можно сказать, что перестановка изэлементов – это размещение изэлементов поэлементов:

В некоторых задачах по комбинаторике не имеет значения порядок расположения объектов в той или иной совокупности. Важно лишь то, какие именно элементы ее составляют. В таких ситуациях мы имеем дело с сочетаниями.

Сочетания без повторений.

Определение 9: Сочетания без повторений из элементов некоторого множества поэлементов () – это расстановки, отличающиеся друг от другасоставом, но не порядком элементов. Обозначают: (от французского словаcombinaison – сочетание).

В данном случае в расстановках важен состав, а не порядок элементов в подмножестве. Если две расстановки отличаются только порядком следования элементов, то с точки зрения сочетаний они не различимы. Элементы в этих расстановках не повторяются.

С точки зрения теории множеств определение сочетаний можно сформулировать иначе.

Определение 10: Конечные неупорядоченные множества называются сочетаниями.

Таким образом, сочетания – это такая выборка элементов, при которой их порядок совершенно не важен.

Сочетаний из элементов поэлементов должно быть меньше, чем соответствующих размещений. Это следует из того, что не надо засчитывать расстановки одинакового состава.

Теорема 4: Число сочетаний находится по следующей формуле:

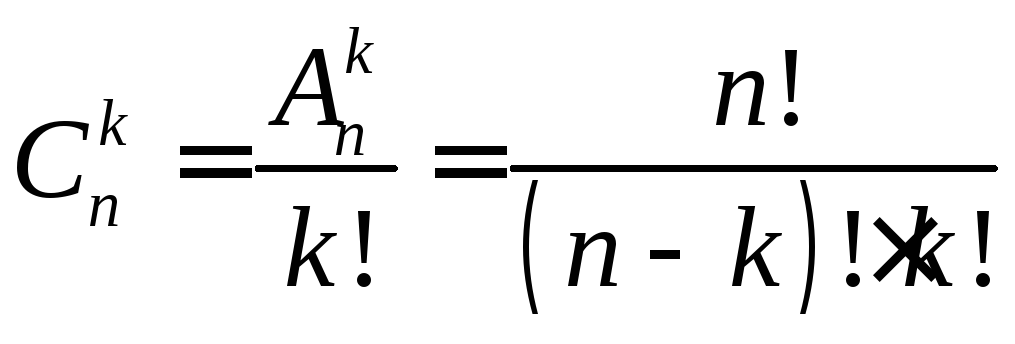. (4)

Доказательство. Если из произвольного -элементного множества выбраныэлементов, то их можно пронумеровать номерамичислом способов, равным. Оставшиесяэлементов можно занумеровать номерами,, …,всегоспособами. Кроме того, сам отборэлементов изэлементов можно осуществитьспособами. Таким образом, мы получили вариантов нумерации полного множества из элементов, которых всего. Поэтому имеем, откуда получаем:

.

Теорема доказана.

Замечание: Дробь, стоящая в правой части (4), может быть сокращена до целого числа.

Из формулы числа сочетаний следует:

, ,.

Формула (4) может быть преобразована к виду: . Отсюда видно, что число размещенийвраз больше числа соответствующих сочетаний. Другими словами, чтобы посчитать все сочетания, нужно исключить из всех размещенийподмножества, отличающиеся порядком (их будетштук), т.е.делят на.

Пример 5: Сколькими способами можно выбрать 3 различные краски из имеющихся пяти.

Решение. Порядок выбора красок не важен. Важно только какие краски выбраны. Поэтому количество вариантов равно: .

Пример 6: Сколькими способами можно пошить трехцветные полосатые флаги, если имеется материал пяти различных цветов.

Решение. Порядок выбора полос важен, поэтому количество таких флагов равно: .