3.3. Вероятность появления хотя бы одного события

В жизни, производстве часто возникают такие ситуации, когда нужно вычислить вероятность появления хотя бы одного события из некоторого набора возможных событий. Например, если по цели был сделан залп из нескольких орудий, то интерес представляет вероятность того, что цель будет поражена, т.е. что будет хотя бы одно попадание.

Математически такую схему событий можно представить следующим образом. Пусть имеется n независимых событий A₁, A₂, ..., A_n, причем известны вероятности каждого из этих событий. Пусть A – появление хотя бы одно из этих событий, тогда противоположное событие  означает, что ни одно из этих событий не появится. Поскольку P(A)=1–P()=1–P(₁₂..._n)=1–P(₁)P(₂)...P(_n), то вероятность появления хотя бы одного из событий A₁,A₂,...,A_n равна

P(A₁+A₂+...+A_n) = 1– P(₁)P(₂)...P(_n). (3.9)

Если события A_i равновероятны, то можно положить P(₁)=P(₂)= ... =P(_n)=q. Тогда формула (9) примет следующий вид:

P(A₁+A₂+...+A_n) = 1– qⁿ (3.10)

Пример 3.8. Вероятности попадания в цель при стрельбе из трех орудий таковы: p₁=0,8, p₂=0,7, p₃=0,9. Найти вероятность хотя бы одного попадания при одном залпе из всех орудий.

Решение. Поскольку вероятности попаданий независимы и q₁=1–p₁=0,2, q₂=1–p₂=0,3, q₃=1–p₃=0,1, то искомая вероятность равна

P(A) = 1–q₁q₂q₃ = 1–0,006 = 0,994.

Пример 3.9. Вероятность того, что при одном выстреле стрелок попадет в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?

Решение. Вероятность попадания хотя бы один раз при n выстрелах равна:

P(A) = 1–qⁿ.

Поскольку P(A)0,9 и q=1–p=0,6, то

1–0,6ⁿ  0,9  0,6ⁿ  0,1  nlg0,6  lg0,1 

 .

Таким образом, чтобы хотя бы один раз попасть в цель с вероятностью не менее 0,9 стрелок должен произвести не менее 5 выстрелов.

3.4. Формула полной вероятности

На практике часто возникают ситуации, когда требуется определить вероятность события, которое может произойти только с одним из событий, образующих полную группу. Например, требуется проверить качество деталей, расположенных по нескольким ящикам; оценить надежность прибора, который может работать в нескольких режимах, и т.д.

Теорема. Если событие А может осуществляться только при выполнении одного из событий В₁, В₂, ... , B_n, которые образуют полную группу несовместных событий, то P(A) вычисляется по формуле:

, (3.11)

которая называется формулой полной вероятности.

Доказательство. Согласно условию теоремы, событие А может наступить, если появится одно из событий B₁, B₂, ... , B_n. Это означает, что появление события А влечет появление одного из следующих событий: B₁A, B₂A, ... , B_nA, неважно какого. По этому событие А можно представить в виде A= B₁A+B₂A+...+B_nA. Так как события B₁, B₂, ... , B_n несовместны, то, очевидно, что несовместны и события B₁A, B₂A, ... , B_nA. Тогда применяя теорему сложения вероятностей несовместных событий, получим

P(A) = P(B₁A)+P(B₂A)+...P(B_nA).

Далее, в соответствии с теоремой умножения вероятностей, получим формулу полной вероятности (11).

Пример 3.10. Партия деталей изготовлена двумя рабочими. Первый изготовил 2/3 деталей партии, второй – 1/3. Вероятность брака для первого рабочего равна 1%, для второго – 10%. На контроль взяли одну деталь. Какова вероятность того, что она бракованная?

Решение. Пусть А – событие, состоящее в том, что взятая наудачу деталь бракованная. Здесь возможны два случая: 1) деталь изготовлена первым рабочим (событие В₁), 2) деталь изготовлена вторым рабочим (событие В₂). Очевидно, что события В₁ и В₂ несовместны и образуют полную группу. Их вероятности, по условию, равны

и .

Условные вероятности события А равны

и .

Следовательно, по формуле полной вероятности, находим вероятность того, взятая деталь будет бракованной:

.

Пример 3.11. В первой урне находится 5 белых и 3 черных шара. Во второй – 4 белых и 5 черных шара. Из первой урны во вторую наугад перекладывают два шара. После этого из второй урны вынимают сразу 4 шара. Какова вероятность того, что шары будут одного цвета?

Решение. результат второго испытания (т.е. вынимание шаров из второй урны) зависит от того, какие шары были переложены из первой урны. Здесь возможны три случая:

B₁ = {оба шара белые},

B₂ = {оба шара черные},

B₃ = {один белый, один черный шар}.

Очевидно, что события B₁, B₂ и B₃ несовместны и образуют полную группу. Их вероятности равны

, ,.

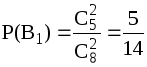Условные вероятности события А={шары одного цвета}, равны

, ,

.

Применяя формулу полной вероятности, получим

.