3.2. Вероятность суммы событий

Пусть А и В – два несовместных события. Тогда в соответствии с третьей аксиомой для вероятности имеем

P(A+B) = P(A) + P(B). (3.6)

Это равенство известно как теорема сложения вероятностей несовместных событий. Для классической схемы это свойство не нужно постулировать, т.к. легко выводится из классического определения вероятности (доказать самостоятельно).

Пример 3.5. Из колоды в 36 карт наугад вынимают 3 карты. Найти вероятность того, что среди них окажется хотя бы один туз.

Решение. Введем следующие события: B={появление хотя одного туза}, A₁={появление одного туза}, A₂={появление двух тузов}, A₃={появление трех тузов}. Очевидно, что B=A₁+A₂+A₃. Поскольку события A₁, A₂ и A₃.несовместны, то

P(B) = P(A₁)+P(A₂)+P(A₃) =

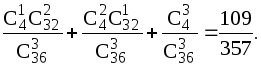
Эту задачу можно решить иначе. Событие , противоположное событию В, состоит в том, что среди вынутых из колоды трех карт нет ни одного туза. ПосколькуP(B)+P()=1, то

P(B) = 1 – P() =

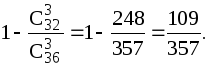
Пусть А и В – два произвольных события, т.е. они, в общем случае, совместны. Запишем события А+В и В в виде

A+B = A+Bи B = B+BA.

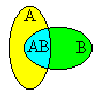
(объясните эти равенства, используя диаграммы Вьенна). Поскольку событие, стоящие в правых частях этих равенств, несовместны, то

P(A+B) = P(A) + P(B), P(B) = P(B)+P(BA).

Исключая P(B),получим

P(A+B) = P(A)+P(B)–P(AB). (3.7)

Это равенство известно как теорема сложения вероятностей совместных событий.

Полученная формула сложения вероятностей хорошо иллюстрируется при помощи диаграмм Вьенна. Здесь следует помнить, что вероятность события пропорциональна площади фигуры, которая соответствует данному событию. Событию А+В на рисунке соответствует вся заштрихованная фигура, площадь которой можно представить в виде суммы трех слагаемых S_A+B=S₁+S₂+S_AB, где S₁ соответствует событию А–АВ, а S₂ – событию В–АВ. Тогда, событию А будет соответствовать фигура с площадью S_А= S₁+S_АВ, а событию В – S_В= S₂+S_АВ. В результате получим, что S_А+В= S_А+S_В–S_АВ. Полученное равенство соответствует теореме сложения вероятностей.

Теорему сложения вероятностей можно обобщить на случай произвольного числа слагаемых. В частности,

P(A+B+C) = P(A)+P(B)+P(C)–(AB)–P(AC)–P(BC)+P(ABC). (3.8)

Докажите данную формулу самостоятельно.

Пример 3.6. Два стрелка делают по одному выстрелу по мишени. Вероятность попадания для первого стрелка равна 0,8, для второго – 0,7. Какова вероятность поражения цели?

Решение. Пусть A₁={первый стрелок попал по цели}, A₂={второй стрелок попал по цели}. Мишень будет поражена (событие В), если произойдет событие А₁+А₂. Поскольку события А₁ и А₂ совместны, но независимы, то

P(А₁+А₂) = P(А₁)+P(А₂)–P(А₁)P(А₂) = 0,7+0,8–0,70,8 = 0,94.

Отметим, что событие В можно записать также в виде A₁+A₂+A₁A₂. Тогда получим

P(B) = P(A₁)P()+P()P(A₂)+P(A₁)P(A₂) = = 0,80,3+0,20,7+0,70,8 = 0,94.

Однако такой путь слишком длинный.

Пример 3.7. Дана электрическая цепь:

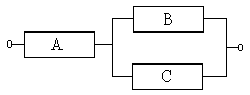
Вероятность выхода из строя элемента А равна 0,1, элемента В – 0,2, элемента С – 0,3. Найти вероятность разрыва цепи.

Решение. В данном случае разрыв цепи произойдет только тогда, когда выйдет из строя элемент А, или сразу два элемента В и С. При помощи алгебры событий разрыв цепи можно описать следующим образом: . Поскольку эти события совместные и независимые, то получим

= .