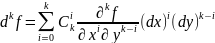- •(Алина) Первообразная и неопределенный интеграл (определения, свойства).
- •(Карина) Интегрирование по частям и замена переменной.
- •(Геля) Интегрирование рациональных функций.
- •(Алина) Интегрирование иррациональных функций , биномиальный дифференциал, подстановки Эйлера).
- •(Карина) Интегрирование функций, содержащих тригонометрические.
- •(Геля) Интеграл Римана: определение, необходимое условие интегрируемости по Риману.
- •(Алина) Суммы Дарбу и их свойства.
- •(Карина) Критерий интегрируемости по Риману.
- •(Геля) Достаточные условия интегрируемости по Риману.
- •(Алина) Свойства интеграла Римана.
- •(Карина) Интеграл с переменным верхним пределом, свойства. Формула Ньютона-Лейбница.
- •(Карина) Пространство Rn (скалярное произведение, норма, метрика).
- •(Геля) Предел последовательности в Rn: свойства, критерий Больцано-Коши, теорема Больцано-Вейерштрасса.
- •(Алина) Открытые и замкнутые множества в Rn.
- •(Карина) Предел функции.
- •(Геля) Повторные пределы.
- •(Алина) Непрерывность функции в точке.
- •(Карина) Линейно-связные множества и теорема Больцано-Коши о нуле.
- •(Геля) Компактность и теорема Вейерштрасса.
- •(Алина) Равномерная непрерывность.
- •(Карина) Частные производные, дифференцируемость, дифференциал.
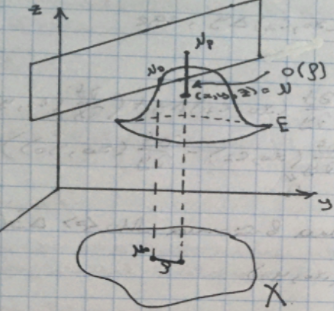
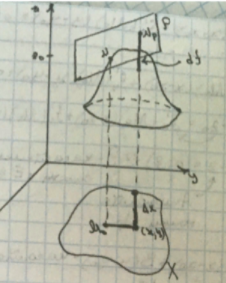
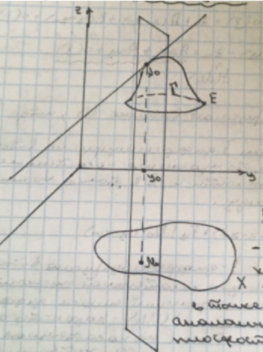
- •(Геля) Геометрический смысл дифференцируемости, дифференциала и частных производных.
- •(Алина) Производная сложной функции.
- •(Карина) Производная по направлению и градиент.
- •(Геля) Частные производные высших порядков, независимость смешанных производных от порядка дифференцирования.
- •(Алина) Дифференциалы высших порядков.
- •(Карина) Формула Тейлора.
- •(Геля) Экстремумы (необходимое условие, достаточное условие, следствие для функций двух переменных).
- •(Алина) Неявные функции, теорема об обратной функции.
- •(Карина) Условные экстремумы, метод множителей Лагранжа.
(Геля) Геометрический смысл дифференцируемости, дифференциала и частных производных.

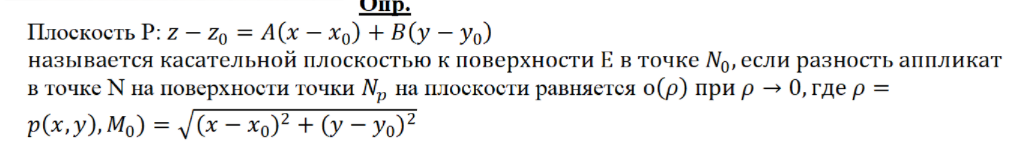


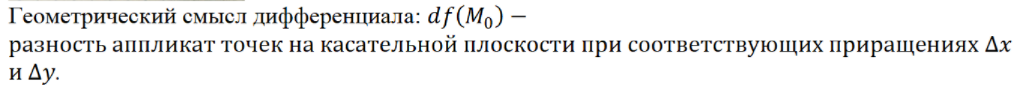

(Алина) Производная сложной функции.
1
переменная:f(g(x))'=f '(g(x))*g'(x).
n=2.
f(x,y)
опр. в области X ⊂
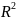 .
.
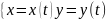 , t ∈ (a,b).
, t ∈ (a,b).
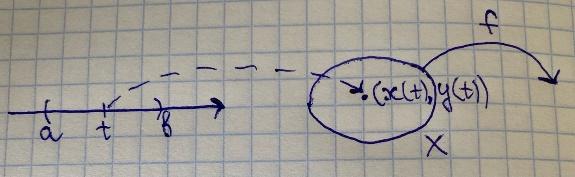 (x(t),y(t))
∈ X.
Рассмотрим h(t)=f(x(t),y(t))(функция 1
переменной): t ∈ (a,b)
(x(t),y(t))
∈ X.
Рассмотрим h(t)=f(x(t),y(t))(функция 1
переменной): t ∈ (a,b)
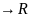 .
Теорема
1.
Если x(t),y(t) диф. в
.
Теорема
1.
Если x(t),y(t) диф. в
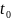 ∈ (a,b), f(x,y) диф. в т.
∈ (a,b), f(x,y) диф. в т.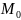 =(x(
),y(
)),
то h диф. в т.
и
h'(
)
=
=(x(
),y(
)),
то h диф. в т.
и
h'(
)
=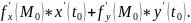 Доказательство:
Зададим
Δt в точке
.
f(x,
Доказательство:
Зададим
Δt в точке
.
f(x,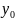 )
)
 ,
получат приращения Δx,Δy.
h'(
)=
,
получат приращения Δx,Δy.
h'(
)=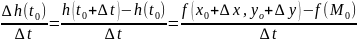
![]() Δf(
)
=
f диф. в точке
Δf(
)=
Δf(
)
=
f диф. в точке
Δf(
)=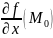 Δx+
Δx+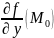 Δy+
Δy+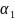 Δx+
Δx+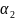 Δy,
где
,
.
=
+
Δy,
где
,
.
=
+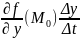 +
+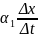 +
+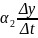 =
=
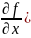 )x’(
)+
)x’(
)+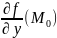 y’(
).
Ч.т.д.
n>=2.
y’(
).
Ч.т.д.
n>=2.
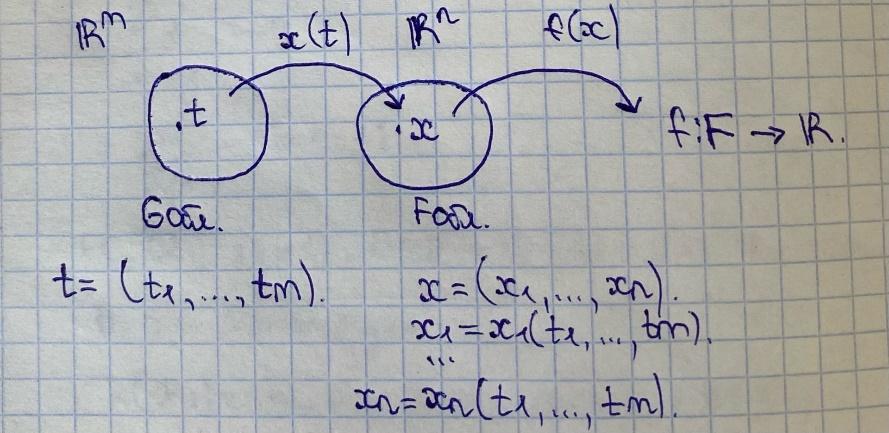 t=(
t=(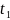 ,…,
,…,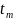 ).
x=(
).
x=(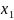 ,…,
,…,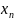 ).
=
(
,…,
).
…
=
(
,…,
).
Рассмотрим
h(t)=f(x(t)),т.е.
f(
,…,
).
=
(
,…,
).
…
=
(
,…,
).
Теорема
2.
Если
диф. в
∈ G. ∀
).
=
(
,…,
).
…
=
(
,…,
).
Рассмотрим
h(t)=f(x(t)),т.е.
f(
,…,
).
=
(
,…,
).
…
=
(
,…,
).
Теорема
2.
Если
диф. в
∈ G. ∀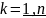 f
диф. в точке
=x(
),
то h диф. в точке
и
f
диф. в точке
=x(
),
то h диф. в точке
и
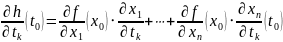 .
Без
док.-ва.
Следствие(инвариантность
формы первого дифференциала).
Вид
диф.-ла функции f(
,…,
)
не зависит от того, является ли
,…,
независимыми переменными или
функция.
.
Без
док.-ва.
Следствие(инвариантность
формы первого дифференциала).
Вид
диф.-ла функции f(
,…,
)
не зависит от того, является ли
,…,
независимыми переменными или
функция.
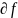 =
=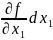 +…+
+…+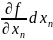 .(1)
Док.-во:
а)Если
,…,
-независимые
переменные
(1)-верно.
б)Пусть
=
(
,…,
).
…
=
(
,...,
).
df(x(t))=
.(1)
Док.-во:
а)Если
,…,
-независимые
переменные
(1)-верно.
б)Пусть
=
(
,…,
).
…
=
(
,...,
).
df(x(t))=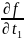 *
*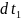 +…+
+…+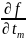 *
*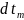 =
=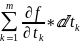 =
=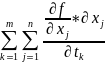 *
*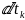 =
=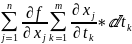 =(1).
Ч.т.д.
=(1).
Ч.т.д.
(Карина) Производная по направлению и градиент.



f(x,y)
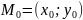
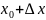
f
– дифференцируема в точке
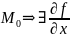 (
(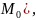
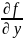 (
(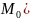
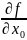 (
(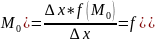
Движение вдоль Oy

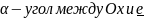
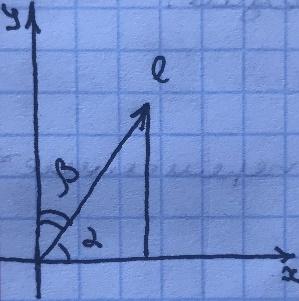
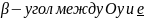
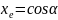
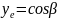
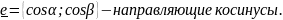
||e||=1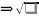
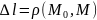
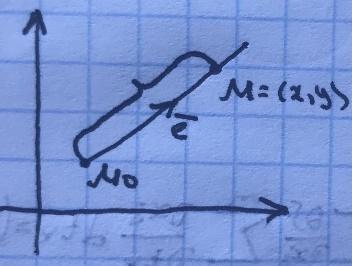
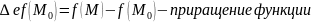
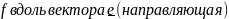
Опр.
Если существует
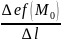 ,
то он называется производной по
направлению
,
то он называется производной по
направлению
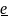 функции f в точке
функции f в точке
Обозначение:
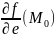
Теорема 1:
Если
f дифференцируема в точке
,
то
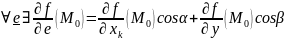
Д:
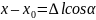
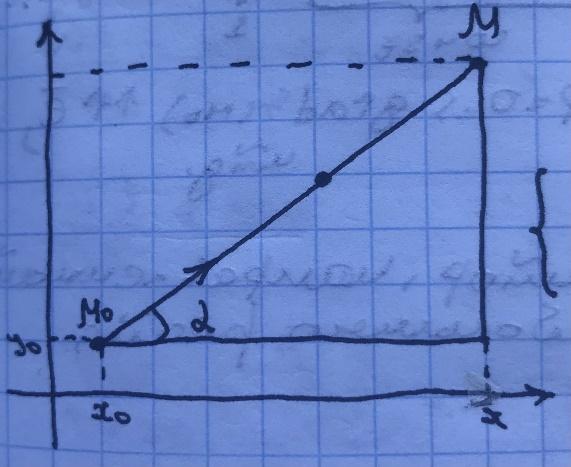
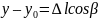
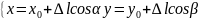
f(x,y)=f(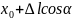 ,
,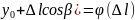 ,
,
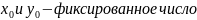
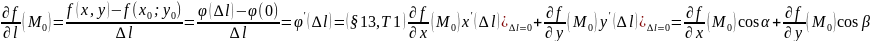 ,
чтд.
,
чтд.
Опр.
Градиентом функции f в точке
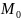 называется вектором
называется вектором
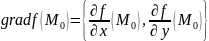
Следствие
(Т1):
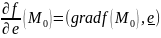
Теорема 2:
Пусть
f – дифференцируема в точке
,
тогда
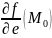 наибольшая если
наибольшая если
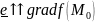 (одинаково
направлены)
(одинаково
направлены)
Д:
=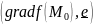 =
=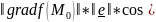 ,
,
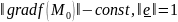 ,
,
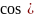
Наибольшее,
если cosφ=1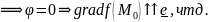
Следствие:
gradf(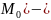 вектор
направленный сторону наибольшего роста
функции.
вектор
направленный сторону наибольшего роста
функции.
(Геля) Частные производные высших порядков, независимость смешанных производных от порядка дифференцирования.

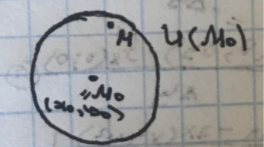
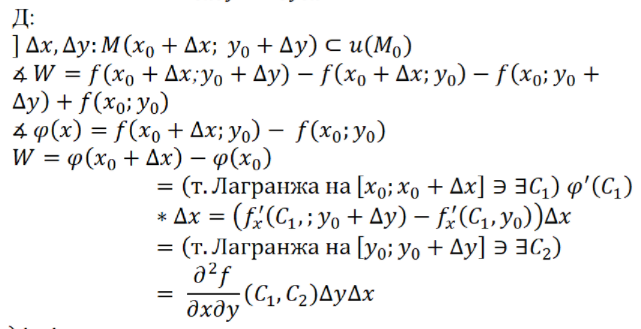
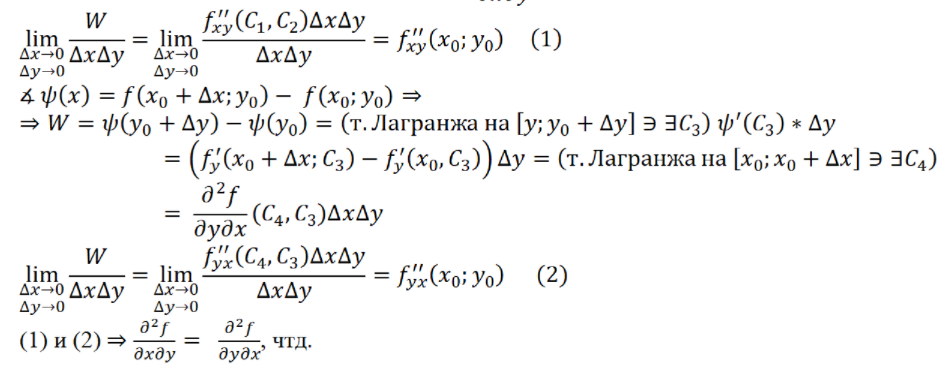

(Алина) Дифференциалы высших порядков.
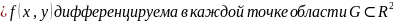
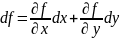
Зададим
новые приращения
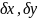 и вычислим дифференциал от
и вычислим дифференциал от
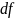 :
:
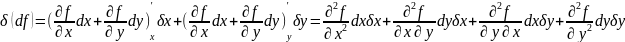
Будем считать, что производные второго порядка существуют, а смешанные непрерывны
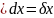
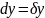
Опр. Дифференциал от первого дифференциала, вычисленный с теми же приращениями называют дифференциалом второго порядка функции f
Обозначают:
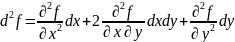
Опр. Дифференциал от дифференциала k-1–го порядка, вычисляемый с теми же приращениями, что и предыдущий, называется дифференциалом k–го порядка функции f.
Обозначают:
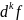
Опр.
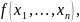 если у функции существуют все частные
производные до k-1–го порядка включительно,
дифференцируемы в точке
,
то
если у функции существуют все частные
производные до k-1–го порядка включительно,
дифференцируемы в точке
,
то
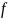 называется k раз дифференцируемой в
точке
называется k раз дифференцируемой в
точке
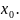 Если при этом все частные производные
k–го порядка непрерывны в точке
,
то
называется k раз непрерывно-дифференцируемой
в точке
Если при этом все частные производные
k–го порядка непрерывны в точке
,
то
называется k раз непрерывно-дифференцируемой
в точке
Теорема:
Если дифференцируема в каждой точке области D, тогда