2080

и вещество, является одним из видов материи, которой присущи масса и определенная энергия.

Таким обрезом, взаимодействие между электрическими зарядами осуществляется через электрическое поле.

Поле, создаваемое неподвижными электрическими зарядами, называют электростатическим. В данной главе будем изучать электростатическое поле, которое характеризуется двумя величинами: напряженностью и потенциалом.

13.1.4. Напряженность электростатического поля

Электрическое поле изучают с помощью пробного точечного положительного заряда такой малой величины, что он своим действием не искажает заметно исследуемое поле. Для этого можно, например, воспользоваться заряженным легким шариком, подвешенным на шелковой нити. Помещая пробный заряд в те или иные точки поля, можно определить действующие на него силы, которые в различных точках оказываются различными по величине и направлению.

Пусть на заряд q0 в данной точке поля действует сила F. Величина и направление этой силы зависят как от свойств поля в данной точке пространства, так и от величины пробного заря-

да q0. Однако если взять отношение F q0

не зависящую от размеров заряда. Это отношение является си-

ловой характеристикой поля, обозначается буквой E и называется напряженностью электрического поля. Таким образом, на-

пряженность поля

есть векторная физическая величина, характеризующая силовое воздействие поля на внесенный в него электрический заряд и численно равная силе, действующей на единичный положитель-

231

ный неподвижный заряд в данной точке поля. Из определения напряженности следует, что на любой заряд q, помещенный

При этом сила совпадает по направлению с напряженностью, если q > 0, и направлена против напряженности, если q < 0.

Из закона Кулона (см. формулу (13.1)) непосредственно следует, что напряженность поля, создаваемого неподвижным точечным зарядом q, на расстоянии r от него будет следующей:

где rr – единичный вектор в направлении напряженности E.

В скалярной форме

Опыт показывает, что напряженность поля систем точечных неподвижных зарядов равна векторной сумме напряженностей полей, создаваемых каждым из зарядов в отдельности:

Еi – напряженность поля, создаваемого зарядом qi на расстоянии ri от интересующей нас точки поля.

Это утверждение называют принципом суперпозиции (наложения) электрических полей. Он позволяет вычислять напря-

женность поля любой системы точечных зарядов, вклад каждого из которых дается формулой (13.8).

232

Если электрическое поле создается не системой точечных зарядов, а заряженным изотропным телом (заряд распределен по поверхности или в объеме), то это тело можно разбить на столь малые части, что каждая из них будет представлять собой точечный заряд dq. Таким образом, непрерывно распределенный заряд можно свести к системе дискретных бесконечно малых точечных зарядов, напряженность поля которых определяется выражением

Если заряды непрерывно распределены вдоль некоторой линии l, поверхности S или в объеме V, то вводят понятие соответственно линейной, поверхностной и объемной плотностей зарядов.

Линейная плотность зарядов

где dq – заряд бесконечно малого участка линии длиной dl. Поверхностная плотность зарядов

где dq – заряд малого участка поверхности площадью ds. Объемная плотность зарядов

где dq – заряд малого объема dV.

Для решения практических задач необходимо знать величину и направление напряженности в каждой точке поля. В этом случае удобно пользоваться графическим изображением электростатических полей, предложенным М. Фарадеем. Электрическое поле изображается с помощью силовых линий.

233

Силовыми линиями называются кривые касательные, к которым в каждой точке совпадают с направлением вектора напряженности поля (рис. 13.2). Силовым линиям приписывается направление: силовые линии начинаются на положительных зарядах и оканчиваются на отрицательных. Линии напряженности не пересекаются, так как в каж-

дой точке поля вектор Е имеет Рис. 13.2 только одно направление. Линии напряженности могут начинаться или заканчиваться лишь на зарядах, либо уходить в бесконечность, т.е. источником поля является заряд. Таким образом, электростатическое поле харак-

теризуется разрывными силовыми линиями.

Силовые линии проводятся с такой густотой, чтобы число линий, пронизывающих воображаемую площадку в 1 м2, перпендикулярную этим линиям, было равно напряженности поля в этом месте. Тогда по графическому изображению электрического поля можно судить не только о направлении, но и о значении напряженности поля.

Электрическое поле называется однородным, если оно изо-

бражается системой параллельных линий одинаковой густоты

(рис. 13.3, а). В противном случае поле называется неоднородным. На рис. 13.3, б, в приведены силовые линии положительно и отрицательно заряженных точечных зарядов.

Рис. 13.3

234

Силовые линии не следует отождествлять с траекториями движения в электростатическом поле очень легких заряженных частиц. Траектория частицы обладает тем свойством, что в каждой ее точке по касательной к ней направлена скорость частицы. По касательной же к силовой линии направлена сила, действующая со стороны поля на частицу, а следовательно, ускорение частицы.

13.2. Работа по перемещению заряда в электрическом поле. Потенциальная энергия, потенциал, разность потенциалов

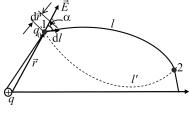
На всякий заряд, находящийся в электрическом поле, действует сила, которая может перемещать этот заряд. Определим работу А, совершаемую при перемещении пробного заряда q0 из

где α – угол между направлениями векторов F (или E ) и dl ; А – работа переноса заряда q0 из точки 1 в точку 2,

может быть положительной и отрицательной в зависимости от знака cosα.

235

Пусть поле создается положительным зарядом q. Тогда работа, совершаемая при перемещении заряда q0 из точки 1 в точку 2 в этом поле, запишется так (см. формулу (13.7)):

A = q0 4πεqεr2 dlcosα.

0

где r1, r2 – расстояния точек 1 и 2 от заряда q, создающего поле. Из формулы (13.15) видно, что работа, совершаемая при перемещении заряда в электростатическом поле, не зависит от формы и размеров пути, по которому движется заряд q0, а зависит только от начального и конечного положений этого заряда, диэлектрической проницаемости среды ε и величины зарядов q и q0. Следовательно, электростатические силы являются консер-

вативными, а поле – потенциальным.

Действительно, работа, которую совершают силы электростатического поля, перемещая единичный положительный заряд по замкнутому пути

Этот интеграл называется циркуляцией напряженности вдоль замкнутого контура.

В случае замкнутого пути начальная и конечная его точки совпадают. Поэтому из формулы (13.16) работа по перемещению заряда вдоль любого замкнутого контура равна нулю, т.е.

Силовое поле, которое удовлетворяет условию (13.17), называется потенциальным. Следовательно, электростатическое поле – потенциальное. Только в потенциальном поле можно ввести

236

понятие потенциала, являющегося энергетической характеристикой электростатического поля.

Потенциал ϕ – скалярная физическая величина, характеризующая энергию, которой обладает заряд, помещенный в данную точку поля, и численно равная потенциальной энергии единичного положительного заряда в этой точке поля:

Следовательно, потенциал ϕ данной точки поля численно равен работе, которую нужно совершить, чтобы переместить единичный положительный заряд из бесконечности в данную точку поля (если поле создается положительным зарядом).

Под «бесконечностью» понимается область пространства, столь далекая от всех электрических зарядов, что в этой области поле отсутствует (потенциал равен нулю). Следует отметить, что выбор нулевого потенциала не обязательно связывают с бесконечностью. Так, в электротехнике нулевым потенциалом обычно считается потенциал Земли.

Перемещая заряд q0 из данной точки поля (r1 = r) на бесконечность (r2 → ∞), силы поля совершают работу (cм. формулу

(13.15))

A = qq0 . 4πε0εr

Отсюда, воспользовавшись выражением (13.19), находим потенциал данной точки поля:

Работа, совершаемая электрическими силами при перемещении заряда q0 между двумя точками поля, равна произведению этого заряда на разность потенциалов в начальной и конечной точках пути.

Из выражения (13.23) видно:

1)что работа при перемещении заряда по замкнутому контуру равна нулю (ϕ1 = ϕ2);

2)работа сил поля положительна, когда +q0 заряд переме-

щается в направлении убывания потенциала (ϕ1 > ϕ2). Электростатическое поле можно графически изобразить

при помощи не только силовых линий, но и поверхностей равного потенциала или эквипотенциальных поверхностей.

Эквипотенциальной поверхностью называется геометрическое место точек с одинаковым потенциалом (ϕ = const). Ра-

бота, совершаемая при перемещении заряда вдоль такой поверхности, согласно (13.23) равна нулю. Это возможно, если

рактеризуется двумя физическими величинами – напряженно-

стью E и потенциалом ϕ. Очевидно, что между этими величинами должна существовать определенная связь, позволяющая одну величину находить через другую. Для нахождения этой связи запишем выражение для работы по перемещению заряда q0 на бесконечно малом отрезке пути dl через напряженность поля:

239

dA = q0 Edlcosα = q0 El dl,

где El = Ecosα – проекция вектора Е на перемещение dl , и через изменение потенциала поля (см. (13.23)),

dA = q0 (ϕ1 − ϕ2 ) = − q0dϕ,

где ϕ1 и ϕ2 – потенциалы двух бесконечно близких точек поля. Так как dϕ = ϕ2 – ϕ1, в последнем выражении появляется знак минус. Сравнивая две последнее формулы для dA, находим, что

Так как l – любое направление в пространстве, то в частности вдоль осей координат x, y, z связь напряженности с потенциалом запишется так:

где – оператор Лапласа.

Таким образом, напряженность поля в данной точке равна по величине и противоположна по направлению градиенту потенциала. Направление градиента совпадает с направлением нормали n (внешней нормали) к эквипотенциальной поверхности. В этом направлении при смещении из данной точки потенциал изменяется с наибольшей скоростью.

240