2080

5. ЭЛЕМЕНТЫ МЕХАНИКИ СПЛОШНЫХ СРЕД

Рассматриваемые вопросы. Общие свойства жидкостей и газов. Идеально упругое тело. Упругие напряжения и деформации. Закон Гука. Модуль Юнга.

5.1. Общие свойства жидкостей и газов

Любой объем жидкости или газа может как угодно изменять свою форму под действием сколь угодно малых сил. Это общее свойство жидкостей и газов является вместе с тем и их общим отличием от твердых тел. Однако для изменения самого объема жидкости или газа, так же как и в случае твердых тел, необходимы конечные внешние силы. Это значит, что при изменении объема жидкости или газа в нем возникают силы, в итоге уравновешивающие действие внешних сил. Известно, что под действием малых сил изменение формы жидкости или газа может происходить очень медленно; но оно всегда будет происходить до тех пор, пока действуют внешние силы. Подтверждением этому может служить произвольное движение твердого тела в жидкости или газе. Движение тела в жидкости или газе связано с изменением взаимного расположения отдельных частей жидкости или газа. Между тем это движение возникает под действием каких угодно малых сил.

Жидкости и газы ведут себя как упругие тела только в отношении изменения объема. Из двух элементарных деформаций – сжатия (растяжения) и сдвига – только первая связана с изменением объема. Поэтому только в отношении деформаций сжатия и растяжения жидкости и газы ведут себя, как упругие тела. Однако и в отношении этой деформации есть существенное различие в поведении жидкостей и газов, с одной стороны, и твердых тел – с другой.

91

Твердое тело можно растянуть и сжать в каком-либо одном направлении. Его можно также сжать во всех направлениях, т.е. подвергать всестороннему сжатию или растяжению. В жидкостях и газах практически приходится иметь дело только со всесторонним сжатием. Правда, в специальных условиях жидкость может быть подвергнута растяжению; при этой деформации

вней также возникают силы, подобные упругим силам в твердом теле. Но в задачах механики эти специальные условия обычно не возникают, и поэтому практически приходится иметь дело только с всесторонним сжатием в жидкости. Что же касается газов, то в них принципиально имеют место только деформации сжатия. Какой бы объем ни занимала данная масса газа, газ всегда оказывается сжатым, так как в отсутствие внешних сил объем газа будет увеличиваться беспредельно. Между тем жидкость в отсутствие внешних сил занимает определенный объем.

Общая черта жидкостей и газов состоит в том, что только

вотношении деформации всестороннего сжатия они ведут себя, как упругие тела. При сжатии жидкости или газа в них, как и

втвердом теле, возникают упругие силы, определяемые величиной деформации, т.е. степенью сжатия жидкости или газа. Если бы мы все деформации жидкости относили к нормальному ее состоянию, то мы всегда встречались бы с деформациями одного знака (сжатием). Как сказано, для газа такое нормальное, несжатое состояние вообще не имеет смысла вводить. Рассматривая же определенную степень сжатия газа как нормальное состояние, мы встретимся и с увеличением, и с уменьшением степени его сжатия, т.е. с деформациями различных знаков. Точно так же и для жидкости часто удобно определенную степень сжатия рассматривать как «нормальное» состояние и вводить деформации различных знаков. Формально все будет обстоять так же, как с упругими телами: можно говорить о сжатии и о «растяжении» жидкости или газа, хотя фактически речь идет лишь о разной степени сжатия.

92

Изменениям формы, не связанным с изменением объема, соответствует элементарная деформация сдвига. При быстрых деформациях сдвига в жидкости и газе могут возникать заметные силы. Однако эти силы зависят не от величины деформации, а от скорости изменения деформации. И если скорость деформаций стремится к нулю, то и силы стремятся к нулю. Поэтому эти силы следует рассматривать не как упругие силы, а как силы трения. Эти силы внутреннего трения называют силами вязкости. С силами вязкости приходится считаться только при рассмотрении достаточно быстрых движений, когда сдвиги в жидкости или газе изменяются с достаточно большой скоростью. Какая скорость окажется «достаточно большой» в этом смысле, зависит от свойств жидкости или газа и конкретных условий задачи. Но во всяком случае для всех конкретных условий можно указать столь медленные движения, при которых с силами, возникающими в жидкости и газе при сдвигах, можно не считаться. Разумеется, с этими силами можно не считаться при рассмотрении задач о равновесии жидкостей и газов. Молекулы газа вследствие беспорядочного и хаотического движения не связаны или слабо связаны силами взаимодействия, поэтому они движутся свободно, в результате соударений стремятся разлететься во все стороны, заполняя весь предоставленный им объем, т.е. объем газа определяется объемом того сосуда, который газ занимает.

Жидкость, как и газ, принимает форму сосуда, в котором она находится. Но в жидкости, в отличие от газа, среднее расстояние между молекулами остается постоянным, поэтому она обладает неизменным объемом.

Хотя свойства жидкостей и газов во многом отличаются, в ряде механических явлений их поведение определяется одинаковыми параметрами и идентичными уравнениями. Поэтому гидроаэромеханика – раздел механики, изучающий равновесие и движение жидкостей и газов, их взаимодействие между собой и

93

обтекаемыми ими твердыми телами, − использует единый подход к изучению жидкостей и газов.

В механике жидкости и газы рассматриваются как сплошные, непрерывно распределенные в занятой ими части пространства. Плотность жидкости мало зависит от давления. Плотность же газов от давления зависит существенно. Из опыта известно, что сжимаемостью жидкости и газа во многих задачах можно пренебречь и пользоваться единым понятием несжимаемой жидкости, т.е. жидкости, плотность которой всюду одинакова и не изменяется со временем.

Если в покоящуюся жидкость поместить тонкую пластинку, то части жидкости, находящиеся по разные стороны от нее, будут действовать на каждый ее элемент S с силами F. Эти силы независимо от того, как пластинка ориентирована, будут равны по модулю и направлены перпендикулярно S, так как наличие касательных сил привело бы частицы жидкости в движение.

Физическая величина, определяемая нормальной силой, действующей со стороны жидкости на единицу площади, называется давлением жидкости р:

p= F S.

Единица измерения давления − паскаль (Па): 1 Па равен давлению, создаваемому силой 1 Н, равномерно распределенной по нормальной к поверхности площади 1 м2, 1 Па = 1 Н/м2.

Давление при равновесии жидкостей (газов) подчиняется закону Паскаля: давление в любом месте покоящейся жидкости одинаково по всем направлениям, причем давление одинаково передается по всему объему, занятому данной жидкостью.

Рассмотрим влияние веса жидкости на распределение давления внутри несжимаемой жидкости, находящейся в состоянии покоя. При равновесии жидкости давление по горизонтали всегда одинаково, иначе не было бы равновесия. Поэтому свободная поверхность жидкости в состоянии покоя всегда горизон-

94

тальна вдали от стенок сосуда. Если жидкость несжимаема, то ее плотность не зависит от давления. Тогда при поперечном сечении S столба жидкости, его высоте h и плотности ρ вес жидкости Р = ρgSh, а давление на нижнее основание:

т.е. давление изменяется линейно с высотой. Давление ρgh называется гидростатическим.

Согласно формуле (5.1) сила давления на нижние слои будет больше, чем на верхние, поэтому на тело, погруженное в жидкость (газ), действует выталкивающая сила, определяемая законом Архимеда: на тело, погруженное в жидкость (газ), действует со стороны этой жидкости (газа) направленная вверх выталкивающая сила, равная весу вытесненной телом жидкости (газа):

где ρ − плотность жидкости; V – объем погруженного в жидкость тела.

5.2.Идеально упругое тело. Упругие напряжения

идеформации. Закон Гука. Модуль Юнга

Под действием внешних сил возникают деформации тел. Если после прекращения действия сил восстанавливаются форма и размеры тела, то деформация называется упругой. Деформация имеет упругий характер, если внешняя сила не превосходит предела упругости. При превышении этого предела деформация становится пластической. В этом случае после устранения внешних сил форма и размеры тела полностью не восстанавливаются.

Закон Гука – уравнение теории упругости, связывающее напряжение и деформацию упругой среды открыт в 1660 году английским ученым Робертом Гуком (англ. Robert Hooke). По-

95

скольку закон Гука записывается для малых напряжений и деформаций, он имеет вид простой пропорциональности. В словесной форме закон звучит следующим образом: «Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации».

Для тонкого растяжимого стержня закон Гука имеет вид

l – абсолютное удлинение (сжатие) стержня; k – коэффициент упругости (или жесткости).

Коэффициент упругости зависит как от свойств материала, так и от размеров стержня. Можно выделить зависимость от размеров стержня (площади поперечного сечения S и длины L)

Величина Е называется модулем упругости первого рода или модулем Юнга и является механической характеристикой материала.

Если ввести относительное удлинение

и нормальное напряжение в поперечном сечении

В такой форме он справедлив для любых малых объемов материала.

96

Также при расчете прямых стержней применяют запись закона Гука в относительной форме

l = EFSL .

Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.

Модуль Юнга (модуль упругости) – физическая величина, характеризующая свойства материала сопротивляться растяжению (сжатию) при упругой деформации. Назван в честь английского физика XIX века Томаса Юнга. В динамических задачах механики модуль Юнга рассматривается в более общем смысле – как функционал среды и процесса. В Международной системе единиц (СИ) измеряется в ньютонах на метр в квадрате или в паскалях.

Модуль Юнга рассчитывается следующим образом:

где E – модуль упругости; F – сила; S – площадь поверхности, по которой распределено действие силы; l – длина деформируемого стержня; x – модуль изменения длины стержня в результате упругой деформации (измеренного в тех же единицах, что и длина l).

Через модуль Юнга вычисляется скорость распространения продольной волны втонком стержне:

с = Eρ ,

где ρ – плотность вещества.

97

6. РЕЛЯТИВИСТСКАЯ МЕХАНИКА

Рассматриваемыевопросы. Принцип относительности и преобразования Галилея. Неинвариантность электромагнитных явлений относительно преобразований Галилея. Постулаты специальной теории относительности (СТО) Эйнштейна. Относительность одновременности. Парадоксы релятивистской кинематики: сокращение длины и замедление времени

вдвижущихся системах отсчета.

6.1.Принцип относительности и преобразования Галилея. Неинвариантность электромагнитных явлений относительно преобразований Галилея

Сименем Г. Галилея связана подлинная революция в механике. Он ввел в механику точный количественный эксперимент и математическое описание явлений. Первостепенную роль в развитии представлений о пространстве сыграл открытый им общий принцип классической механики – принцип относительности Галилея.

Согласно этому принципу все физические (механические) явления происходят одинаково во всех системах, покоящихся или движущихся равномерно и прямолинейно с постоянной по величине и направлению скоростью. Такие системы называются инерциальными. Математические преобразования Галилея отражают движение в двух инерциальных системах, движущихся с относительно малой скоростью (меньшей, чем скорость света

ввакууме). Они устанавливают инвариантность (неизменность)

всистемах длины, времени и ускорения. Дальнейшее развитие представлений о пространстве и времени связано с рационалистической физикой Р. Декарта, который создал первую универсальную физико-космологическую картину мира. В основу ее Декарт положил идею о том, что все явления природы объясняются механическим воздействием элементарных материальных

98

частиц. Взаимодействием элементарных частиц Декарт пытался объяснить все наблюдаемые физические явления: теплоту, свет, электричество, магнетизм. Само же взаимодействие он представлял в виде давления или удара при соприкосновении частиц друг с другом и ввел таким образом в физику идею близкодействия.

Декарт обосновывал единство физики и геометрии. Он ввел координатную систему (названную впоследствии его именем), в которой время представлялось как одна из пространственных осей. Тезис о единстве физики и геометрии привел его к отождествлению материальности и протяженности. Исходя из этого тезиса он отрицал пустое пространство и отождествил пространство с протяженностью.

Декарт развил также представление о соотношении длительности и времени. Длительность, по его мнению, «присуща материальному миру. Время же – присуще человеку и потому является модулем мышления». «…Время, которое мы отличаем от длительности, – пишет Декарт в “Началах философии”, – есть лишь известный способ, каким мы эту длительность мыслим…».

Таким образом, развитие представлений о пространстве и времени в доньютоновский период способствовало созданию

и экспериментальное обоснование свойств пространства и времени в рамках классической механики.

Рассмотрим преобразование Галилея при переходе от одной инерциальной системы отсчета (ИСО) к другой. Пусть име-

Приняв за начало отсчета времени момент, когда начала координат O и O′ совпадали, запишем соотношения между координатами какой-либо точки P в системах K и K′ :

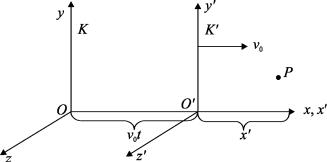
Рис. 6.1

Кроме того, считаем, что время в обеих системах течет одинаково, т.е. t = t′. Эти соотношения представляют собой

преобразования Галилея, справедливые только при движении тел со скоростями, много меньшими скорости света в вакууме c. Дифференцируя (6.1) по времени, находим классический закон сложения скоростей (закон преобразования скоростей):

Если это соотношение продифференцировать по времени, то найдем, что ускорение точки одинаково во всех ИСО a = a′. Кроме того, из второго закона Ньютона вытекает, что и силы, действующие на одно и то же тело, в ИСО одинаковы.

Отсюда следует вывод о том, что уравнения динамики инвариантны (не изменяются) при переходе от одной ИСО к другой. Или можно сказать иначе: никакими механическими опытами, проведенными внутри системы отсчета, невозможно определить движется ли данная система отсчета равномерно и прямолинейно или покоится. Данное утверждение носит название принципа относительности Галилея.

100