Глава 16. Обыкновенные дифференциальные уравнения

Уравнение, связывающее независимую переменную , функцию и ее производные , называется обыкновенным дифференциальным уравнением.

.

1. Порядок дифференциального уравнения

Наивысший порядок производной, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения.

Задача.

Укажите дифференциальное уравнение первого порядка (выберите несколько вариантов ответа).

Варианты ответов:

1) 2) 3) 4)

Решение.

1) Представим уравнение в виде ;

- уравнение первого порядка.

2) Содержит , поэтому является дифференциальным уравнением первого порядка.

3) Не содержит производных, поэтому не является дифференциальным уравнением.

4) Содержит , поэтому является дифференциальным уравнением второго порядка.

Ответ. №1, №2.

§1 Дифференциальные уравнения I порядка

2. Дифференциальные уравнения I порядка.

Уравнение вида или называется дифференциальным уравнением I порядка.

3. Решение дифференциального уравнения I порядка

Решением дифференциального уравнения первого порядка , называется дифференцируемая на некотором интервале функция , которая при подстановке в уравнение вместо неизвестной функции обращает его в тождество.

4. Общее решение дифференциального уравнения 1-го порядка

Общим решением дифференциального уравнения первого порядка называется функция , которая при любом значении произвольной постоянной является решением данного уравнения.

Построенный на плоскости график всякого решения данного дифференциального уравнения называется интегральной кривой этого уравнения.

Таким образом, общему решению на плоскости соответствует семейство интегральных кривых, зависящее от одного параметра – произвольной постоянной С.

5. Частные решения

Решения, которые получаются из общего решения при определенном значении произвольной постоянной С, называются частными.

Частные решения удовлетворяют начальным условиям (условиям Коши):

или .

Геометрически график частного решения – это интегральная кривая, проходящая через заданную точку плоскости .

§2 Типы дифференциальных уравнений первого порядка

6. Уравнения с разделяющимися переменными или

Разделить переменные и проинтегрировать полученные выражения

Задача.

Дано дифференциальное уравнение при . Тогда его решением является функция … .

Варианты ответов: 1) 2) 3) 4)

Решение.

- уравнение с разделяющимися переменными. Разделим переменные.

; ; ; ; ; .

, значит , . Тогда , . Тогда .

Ответ. №2.

Задача.

Дано дифференциальное уравнение , тогда функция является его решением при равном …

Варианты ответов: 1) 2 2) 3 3) 1 4) 0

Решение.

, , ; .

Сравнивая с , получаем, что , откуда .

Ответ. №1.

7. Однородное уравнение ,

где , - однородные функции одного порядка

Замена: ; ,

Задача.

Уравнение является… .

Варианты ответов: 1) уравнением Бернулли 2) однородным дифференциальным уравнением

3) уравнением с разделяющимися переменными 4) дифференциальным уравнением 1 порядка

Решение.

Уравнение перепишем в виде , т.е. в виде , значит, оно является однородным.

Ответ. №2.

Задача.

Найти общий интеграл уравнения .

Решение.

Функции , - однородные второго порядка.

Пусть , откуда , тогда

;

;

.

Разделим на .

.

; ; .

Так как , то ; .

Ответ. .

8. Линейное уравнение

Замена: ,

Задача.

Проинтегрировать уравнение: .

Решение.

Полагаем , тогда и уравнение примет вид

, .

Решим сначала уравнение .

, , .

Подставим и решим уравнение ,

, , . Тогда .

Ответ. .

9. Уравнение Бернулли

, ,

Замена: ,

Задача.

Выберите несколько вариантов ответов. Из данных дифференциальных уравнений уравнениями Бернулли являются:

Варианты ответов: 1) 2) 3) 4)

Решение.

Приведем уравнение к виду:

1) - линейное ДУ; 2) - ДУ с разделяющимися переменными;

3) - уравнение Бернулли; 4) - уравнение Бернулли.

Ответ. №3, №4.

10. Уравнения в полных дифференциалах , где

, .

1) проверить выполнение условия .

2) используя равенства , , найти функцию .

3) записать решение .

Задача.

Решить уравнение

.

Решение.

; . ; . .

Значит, , .

Отсюда

, , далее , .

, .

Ответ. .

§3 Дифференциальные уравнения высших порядков

11. Дифференциальные уравнения высших порядков

Дифференциальными уравнениями n-го порядка называются уравнения вида

.

12. Решение

дифференциальных уравнений

Решением дифференциального уравнения n-го порядка является n раз дифференцируемая функция , которая обращает данное уравнение в тождество.

13. Общее решение дифференциального уравнения

Функция называется общим решением дифференциального уравнения n-го порядка, если при любом выборе произвольных постоянных эта функция удовлетворяет начальным условиям

задача Коши.

14. Частное решение дифференциального уравнения

Всякое решение, получаемое из общего решения при конкретных значениях постоянных , называется частным решением этого уравнения.

15. Уравнения, допускающие понижение порядка

а) , n раз проинтегрировать

Задача.

Общее решение ДУ имеет вид … .

Варианты ответов: 1) 2) 3)

4)

Решение.

, ,

Ответ. №3

б) (нет у). Замена: , ,

Задача.

Общим решением дифференциального уравнения является … .

Варианты ответов: 1) 2) 3) 4)

Решение.

Сделаем замену: , . Получим уравнения: .

- уравнение с разделяющимися переменными. .

.

.

Т.к. , то , тогда , , где .

Ответ. №1.

в) (нет х). Замена: , ,

Задача.

Порядок дифференциального уравнения можно понизить заменой … .

Варианты ответов: 1) 2) 3) 4)

Решение.

Так как в уравнении нет х, то замена .

Ответ. №2.

§4 Линейные уравнения высших порядков

16. Линейные

дифференциальные уравнения n-го порядка (ЛНДУ)

(*)

Функции заданы и непрерывны в некотором промежутке .

Если , то уравнение называется линейным неоднородным.

Если , то уравнение (*) называется линейным однородным.

17. Общее решение ЛНДУ

Общим решением уравнения (*) является сумма его произвольного частного решения и общего решения соответствующего однородного уравнения , т.е.

18. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

,

- постоянные

Составить характеристическое уравнение

.

Вычислить дискриминант и корни характеристического уравнения.

Записать ответ, используя следующую таблицу.

Дискриминант

Корни

,

,

Фундаментальная

система частных решений

,

,

,

Общее решение

Задача.

Дано линейное однородное уравнение . Тогда общим решением является … .

Варианты ответов: 1) 2) 3) 4)

Решение.

Составим характеристическое уравнение

;

;

, , .

Значит, общим решением будет

.

Ответ. №2.

Задача.

Установите соответствие между ДУ и их характеристическими уравнениями:

1. ; 2. ; 3. .

Варианты ответов: А) В) С) D)

E)

Решение.

1) Уравнению соответствует характеристическое уравнение . (Е).

2) Уравнению соответствует характеристическое уравнение . (А).

3) Уравнению соответствует характеристическое уравнение . (В).

Ответ.

Задача.

Семейству интегральных кривых , где и произвольные постоянные, соответствует однородное дифференциальное уравнение второго порядка … .

Варианты ответов: 1) 2) 3) 4)

Решение.

Из выпишем корни характеристического уравнения: , .

По теореме Виета: . .

Соответствующее однородное дифференциальное уравнение второго порядка имеет вид: .

Ответ. №3.

Задача.

Общее решение линейного однородного дифференциального уравнения второго порядка с равными действительными корнями характеристического уравнения имеет вид… .

Варианты ответов: 1) 2) 3) 4)

Решение.

Так как корни характеристического уравнения равны , то общее решение дифференциального уравнения имеет вид: .

Ответ. №2.

19. ЛНДУ второго порядка. Метод вариации произвольных постоянных.

Для решения уравнения

(**)

необходимо:

1) найти общее решение ( ) ЛОДУ в виде

,

где - частные решения однородного уравнения,

- произвольные постоянные.

2) частное решение уравнения (**) записать в виде:

,

где - неизвестные функции.

3) составить систему

и решить ее относительно и .

4) проинтегрировав функции и , найти .

5) записать ответ в виде суммы общего решения соответствующего однородного уравнения и полученного частного решения :

20. ЛНДУ второго порядка с постоянными коэффициентами

со специальной правой частью

Для решения уравнения

,

необходимо:

1) найти общее решение ( ) ЛОДУ в виде

,

где , - частное решение однородного уравнения,

- произвольные постоянные.

2) по виду специальной правой части записать ожидаемую форму частного решения с неопределенными коэффициентами.

Вид правой части

Форма частного решения

I. ,

где - многочлен n-ой степени, .

I. ,

где - многочлен n-ой степени с неопределенными коэффициентами

,

- число, равное кратности корня как корня характеристического уравнения (т.е. число, показывающее, сколько раз является корнем уравнения)

.

II. ,

где , и - многочлены степени n и m соответственно.

II. ,

где - число, равное кратности как корня характеристического уравнения ,

и - многочлены степени с неопределенными коэффициентами,

- наивысшая степень многочленов и .

3) вычислить производные , и подставить , , в данное уравнение.

4) из полученного тождества найти значения неопределенных коэффициентов.

5) записать ответ в виде суммы общего решения соответствующего однородного уравнения и полученного частного решения :

Задача.

Частному решению линейного неоднородного дифференциального уравнения по виду его правой части соответствует функция … .

Варианты ответов: 1) 2) 3) 4)

Решение.

Решим однородное уравнение: .

Ему соответствует характеристическое уравнение

;

;

.

Тогда общее решение однородного уравнения имеет вид .

Частное решение ищем в виде:

.

, , .

Поэтому частное решение имеет вид: .

Ответ. №2.

Задача.

Если функция имеет вид: 1. 2. 3). 4) , то частное решение неоднородного дифференциального уравнения следует искать в виде …

Варианты ответов: А) В) С) D) E)

Решение.

Однородное уравнение имеет корни характеристического уравнения, равные , а, следовательно, общее решение . Тогда частное решение неоднородного дифференциального уравнения следует искать в виде

1) , так как содержит многочлены первой степени и , . (D).

2) , так как содержит многочлен второй степени и , . (Е).

3) , так как содержит многочлен нулевой степени и корень кратности 2 ( , ). (А).

4) , так как содержит многочлен нулевой степени и , . (С).

Ответ.

Задача.

Частное решение дифференциального уравнения имеет вид … .

Варианты ответов: 1) 2) 3) 4)

Решение.

Соответствующее уравнение имеет вид , его характеристическое уравнение , откуда , .

Т.е. ,

.

Тогда частное решение следует искать в виде

, , .

.

Ответ. №4.

§5 Системы дифференциальных уравнений

21. Системы

дифференциальных уравнений

22. Нормальная

система дифференциальных уравнений

Системой дифференциальных уравнений называется совокупность дифференциальных уравнений, каждая из которых содержит независимую переменную, искомые функции и их производные.

Система дифференциальных уравнений вида

где - неизвестные функции независимой переменной t, называется нормальной системой

Если правые части нормальной системы дифференциальных уравнений являются линейными функциями относительно , то система дифференциальных уравнений называется линейной.

Иногда нормальную систему дифференциальных уравнений удается свести к одному уравнению n-го порядка, содержащему одну неизвестную функцию. Сведение нормальной системы к одному уравнению может быть достигнуто дифференцированием одного из уравнений системы и исключением всех неизвестных, кроме одного (так называемый метод исключения).

Задача.

Система дифференциальных уравнений может быть сведена к уравнению вида…

Варианты ответов: 1)

2)

3)

4)

Решение.

Продифференцируем первое уравнение системы: .

Подставим второе уравнение системы в полученное уравнение:

.

Так как из первого уравнения системы , то получаем уравнения вида:

,

,

.

Ответ. №4.
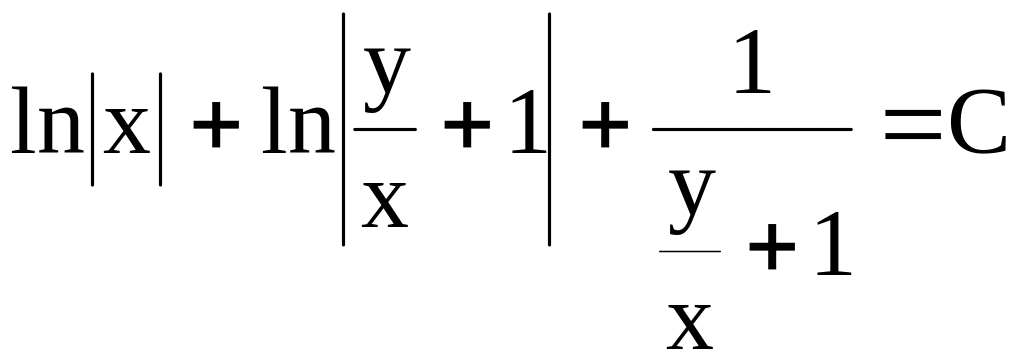