16. Механическая работа. Работа переменной силы.

Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек) тела или системы.

При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения:

Здесь точкой обозначено скалярное произведение,   — вектор перемещения; подразумевается, что действующая сила   постоянна в течение всего того времени, за которое вычисляется работа.

Если сила не постоянна, то в этом случае она вычисляется как интеграл:

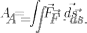
(подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений   если вначале считать их конечными, а потом устремить длину каждого к нулю).

Если существует зависимость силы от координат, интеграл определяется следующим образом:

,

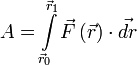где   и   — радиус-векторы начального и конечного положения тела соответственно.

• Cледствие: если направление движения тела ортогонально силе, работа (этой силы) равна нулю.

Работа переменной силы

   Пусть материальная точка перемещения под действием силы F, которая направлена вдоль оси Ох, имеет переменную величину, которая непрерывно зависит от х. Требуется определить работу А, совершаемую силой F, по перемещению материальной точки вдоль оси Ох из точки х = а в точку х = b ( а < b). Функция F(х) предполагается непрерывной на отрезке [ а, b].    Разобьем произвольно отрезок [а, b] на n частей точками а = х₀ < x₁ < x₂ < … < x_n = b. Выберем на каждом частичном отрезке [x _{i - 1}, x_i] точку ξ _i. Сила, действующая на материальную точку на отрезке [x _{i - 1}, x _i], изменяется от точки к точке. Но если длина отрезка мала, то значение силы в точках отрезка [x _{i - 1}, x_i] мало отличается от ее значения в любой точке ξ _i Î [x_{i - 1}, x_i], так как F (x) непрерывна. Поэтому работу А _i, совершаемую силой F на [x_{i - 1}, x_i] можно считать приближенно равной работе совершаемой на том же отрезке постоянной силой F(ξ _i ), т. е.

A_i ≈ F (ξ_i) Δx_i.

   Рассуждая аналогично для каждого отрезка разбиения, получаем приближенное значение работы А силы F на всем отрезке:

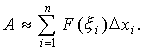
   С другой стороны, сумма в правой части равенства является интегральной суммой для функции F (x). Так как функция F (x ) непрерывна на отрезке [a, b], то предел этой суммы при

существует и равен определенному интегралу от функции F (x ) по отрезку [a, b]. Таким образом,

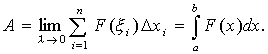
17) Принцип относительности в классической и релятивистской механике

классическая: Принцип относительности утверждает, что во всех инерциальных системах все механические процессы описываются одинаковым образом, т.е. посредством законов, имеющих ту же самую математическую форму. Иначе говоря, в таких системах законы движения тел описываются теми же самыми математическими уравнениями или формулами. 

релятивистская: В отличие от классической механики, в специальной теории относительности одновременность двух событий, происходящих в разных точках пространства, относительна: события, одновременные в одной инерциальной системе отсчёта, не одновременны в других инерциальных системах, движущихся относительно первой.

18) Энергия. Виды механической энергии

общая количественная мера движения и взаимодействия всех видов материи.

Энергия не возникает из ничего и никуда не исчезает, она может только переходить из одного вида в другой.

Понятие энергии связывает все явления природы в одно целое, является

общей характеристикой состояния физических тел и физических полей

Виды: механическая , электромагнитная , химическая , ядерная ,тепловая , гравитационная и др.

!!19) Основные понятия и величины динамики вращательного движения.

Основной закон динамики вращательного движения можно получить из второго закона Ньютона для поступательного движения твердого тела. Если к твердому телу массой m в точке А приложить силу F, то в результате жесткой связи между всеми материальными точками тела все они получат угловое ускорение  и соответственные линейные ускорения, как если бы на каждую точку действовала сила  . Для каждой материальной точки. ,                                                                                              

где  – момент силы – это произведение силы   на ее плечо  .

Плечом силы называют кратчайшее расстояние от оси вращения “ОО” до линии действия силы  .

20) Консервативные и неконсервативные силы и системы

консервативная: Силы, работа которых не зависит от формы траектории, а определяется только начальным и конечным размещением тела в пространстве.

- силы притяжения

- силы упругости

- электростатические силы взаимодействия между заряженными телами

неконсервативные: Эти силы зависят не только от формы тел, но и от их скорости. Они направлены всегда против направления скорости, потому работа сил трения всегда отрицательна.

- силы трения, которые возникают при скольжении одного тела по поверхности другого

- силы сопротивления, которых испытывает тело, двигаясь в жидкой или газообразной среде

!!21) Кинетическая энергия релятивистской частицы

частица, движущаяся с релятивистской скоростью, то есть скоростью, сравнимой со скоростью света. Движение таких частиц, рассматриваемых как классические (неквантовые) материальные точки, описывается специальной теорией относительности. Безмассовые частицы фотоны всегда являются релятивистскими, поскольку могут существовать, лишь двигаясь со скоростью света.

22) Связь между механической работой и энергией.

То тело, которое способно совершать работу, обладает энергией.

Механическая энергия идет на производство работы и плюс потери на нагревание окружающей среды

23) Момент силы относительно точки и относительно оси

Момент силы относительно точки О - это вектор, модуль которого равен произведению модуля силы на плечо - кратчайшее расстояние от точки О до линии действия силы. Направление вектора момента силы перпендикулярно плоскости, проходящей через точку и линию действия силы, так, что глядя по направлению вектора момента, вращение, совершаемое силой вокруг точки О, происходит по часовой стрелке

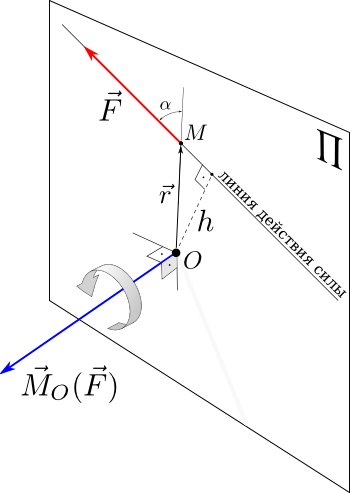
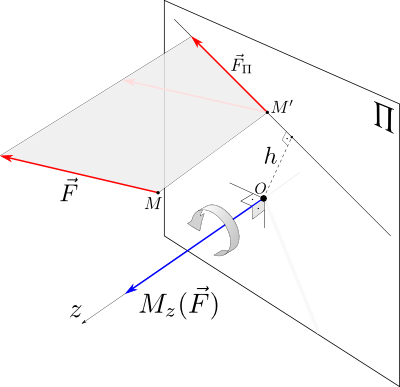
Момент силы относительно оси вычисляется как момент проекции силы F⃗ на плоскость Π, перпендикулярную оси, относительно точки пересечения оси с плоскостью. Знак момента определяется направлением вращения, которое стремится придать телу сила F⃗ Π. Если, глядя по направлению оси Oz сила вращает тело по часовой стрелке, то момент берется со знаком ``плюс'', иначе - ``минус''.

24) Момент инерции частицы и твёрдого тела относительно оси. Теорема Штейнера.

Теорема Штейнера. момент инерции тела   относительно произвольной оси равен сумме момента инерции этого тела   относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела   на квадрат расстояния   между осями:

где

 — известный момент инерции относительно оси, проходящей через центр масс тела,

 — искомый момент инерции относительно параллельной оси,

 — масса тела,

 — расстояние между указанными осями.

25) Момент импульса относительно точки и относительно оси.

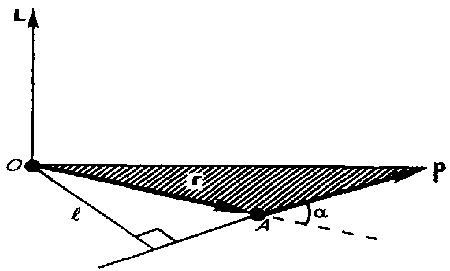
называется физическая величина, определяемая векторным произведением:

 

где r - радиус-вектор, проведенный из точки О в точку A, p=mv - импульс материальной точки, L - направление которого совпадает с направлением поступательного движения правого винта при его вращении от r к р.

называется скалярная величина, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси.