4.1 Системы счисления

Системой счисления (СС) называют совокупность цифровых знаков и правил их записи, применяемую для однозначного изображения чисел. Различают позиционные и непозиционные системы счисления.

В непозиционных системах счисления значение каждой цифры не зависит от ее позиции в числе. В настоящее время непозиционные сис­темы счисления применяются редко и в основном для целей нумерации.

Непозиционной системой счисления является римская система. В ней применяются следующие цифры:

десятичные числа: 1 5 10 50 100 500 1000 и т. д.;

римские цифры: I V X L C D M и т. д.

Десятичное число 32 изображается в римской системе счисления так:

XXXII = X+X+X+I+I=32,

то есть несколько стоящих рядом одинаковых цифр суммируются. Если рядом стоят две разные цифры, то они могут либо суммироваться, либо вычитаться, например

ХХVI = X + X + V + I = 26 и IX = X – I = 9.

Арифметические действия с числами в непозиционных системах сложны.

В ЭВМ преимущественное применение получили позиционные систе­мы счисления, в которых значение каждой цифры находится в строгой зависимости от ее позиции в числе.

Основанием системы счисления называют количество различных цифр, применяемых в данной позиционной системе счисления. Всем из­вестна с детства десятичная система счисления, в которой применя­ется десять цифр.

Десятичная система счисления – не единственная позиционная система. Возможны позиционные системы счисления с любым основанием в виде целого числа. Примеры систем счисления приведены в таблице.

Особый интерес при изучении вычислительной техники представляют двоичная, восьмеричная и шестнадцатеричная системы счисления (таблица 4.1).

Таблица 4.1

Основание	Система счисления	Цифровые символы
2	двоичная	0, 1
3	троичная	0, 1, 2
4	четверичная	0, 1, 2, 3
5	пятеричная	0, 1, 2, 3, 4
8	восьмеричная	0, 1, 2, 3, 4, 5, 6, 7
10	десятичная	0, 1, 2, 3, 4, 5, 6, 7, 8, 9
12	двенадцатиричная	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B
16	шестнадцатеричная	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

В общем случае в позиционной системе счисления по некоторому основанию число

X=a_n–1 a_n–2… a₁ a₀ a_–1 a_–2 …a_–m

можно считать обозначением полинома

X=a_n–1b^n–1+ a_n–2b^n–2+…+ a₁b¹+ a₀b⁰+ a_–1b^–1…+a_–m b^–m.

В этой общей форме a_i – цифры, лежащие в диапазоне 0a_i<b; n и m – количество разрядов в целой и дробной частях числа соответственно; b – основание системы счисления; bⁱ – разрядный вес i-й цифры.

Запись числа в b-ичной системе счисления называют b-ичным кодом числа. Двоичный, восьмеричный и шестнадцатеричный коды десятичного числа, например, 19,375 выглядят следующим образом:

19,375₍₁₀₎=10011,011₍₂₎=23,3₍₈₎=13,6₍₁₆₎.

Десятичный индекс, сопровождающий число, указывает основание системы счисления. Индекс опускается, когда основание системы счисления известно из контекста.

В виде полиномов уже рассмотренное десятичное число 19,375 можно записать так:

19,375₍₁₀₎=10011,011₍₂₎=12⁴+02³+02²+12¹+12⁰+02^–1+12^–2+12^–3 =

=16+0+0+2+1+0+1/4+1/8.

19,375₍₁₀₎ =23,3₍₈₎=28¹+38⁰+38^–1=16+3+3/8.

19,375₍₁₀₎ =13,6₍₁₆₎=116¹+316⁰+616^–1=16+3+6/16.

Таблица 4.2 – Коды чисел в различных позиционных системах счисления

Десятичные	Двоичные	Восьмеричные	Шестнадцатеричные
0 1 2 3 4 5 6 7 8 9	00000 00001 00010 00011 00100 00101 00110 00111 01000 01001	0 1 2 3 4 5 6 7 10 11	0 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19	01010 01011 01100 01101 01110 01111 10000 10001 10010 10011	12 13 14 15 16 17 20 21 22 23	A B C D E F 10 11 12 13
20 21 22 23 24 25 26 27 28 29	10100 10101 10110 10111 11000 11001 11010 11011 11100 11101	24 25 26 27 30 31 32 33 34 35	14 15 16 17 18 19 1A 1B 1C 1D
30 31	11110 11111	36 37	1E 1F
32	100000	40	20

Числа, записанные в недесятичных системах счисления, следует произносить не так, как в десятичной системе. Например, восьмеричное число 23,3 рекомендуется читать так: "два–три–запятая–три" в отличие от привычного для нас чтения десятичного числа 23,3, а именно двадцать три целых и три десятых".

Для ЭВМ наилучшей системой счисления оказалась двоичная из-за простоты технической реализации, наибольшей помехоустойчивости кодирования цифр, минимума затрат оборудования, простоты арифметических действий, наибольшего быстродействия и возможности применения формального математического аппарата для синтеза и анализа вычислительных устройств. Десятичная система счисления удобнее для человека с точки зрения удобства работы, но сильно проигрывает двоич­ной по остальным требованиям. Оценим, например, затраты оборудова­ния для запоминания числа 5839 в десятичной системе. Нам потребу­ется четыре десятичных разряда по десять устойчивых состояний в каждом, то есть всего 40 устойчивых состояний. В двоичной системе счисления для этого же числа 5839, выраженного как 1 0110 1100 1111, достаточно иметь 13 разрядов на два устойчивых состояния в каждом – всего 26 устойчивых состояний, что примерно в 1,5 раза меньше.

Восьмеричная и шестнадцатеричная системы счисления в вычисли­тельной технике имеют вспомогательное значение. Запись чисел в этих системах получается более компактной и удобной для человека, чем в двоичной системе.

В машинах первого и второго поколений наибольшее распростране­ние получила восьмеричная система. Этому способствовало то, что в ней можно было пользоваться цифрами десятичной системы, не прибе­гая к каким-либо новым символам, что нельзя сделать при использо­вании шестнадцатеричной системы.

В машинах третьего и более поздних поколений вместо восьмеричной чаще стала использоваться шестнадцатеричная система, так как это унифицирует форматы числовой и командной информации и обеспечивает более корот­кие записи.

В ЭВМ третьего и более поздних поколений за основную единицу информации при­нят байт. Один байт равен 8 битам, то есть описывается восемью двоичными разрядами. В шестнадцатеричной системе для записи инфор­мации, содержащейся в одном байте, требуется 2 символа, а в вось­меричной – 3, причем старший разряд восьмеричного числа недоиспользуется.

Перевод целых чисел из одной позиционной системы в другую

Предположим, что число X уже переведено в новую систему счисления, тогда в позиционной системе счисления с основанием b оно может быть записано в виде

X=a_n–1b^n–1 + a_n–2b^n–2 +…+ a₁b + a₀.

Разделим левую и правую части этого выражения на основание b. Получим

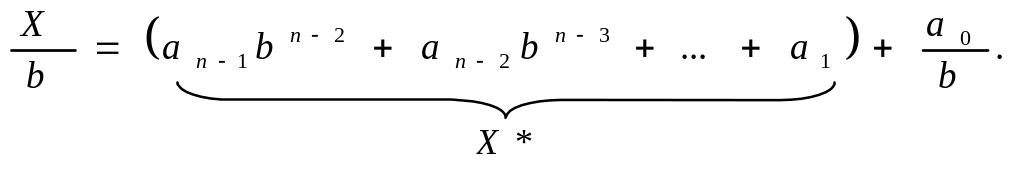
В этом выражении есть целая часть X*, заключенная в скобки, и первый остаток a₀.

Разделив целую часть X* на основание системы счисления b, получим второй остаток a₁. Повторяя процесс деления n раз, получим цифры числа, представленного в системе счисления с основанием b. Все операции необходимо выполнять в исходной системе счисления.

Пример 1. Перевести десятичное число 92 в двоичную систему счисления (b=2).

Решение.

Таким образом, 92₍₁₀₎=1011100₍₂₎. Проверка: 1011100₍₂₎=2⁶+2⁴+2³+2²=92­₍₁₀₎.

Пример 2. Переведем двоичное число Х=1011100 в десятичную систему счисления. Выразим основание новой системы счисления через исходную систему: b=10₍₁₀₎=1010₍₂₎.

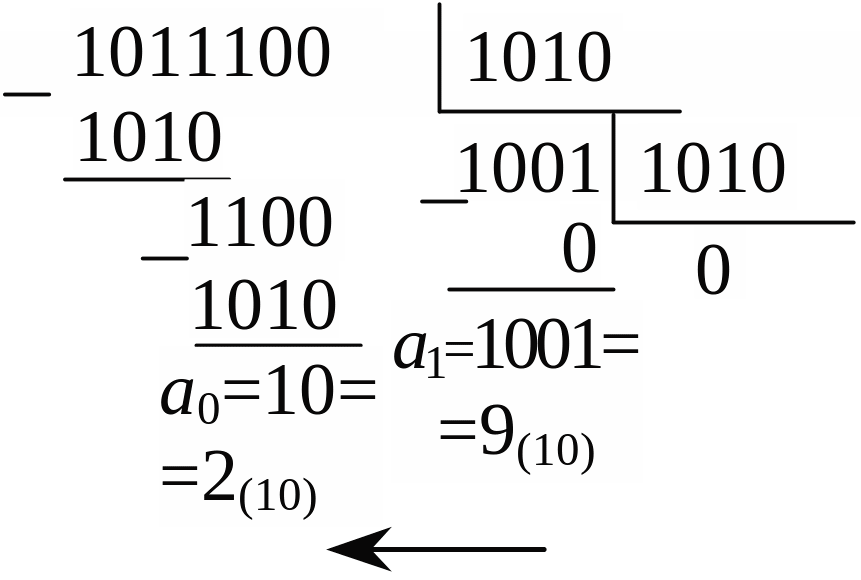
Это десятичное число 92.

Пример 3: Перевести двоичное число 11101011 в десятичное.

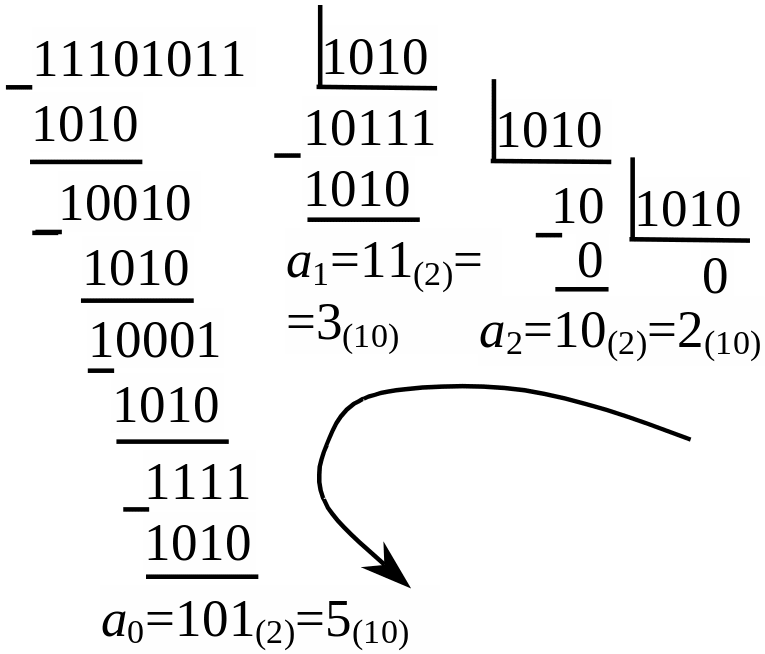
Получилось X=11101011₍₂₎ =235₍₁₀₎.

Пример 4. Перевести десятичное число Х=983 в восьмеричную систему счисления.

X=983₍₁₀₎=1727₍₈₎.

Пример 5. Перевести десятичное число 42936 в шестнадцатеричное число.

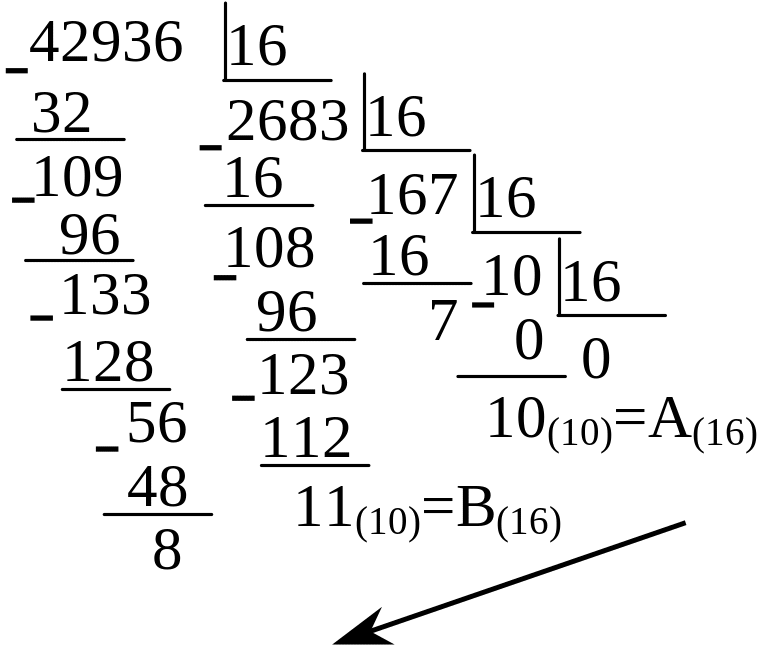
Ответ: 42936₍₁₀₎=A7B8₍₁₆₎.