Современные проблемы физики / PhysicalReviewpdf / Silagadze-1

1

З.К. Силагадзе.

Сколько ангелов может танцевать на булавочной головке?

24.10.2004

У вас вызывает улыбку этот вопрос? А было время подобные вопросы были предметом жарких споров среды вид-

ных схоластов. Один из них, Дунс Скот (1265-1308) увековечил свое имя даже в современном английском языке

(англ. "dunce" - "тупица")[1]. Если ваша улыбка от этого

расплылась еще больше, то зря. Дунс Скот отнюдь не был тупицей. В 1305 г. в Париже он даже защитил докторскую

диссертацию, в которой отстаивал (против доминиканцевтомистов) изначальную непорочность Пресвятой Девы Ма-

рии [2]. При этом, по легенде, мраморная статуя Богороди-

цы одобрительно кивала ему головою [2]. Но Легенды ле-

гендами, а исторически достоверно известно, что парижский факультет признал доводы Скота настолько убедительными, что тогда же постановил требовать впредь ото всех, ищущих ученой степени, клятвенного исповедания

веры в непорочное зачатие [2]. Не пора ли напомнить об

этом нашему ВАК-у?

Мне жаль вашей непорочной улыбки. Чтобы она сохранилась возможно дольше, я поместил здесь изображение прелестной скульптуры Джеймса Кристенсена [3] "How Many Angels Can Dance on the Head of a Pin?" (англ. "pin" имеет значение не только

"булавка", но и "кегля". По приведенной ссылке вы можете посмотреть и другие произведения этого замечательного мастера).

А ваша улыбка непременно пропадет после осознания того факта, что возникновение схоластики означает водораздел в истории христианства, водораздел который

прошелся по нашим с вами судьбам читатель!

Схоластикой называется возникшее на западе движение, посвященное исследованию роли человеческого разума в христианской вере. И возникло это движение в

эпоху "великого раскола", когда христианство официально разделилось на восточный и западный лагеря, известные сегодня как Православие и Католицизм [1].

В результате богословский подход стал более рациональным на Западе в противо-

положность более мистическому - на Востоке [1]. Чтобы ни говорили атеисты, особенности религиозных верований народа оставляют глубокую печать на его истории,

культуре и даже экономике. И глядя на сверкающее благополучие Запада, дьявол то и дело искушает усомниться в православном выборе наших предков. Мне кажется

ответ Николая Васильевича Гоголя на эти искушения полезен не только Русскому

народу, но и всем другим, которые хотят сохранить свою самобытность: "И прежде, и теперь, мне казалось, что русский гражданин должен знать дела Европы. Но я был

2

убежден всегда, что если при этой похвальной жадности знать чужеземное, упустишь из виду свои русские начала, то знания эти не принесут добра, собьют, спутают

и разбросают мысли, на место того чтобы сосредоточить и собрать их. И прежде, и теперь я был уверен в том, что нужно очень хорошо и очень глубоко узнать свою

русскую природу и что только с помощью этого знания можно почувствовать, что именно следует нам брать и заимствовать из Европы, которая сама этого не гово-

рит" [4].

Гоголь хорошо понимал, что на основе одной только догматической рациональности не ответишь на вопрос "Сколько ангелов может танцевать на булавочной головке?" так прекрасно, как это сделал художник Кристенсен. Останется одно лишь умнича-

ние и высмеивание схоластов подобно поздним гуманистам, по существу открывающее дорогу в ад. "Поразительно: в то время, когда уже было начали думать лю-

ди, что образованием выгнали злобу из мира, злоба другой дорогой, с другого конца входит в мир, - дорогой ума, и на крыльях журнальных листов, как всепогубляющая саранча, нападает на сердце людей повсюду. Уже и самого ума почти не слышно"

[5].

Хотя физика и считается венцом рациональности и далекой от восточного мисти-

цизма, ее ответ, если только его отыскать среди всепогубляющих современных журнальных листов, оказывается не менее занятным и поразительным, чем ответ искусства.

Во-первых, как это обычно делается в физике, предельно упростим ситуацию, оставляя только самое существенное. Что самое существенное в ангелах? Разумеется

ангельская информация, которую они несут. Каждый ангел несет по крайнее мере

один бит информации (падший, не падший) [6]. Таким образом приходим к следующей задаче: каково максимальное количество информации, которую может содержать устройство с размером булавочной головки? Таков современный вариант вопроса о танцующих ангелах. В такой постановке современная физика может предложит вполне интересную интерпретацию. Например, наподобие такой, которую приводит Якоб Бекенштейн (Jacob Bekenstein) в своей статье в Scientific American [7]. Для удобства читателя, ниже мы приводим (красным цветом) русский перевод этой статьи с некоторыми нашими комментариями.

Спросите любого из чего сделан физический мир вокруг нас и скорее всего получите

в ответ: "Из вещества и энергии". Тем не менее, если инженерная наука, биология и физика чему-либо и научили нас, это то, что информация тоже является такой же важной составляющей частью. Робот на автомобильном заводе, даже имея в достаточном количестве метал и пластик, не может произвести ничего полезного без многочисленных инструкций, например, какую часть чем приварить и так далее. Рибо-

сома в клетке вашего организма может иметь необходимые аминокислоты и достаточную энергию, высвобождающуюся при превращении АТФ в АДФ, но она не смо-

жет синтезировать белки без информации, которая предоставляется ей через ДНК в ядре клетки. Столетнее развитие физики тоже учит нас, что информация является ключевым игроком в физических системах и процессах. Действительно, современ-

ная тенденция, начало которой было положено Джоном Уилером из Принстонского Университета, состоит в том, чтобы считать физический мир состоящим из информации, которой случайно сопутствуют энергия и вещество.

В современной физике информация еще не стала центральным игроком, но может быть и станет, если квантовые компьютеры станут реальностью. В свое время Рене

3

Декарт дал краткое и емкое определение термину "существовать": "Мыслю - значит существую". Но что значит Мыслить? Это обработка информации. Поэтому не уди-

вительно, что Джон Арчибальд Уилер довел идею Декарта до логического конца: "бытие дается битом" ("it from bit") [8]. Имеется в виду, что вещь должна содержать

хотя бы один бит информации, который позволит ответить да или нет при проведении эксперимента над этой вещью, чтобы мы могли считать, что вещь существует.

Эта точка зрения предлагает по-новому взглянуть на старые вопросы. Информаци-

онная емкость устройств типа жесткого диска компьютера растет гигантскими шагами. Когда остановится этот прогресс? Какова максимальная информационная емкость устройства, который весит, скажем, меньше, чем грамм и занимает объем

меньше, чем кубический сантиметр (примерно размер компьютерной микросхемы). Сколько информации требуется, чтобы описать всю Вселенную? Уместится ли это

описание в память компьютера? Можем ли мы, как Уильям Блейк отчеканил свое время "увидеть вселенную в песчинке" или эта идея всего лишь поэтическая вольность?

Примечательно, что недавние результаты в теоретической физике отвечают на некоторые из этих вопросов, и

эти ответы могут оказаться важным ключом в поисках окончательной теории окружающей реальности. Изучая

таинственные свойства чёрных дыр, физики вывели абсо-

лютные пределы на то, сколько информации может содержать область пространства или некоторое количество вещества и энергии. Связанные с этим результаты указывают, что наша Вселенная, которую мы воспринимаем как

имеющую три пространственных измерения, на самом де-

ле может быть "написана" на двухмерной поверхности, подобно голограмме. Наше повседневное восприятие мира как трёхмерного тогда

было бы или основательно запутанной иллюзией, или просто одним из двух альтернативных путей рассмотрения реальности. Песчинка, видимо, не может охватить наш мир, но плоский экран мог бы.

Двадцатый век знаменует три революционные физические теории, которые измени-

ли наши представления о мире и о том, что значит "существовать": специальная теория относительности, квантовая механика и общая теория относительности. Специальная теория относительности на вопрос 19-го столетия "Что электродинамика нам говорит о природе реальности?" дал простой, но парадоксальный для своего времени ответ: "Поля в пустом пространстве обладают физической реальностью, а среда, которая бы поддерживала эти поля - нет" [9]. Общая теория относительности и квантовая механика еще должны найти общий язык, чтобы предложить

нам свою версию картины реальности. Некоторые думают, что теория суперструн и есть этот общий язык. Но пока этот "язык" страшно далёк от реальной жизни. Для

нас сейчас важно, что эта теория модифицирует общую теорию относительности, но не покушается на принципы квантовой механики. А квантовая механика предлагает самую загадочную картину мира, которую только мог представить себе физик 19-го

столетия. Развитием Уилеровской концепции бита, как мерила бытия является еще более радикальный ответ на вопрос "Что нам квантовая механика говорит о природе реальности?": "Корреляции обладают физической реальностью, а то, что они корре-

лируют - нет" [9]. Если вам эта точка зрения кажется слишком уж странной, могу ус-

покоить - она не является общепринятой и вы можете не сомневаться в своем собственном существовании (пока). Но чтобы продемонстрировать, насколько странен

4

квантовомеханический взгляд на мир, рассмотрим так называемый мысленный экс-

перимент Уилера с отложенным выбором [10], [11].

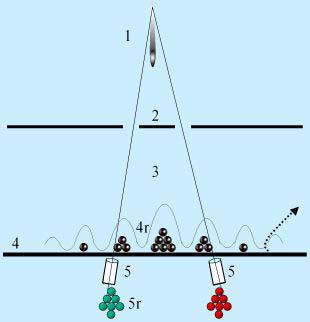
Источник 1 испускает по одному фотону по команде экспериментатора. На пути фотона расположен двух-щелевой экран 2 а даль-

ше фотоэмульсия 4, которая регистрирует место попадания фотона. Как известно, по-

сле записи множества таких событий, на фотоэмульсии появится интерференционная картина 4r - фотон проявит свою вол-

новую природу, проходя одновременно через обе щели. Но фотоэмульсия скрывает

другой измерительный прибор - пару плотно коллимированных телескопов 5 с камерами фотоумножителей, чувствительными к

единичным фотонам и расположенными в фокусе телескопов, каждый из которых на-

веден на свою щель. Если фотоэмульсию убрать, будет совсем другой эксперимент -

фотон проявит свою корпускулярную природу, пройдя или через одну, или через другую щель, что надежно зафиксируют наши телескопы с фотоумножителями. Дуализм волна-частица, скажете вы. Конечно странно, но привыкли за долгую историю квантовой механики. Но здесь появляется

Уилер, как фокусник, и показывает, что это наше представление о дуализме волна-

частица никуда не годится. Он рассуждает так: экспериментатору известно, сколько времени требуется фотону, чтобы долететь до щели. Давайте подождем это время. Еще какой-то промежуток времени фотон летит к фотоэмульсии. В течение этого времени мы можем спокойно решить, какой эксперимент провести, то есть быстро

убрать фотоэмульсию или нет. Выходит, "решение" фотона проявить свою волновую

или корпускулярную природу при прохождении щели зависит от нашего решения, которое мы принимаем когда фотон давно уже миновал щели! Нет никакого дуализма волна-частица. Есть квантовая механика, которая раскрывает природу реальности, которая более странная, чем мы могли представить. Не зря говорил Гелл-Манн:

"Квантовая механика, эта таинственная, приводящая в замешательство дисциплина,

которую никто из нас по-настоящему не понимает, но которую мы знаем как использовать".

Подобные эксперименты с отложенным выбором действительно были проведены и, конечно, подтвердили квантовую механику. Есть даже совсем поражающий вообра-

жение эксперимент, когда решение экспериментатора откладывается до момента пока квант не достигнет фотоэмульсии. А потом информацию о том, прошел он через обе щели или через одну из них, по желанию можно "стирать" используя другой

квант, квантово-механически запутанный с первым [12]. Сам Уилер, исследуя физический и философский подтекст похожих экспериментов, пришел к часто цитируемой

парадигме: "Ни один феномен не является феноменом до тех пор, пока это не наблюдаемый феномен.[11]" Вот такой экстравагантный ответ на вопрос Эйнштейна

"существует ли Луна, если никто на нее не смотрит?" [13].

5

Рассказ о двух энтропиях

Формальная теория информации началась с ключевой работы 1948 года Американского прикладного математика Клода Шеннона, который ввел ныне самую распространенную меру информационного содержания: энтропию. Энтропия до этого давно была центральной концепцией термодинамики, раздела физики, который изучает тепловые явления. Термодинамическая энтропия популярно понимается как мера беспорядка в физической системе. В 1877 г. Австрийский физик Людвиг Больцман дал более точное определение термодинамической энтропии через число разных микроскопических состояний частиц, составляющих кусок вещества, при которых этот кусок всё ещё выглядит как один и тот же макроскопический кусок вещества. Например, для воздуха в комнате вокруг вас, надо посчитать, сколькими способами могут быть распределены индивидуальные молекулы газа в комнате и всевозможные пути их движения.

Когда Шеннон рассматривал вопрос, каким образом количественно измерять ин-

формацию, которая содержится, скажем, в сообщении, логика привела его к формуле такого же вида, как у Больцмана. Энтропия Шеннона для сообщения равна числу

двоичных знаков, или битов, нужных для кодировки этого сообщения. Энтропия Шеннона ничего не говорит нам о качестве информации, которое сильно зависит от содержания. Тем не менее, как объективная мера количества информации, она

весьма полезна в науке и технике. Например, разработка каждого современного средства коммуникации, от сотовых телефонов до модемов и до проигрывателей компакт-дисков, не обходится без энтропии Шеннона.

Термодинамическая энтропия и энтропия Шеннона концептуально эквивалентны:

число разных комбинаций в энтропии Больцмана отражает количество информации

Шеннона, которое бы понадобилась для обеспечения возможности осуществить любую из этих комбинаций. Однако, эти две энтропии имеют два важных различия. Вопервых, термодинамическая энтропия, используемая химиком или инженером холодильной техники, выражается в единицах энергии, делённой на температуру, тогда

как энтропия Шеннона, используемая инженером коммуникационных сетей, выража-

ясь в битах, по существу безразмерна. Это различие - всего лишь дело соглашения.

Даже выраженные в одинаковых единицах, типичные значения двух энтропий отличаются многократно по величине. Кремниевая микросхема, несущая гигабайт данных, например, имеет Энтропию Шеннона порядка 1010 бит (один байт равен восьми битам). Это во много раз меньше термодинамической энтропии микросхемы, кото-

рая примерно равна 1023 бит при комнатной температуре. Это различие возникает

потому, что две энтропии вычисляются для разных степеней свободы. Степень свободы - это любая величина, которая может изменяться, подобно координате, харак-

теризующей положение частицы, или одной из компонент ее скорости. Для энтропии Шеннона важно только общее состояние каждого миниатюрного транзистора, вы-

травленного в кремниевом кристалле. Транзистор или открыт или нет, что соответствует или 1 или 0 - простая двоичная степень свободы. Термодинамическая энтропия, наоборот, зависит от состояний всех миллиардов атомов (и электронов паря-

щих около них), составляющих каждый из транзисторов. Миниатюризация приближает день, когда каждый атом будет хранить один бит информации для нас. В такой

воображаемой микросхеме энтропия Шеннона приблизится по величине к термодинамической энтропии материала микросхемы. Когда две энтропии вычислены для

одинаковых степеней свободы, они совпадают.

Каковы самые первичные степени свободы? Атомы, в конце концов, сделаны из электронов и ядер. Ядра представляют собой конгломерат протонов и нейтронов и

эти последние в свою очередь состоят из кварков. Сегодня многие физики рассмат-

6

ривают электроны и кварки как возбуждения суперструн, которые они гипотетически принимают за самые фундаментальные сущности. Но превратности последнего сто-

летия неожиданных открытий в физике учит нас не быть догматиками. Может быть в нашей Вселенной уровней структуры больше, чем можно представить в современ-

ной физике.

Нельзя вычислить максимальную информационную емкость некоторого количества вещества, или, что эквивалентно, его настоящую термодинамическую энтропию, без

знания природы самых фундаментальных составляющих материи или самого глубокого уровня структуры, который я назову уровнем X. Это незнание не создает проблем для практической термодинамики, например, автомобильных двигателей, так

как при этом кварки внутри атомов могут быть игнорированы - они не меняют своего состояния под действием сравнительно мягких условий в двигателе. Но, наблюдая

удивительный прогресс в миниатюризации, можно играючи представить день, когда кварки будут использованы для хранения информации, возможно, один бит на кварк. Сколько информации можно тогда вместить в наш одно-сантиметровый куб? И

сколько, если мы обуздаем суперструны или даже более глубокий, пока еще невообразимый уровень? Как ни удивительно, результаты развития физики гравитации за

последнее три десятилетия предоставляют некоторые ясные ответы на эти казалось бы сумбурные вопросы.

Говорят, что использовать термин "энтропия" советовал Шеннону фон Нейман, до-

бавляя при этом: "это даст вам большое преимущество в спорах, так как никто на самом деле толком не знает, что же такое энтропия" [14]. Слова Неймана подтверждается тем фактом, что Ч.П.Сноу получил весьма холодную и отрицательную реакцию своих коллег, когда он в 1959 г. в своей Ридовской лекции в Кембридже провоз-

гласил, что незнание второго начала равносильно незнакомству с Шекспиром. Зря

он не внял советам: ведь еще в 1873 году ридовского лектора предупреждали "не говорить о втором начале термодинамики как о чем-то давно известном культурным людям, которые не слышали даже о первом начале" [15].

Клод Шеннон мог бы стать мультимиллиардером, так как вся современная индустрия цифровой передачи данных основана на его идеях. Но он умер 1 марта 2001 го-

да в массачусетском доме для престарелых, забытый почти всеми. В сакраменталь-

ном вопросе "Иметь или быть" [16], ему было судьбой предначертано быть гениальным и эксцентричным человеком. Шеннон неоднократно отмечал, что мотивацией

его деятельности в значительно большей степени было любопытство, чем практиче-

ская выгода: "Я всегда следовал своим интересам, не думая ни о том, во что они для

меня выльются, ни об их ценности для мира. Я потратил уйму времени на совершенно бесполезные вещи... Мне просто было интересно, как эти вещи устроены".

Временами Шеннон любил разъезжать по коридорам Bell Labs на одноколесном велосипеде, да еще жонглируя при этом мячами. А после ухода в 1978 году на пенсию ученый полностью отдался своей давней страсти - жонглированию. Шенноном было

построено несколько жонглирующих машин и даже была создана "общая теория жонглирования" [17].

Если вам все-таки захотелось глубже понять связь между физикой и информацией, можно посоветовать не очень техническую статью [18].

7

Термодинамика чёрных дыр

Чёрная дыра играет роль центрального игрока в этих исследованиях. Существование чёрных дыр есть следствие общей теории относительности, геометрической теории гравитации, созданной Альбертом Эйнштейном в 1915 г. В этой теории гравитация есть следствие искривления пространствавремени, которое заставляет предметы двигаться, как если бы их тянула сила притяжения. И наоборот, искривление пространства-времени вызывается присутствием материи и энергии. Согласно уравнениям Эйнштейна, достаточно большая концентрация вещества или энергии так сильно искривляет пространство-время, что оно замыкается, образуя чёрную дыру. Законы общей теории относительности запрещают вещам, упавшим в чёрную дыру, вернуться обратно. По крайнее мере, так выглядят дела, если пренебрегать квантовыми свойствами материи. Точка невозврата (точнее - поверхность в пространстве-времени - ред. ), так называемый "горизонт событий" черной дыры, имеет ключевое значение. В простейшем случае горизонт событий черной дыры представляет собой сферу, поверхность которой больше для более массивной черной дыры.

Невозможно определить, что происходит внутри черной дыры. Никакая детальная

информация не может выйти из-под горизонта событий и вырваться во внешний мир. Исчезая навсегда в черной дыре, кусочек вещества, однако, оставляет некоторые следы. Его энергия (а каждую массу можно рассмотреть как энергию согласно

формуле Эйнштейна E=mc2) проявляет себя во возрастании массы черной дыры. Если кусочек вещества поглощается с орбиты, то соответствующий момент импульса добавляется к моменту импульса черной дыры. Как масса, так и момент черной дыры измеримы по их влиянию на окружающее черную дыру пространство-время. В этом смысле законы сохранения энергии и момента импульса не нарушаются черными дырами. Другой фундаментальный закон, второй закон термодинамики, наоборот, кажется нарушенным.

Второй закон термодинамики обобщает обычные наблюдения, что большинство процессов в природе не обратимо: чайная чашка падает со стола и разбивается, но

никто никогда не наблюдал, чтобы осколки сами притянулись на стол и снова объе-

динились в чайную чашку. Второй закон термодинамики запрещает такой обратный процесс. Он говорит, что энтропия изолированной физической системы никогда не

уменьшается. Самое большее - энтропия не будет меняться, а обычно она растет.

Этот закон является центральным в физической химии и в инженерном деле. Можно утверждать, что он является физическим законом с наибольшим влиянием вне физики.

Как впервые подчеркнул Уилер, когда вещество исчезает в черной дыре, ее энтропия пропадает навсегда, и, сле-

довательно, второй закон термодинамики как бы наруша-

ется. Ключ к разгадке этой загадки появился в 1970 г., ко-

гда Деметриос Христодулу (Demetrious Christodoulou), в то время аспирант Уилера в Принстоне, и Стивен Хокинг в

Кембридже независимо друг от друга обнаружили, что в различных явлениях, таких как, например, слияние двух

черных дыр, суммарная площадь горизонта событий никогда не уменьшается. Аналогия с законом возрастания эн-

тропии подсказала мне в 1972 г. идею, что черная дыра имеет энтропию, пропор-

циональную площади поверхности ее горизонта событии. Моя гипотеза состояла в том, что когда материя падает в черную дыру, увеличение энтропии черной дыры всегда компенсирует или превосходит по величине "потерянную" энтропию материи. Более обобщённо, сумма энтропии черных дыр и обычной энтропии вне черных дыр никогда не уменьшается. Это и есть обобщённый второй закон - ОВЗ, для краткости.

9

Если масса может коллапсировать в черную дыру, у этой дыры площадь горизонта будет меньше, чем A. Эн-

тропия черной дыры, следовательно, не превосходит величину A/4. Но согласно ОВЗ, энтропия системы не мо-

жет уменьшаться. Следовательно, первоначальная энтропия исходной массы была не больше A/4. Как видим, энтропия изолированной физической системы с поверх-

ностью A не превышает A/4. Но что если масса не коллапсирует спонтанно? В 2000 г. я показал, что можно ис-

пользовать маленькую черную дыру, чтобы превратить исходную систему масс в черную дыру почти такую, которую использовал Сасскинд в своих рассуждениях. (Такой мысленный процесс с

использованием маленькой черной дыры предложил Я.Б.Зельдович лет на 40 раньше для того, чтобы показать метастабильность любой системы масс относительно

коллапса - ред..) Энтропийный предел, следовательно, не зависит от общего устройства системы и от природы уровня X. Он зависит только от справедливости ОВЗ.

Теперь мы можем ответить на те ускользающие вопросы о максимальном количест-

ве хранимой информации. Устройство, имеющее 1см размер, в принципе может хранить до 1066 бит информации - умопомрачительная величина. Видимая Вселен-

ная содержит по крайнее мере 10100 бит энтропии, которую в принципе можно поместить в сфере радиусом в одну десятую светового года. Однако оценить энтропию Вселенной сложно, и значения энтропии гораздо большие, требующие для упаковки сферы почти такого же размера, как сама Вселенная, со-

всем не исключены.

Но совсем другой аспект голографического предела явля-

ется действительно удивительным. В частности, максимальное количество энтропии зависит от окружающей поверхности, а не от объема. Представим, что мы собираем

микросхемы памяти компьютера в большую кучу. Число транзисторов и, следова-

тельно, информационная емкость растут с объемом кучи. То же самое происходит с

полной термодинамической энтропией всех микросхем. Однако теоретическая максимальная информационная емкость области пространства, занятой микросхемами, растет, заметьте, только с увеличением поверхности. Так как объем растет быстрее, чем площадь поверхности, наступит момент, когда энтропия всех микросхем превы-

сит голографический предел. Кажется, тогда или ОВЗ должен нарушиться или наши

представления об информационной и энтропийной ёмкости окажутся неправильны-

ми. На самом деле, фиаско терпит само собрание микросхем: под действием собственной гравитации оно коллапсирует и превращается в черную дыру до того, как го-

лографический предел будет превзойден. После этого каждая дополнительная микросхема будет увеличивать массу и площадь поверхности черной дыры в полном согласии с ОВЗ.

Этот удивительный результат - что информационная емкость зависит от площади поверхности - находит естественное объяснение, если голографический принцип,

предложенный в 1993 г. Нобелевским лауреатом Герардом Хоофтом из Нидерландов и развитый дальше Сасскиндом, соответствует истине. В обычной жизни голограмма представляет специальную разновидность фотографии, при которой воссоз-

дается полный трехмерный образ предмета при специальном освещении. Вся ин-

формация, описывающая трехмерную картину, закодирована в виде темных и светлых полос на двумерной пленке, готовой к воспроизведению. Голографический

10

принцип утверждает, что некоторый аналог этой оптической магии применим для полного физического описания любой системы в трехмерной области: он утвержда-

ет, что другая физическая теория, определенная только на двумерной поверхности, ограничивающей данную область, полностью описывает трехмерную физику внутри

области. Если трехмерная система полностью может быть описана некоторой физической теорией, обитающей целиком на двумерной границе области, то мы вправе ожидать, что информационное содержание системы не будет превышать соответст-

вующее описание на граничной поверхности.

Как вы думаете, что изображено на этой двумерной картине? Если ваша работа связана компьютером и требует непрерывного напряжения глаз, то самое время дать

глазным мышцам расслабиться путем переключения на более удаленные планы. Представьте себе, что вы рассматривайте не пеструю плоскую панораму на экране

монитора, а некий объект, спрятанный за экраном на расстоянии сантиметров этак 15-20. Если вам удастся так расфокусировать ваше зрение, произойдет чудо и вы увидите двух кроликов, причем во всем трехмерном великолепии. Подобные стерео-

граммы впервые создал в 1989 году Кристофер Тайлер, используя результаты известного психолога Белы Юлеша [22].

Наряду с голограммами, стереограммы тоже хорошие метафоры голографического

принципа. Но при этом опять поднимается вопрос об соотношении реальности и

сознания. Ведь трехмерную картину кроликов конструирует наш мозг! Мы не будем здесь дальше развивать эту сложную и запутанную тему. Любителям нестандартных и интересных мыслей укажем на книгу Фритьофа Капра "Точка поворота" [23].

Вселенная, нарисованная на своей границе

Можем ли мы применить голографический принцип ко всей Вселенной? Реальная Вселенная является 4-мерной системой: она имеет объем и временное протяжение. Если физика нашей Вселенной голографическая, тогда должно существовать альтернативное множество физических законов, действующих где-нибудь на трехмерной границе пространства-времени и полностью определяющих нашу привычную 4-мерную физику. Мы пока не знаем ни одной трехмерной теории, которая работает подобным образом. На самом деле, какую поверхность мы должны использовать как границу Вселенной? Первый шаг к реализации подобных идей состоит в рассмотрении моделей, которые проще, чем наша реальная Вселенная.