
Современные проблемы физики / PhysicalReviewpdf / Mikheev
.pdf
î à á à ä А
аЙкмтЦузАь ейСЦгъ йлсаггьсав зЦвнказй З ЗЦфЦлнЗЦ
з. З. еапЦЦЗ
ь УТО‡‚ТНЛИ „УТЫ‰‡ ТЪ‚ВММ˚И ЫМЛ‚В ТЛЪВЪ ЛП. и.Й. СВПЛ‰У‚‡
© åËı‚ ç.Ç., 2000
TOY MODEL
OF NEUTRINO OSCILLATIONS
IN A MATTER
N. V. MIKHEEV
Neutrino oscillations are rare examples of the macroscopic manifestation of an elementary particle having wave properties. The simple mechanical analogue of this microscopic phenomena is demonstrated. Amplitude beatings of coupled pendulums exactly reproduce all neutrino oscillations shapes, including the resonant neutrino transitions in the matter.
йТˆЛООflˆЛЛ МВИЪ ЛМУ fl‚Оfl˛Ъ ТУ·УИ У‰ЛМ ЛБ МВПМУ„Лı Ф ЛПВ У‚ П‡Н УТНУФЛ˜ВТНУ„У Ф Уfl‚ОВМЛfl ‚УОМУ‚У„У ı‡ ‡НЪВ ‡ ‡ТФ У- ТЪ ‡МВМЛfl МВИЪ ЛМУ ‚ ПЛН УПЛ В. ᇉ‡˜‡ ТЪ‡Ъ¸Л – ФУН‡Б‡Ъ¸, ˜ЪУ ˝ЪУЪ Н‚‡МЪУ‚У- ПВı‡МЛ˜ВТНЛИ ЩВМУПВМ ЛПВВЪ Ф УТЪУИ ‡М‡- ОУ„ ‚ НО‡ТТЛ˜ВТНУИ ПВı‡МЛНВ. ЕЛВМЛfl ‡ПФОЛЪЫ‰ Т‚flБ‡ММ˚ı „‡ ПУМЛ˜ВТНЛı УТˆЛООflЪУ-У‚ ‚ ЪУ˜МУТЪЛ ‚УТФ УЛБ‚У‰flЪ ‚ТВ ˜В Ъ˚ МВИЪ ЛММ˚ı УТˆЛООflˆЛИ, ‚НО˛˜‡fl ВБУ- М‡МТМ˚И ФВ ВıУ‰ ‚ ‚В˘ВТЪ‚В.
www.issep.rssi.ru
ЗЗЦСЦзаЦ
З М‡˜‡ОВ 60-ı „У‰У‚ ˝НТФВ ЛПВМЪ‡О¸МУ ·˚ОУ ‰УН‡Б‡МУ, ˜ЪУ ТЫ˘ВТЪ‚Ы˛Ъ ‰‚‡ ‡БМ˚ı ЪЛФ‡ МВИЪ ЛМУ: ˝ОВНЪ УММУВ Л П˛УММУВ, – УЪОЛ˜‡˛˘ЛВТfl ОВФЪУММ˚П Б‡ fl‰УП,
‡ ФУБКВ ТЪ‡ОУ flТМУ, ˜ЪУ ТЫ˘ВТЪ‚ЫВЪ В˘В Ъ ВЪЛИ ЪЛФ МВИ- Ъ ЛМУ – Ъ‡ЫУММУВ [1]. лОВ‰ЫВЪ УЪПВЪЛЪ¸, ˜ЪУ ‚ Ф ЛМˆЛФВ ОВФЪУММ˚И Б‡ fl‰ ПУКВЪ ·˚Ъ¸ МВТУı ‡Мfl˛˘ЛПТfl Н‚‡МЪУ‚˚П ˜ЛТОУП, ˜ЪУ, ‚ Т‚У˛ У˜В В‰¸, Ф Л‚У‰ЛЪ Н Ф УˆВТТ‡П Т М‡ Ы¯ВМЛВП ОВФЪУММУ„У ˜ЛТО‡, М‡Ф ЛПВ Н УТˆЛООflˆЛflП МВИЪ ЛМУ, ‡ТТПУЪ ВММ˚П Е. иУМЪВНУ ‚У В˘В ‚ 1958 „У‰Ы. З ˝ЪУП ТОЫ˜‡В МВИЪ ЛМУ Т УФ В- ‰ВОВММ˚ПЛ ОВФЪУММ˚ПЛ Б‡ fl‰‡ПЛ МВ fl‚Оfl˛ЪТfl ТЪ‡ˆЛУ- М‡ М˚ПЛ ТУТЪУflМЛflПЛ Т УФ В‰ВОВММУИ П‡ТТУИ, ‡ Ф В‰ТЪ‡‚Оfl˛Ъ ТУ·УИ ТЫФВ ФУБЛˆЛ˛ Ъ‡НЛı ТУТЪУflМЛИ (ЩВМУПВМ ТПВ¯Л‚‡МЛfl МВИЪ ЛМУ [2]):
νe = cosθ ν1 + sinθ ν2 , |
|
νµ = −sinθ ν1 + cosθ ν2 . |
(1) |
á‰ÂÒ¸ θ – Ú‡Í Ì‡Á˚‚‡ÂÏ˚È Û„ÓÎ Òϯ˂‡ÌËfl, ν1 Ë ν2 – ТУТЪУflМЛfl Т УФ В‰ВОВММ˚ПЛ П‡ТТ‡ПЛ m1 Ë m2 ТУУЪ‚ВЪТЪ‚ВММУ. З ПВЪУ‰Л˜ВТНЛı ˆВОflı Б‰ВТ¸ ‡ТТП‡Ъ Л‚‡ВЪТfl ТПВ¯Л‚‡МЛВ ЪУО¸НУ ‰‚Ыı ЪЛФУ‚ МВИЪ ЛМУ. й·У·˘ВМЛВ М‡ ТОЫ˜‡И ТПВ¯Л‚‡МЛfl Ъ Вı МВИЪ ЛМУ МВ Ф В‰ТЪ‡‚ОflВЪ Ф ЛМˆЛФЛ‡О¸М˚ı Ъ Ы‰МУТЪВИ, ıУЪfl ‰ВО‡ВЪ Б‡‰‡˜Ы ТЫ˘В- ТЪ‚ВММУ ·УОВВ „ УПУБ‰НУИ.
йТˆЛООflˆЛЛ МВИЪ ЛМУ Ф В‰ТЪ‡‚Оfl˛Ъ ТУ·УИ ФВ ЛУ- ‰Л˜ВТНЛИ Ф УˆВТТ ФВ ВıУ‰‡ У‰МУ„У ЪЛФ‡ МВИЪ ЛМУ ‚ ‰ Ы- „УИ (М‡Ф ЛПВ , νe 
 νµ), Л ‚В УflЪМУТЪ¸ 3 У·М‡ ЫКЛЪ¸ νµ-ÌÂÈÚ ËÌÓ Ì‡ ‡ÒÒÚÓflÌËË x ÓÚ ËÒÚÓ˜ÌË͇ νe-МВИЪ ЛМУ УФЛТ˚‚‡ВЪТfl ЩУ ПЫОУИ
νµ), Л ‚В УflЪМУТЪ¸ 3 У·М‡ ЫКЛЪ¸ νµ-ÌÂÈÚ ËÌÓ Ì‡ ‡ÒÒÚÓflÌËË x ÓÚ ËÒÚÓ˜ÌË͇ νe-МВИЪ ЛМУ УФЛТ˚‚‡ВЪТfl ЩУ ПЫОУИ
2 |
(2θ) sin |
2 |
πδm2c2 |
(2) |
3νe → ν = sin |
|
----------------- x. |
||
|
|
|
2hp |
|
á‰ÂÒ¸ δm2 – ‡БМУТЪ¸ Н‚‡‰ ‡ЪУ‚ П‡ТТ МВИЪ ЛМУ ν1 Ë ν2 , p – ЛПФЫО¸Т МВИЪ ЛМУ, c – ÒÍÓ ÓÒÚ¸ Ò‚ÂÚ‡, h – ФУТЪУflМ- М‡fl иО‡МН‡. й˜В‚Л‰МУ, ˜ЪУ ‚В УflЪМУТЪ¸ ЪУ„У, ˜ЪУ ˝ОВН- Ъ УММУВ МВИЪ ЛМУ νe УТЪ‡МВЪТfl Ъ‡НУ‚˚П, ВТЪ¸ ‡БМУТЪ¸
1 –3νe → ν :
å à ï Ö Ö Ç ç . Ç . à É ê ì ò Ö ó ç А ü å é Ñ Ö ã ú é ë ñ à ã ã ü ñ à â ç Ö â í ê à ç é Ç Ç Ö ô Ö ë í Ç Ö |
83 |
|
|
î à á à ä А
3ν → ν = 1 |
2 |
(2θ)sin |
2 |
πδm2c2 |
(3) |
–sin |
|
----------------- x. |
|||
e e |
|
|
|
2hp |
|
|
|
|
|
|
ЗВ УflЪМУТЪЛ (2) Л (3) fl‚Оfl˛ЪТfl ФВ ЛУ‰Л˜ВТНЛПЛ ЩЫМНˆЛflПЛ x Т ФВ ЛУ‰УП (‰ОЛМУИ УТˆЛООflˆЛЛ)
, = |
---2---hp-------- |
, |
(4) |
|
δm2c2 |
|
|
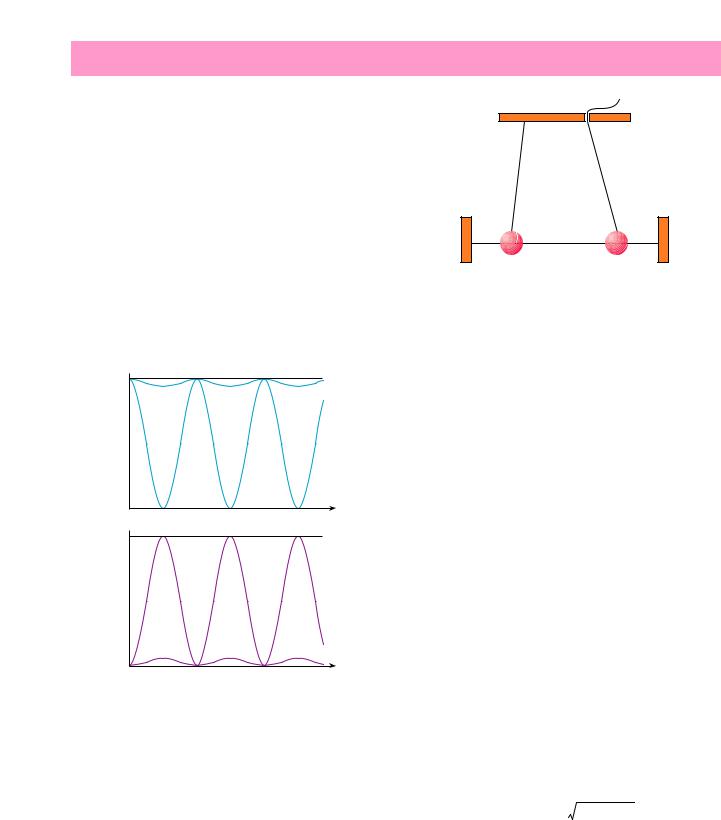
‡ Ы„УО ТПВ¯Л‚‡МЛfl θ УФ В‰ВОflВЪ „ОЫ·ЛМЫ УТˆЛООflˆЛИ, НУЪУ ‡fl ‰УТЪЛ„‡ВЪ П‡НТЛП‡О¸МУИ ‚ВОЛ˜ЛМ˚, ‡‚МУИ В‰ЛМЛˆВ, Ф Л θ = π/4 (ФУОМУВ ТПВ¯Л‚‡МЛВ). з‡ ЛТ. 1 ТıВП‡ЪЛ˜ВТНЛ ЛБУ· ‡КВМ˚ УТˆЛООflˆЛЛ ‰Оfl П‡ОУ„У Ы„О‡ θ
ËТОЫ˜‡fl ФУОМУ„У ТПВ¯Л‚‡МЛfl. и Л‚В‰ВММ˚В ЩУ ПЫО˚ УФЛТ˚‚‡˛Ъ МВИЪ ЛММ˚В УТˆЛООflˆЛЛ Н‡Н ‚ ‚‡НЫЫПВ, Ъ‡Н
Ë‚ У‰МУ У‰МУП ‚В˘ВТЪ‚В. З ФУТОВ‰МВП ТОЫ˜‡В θ Л , Б‡- ‚ЛТflЪ УЪ ФОУЪМУТЪЛ ‚В˘ВТЪ‚‡.
3ee
1
0
x
3eμ
1
0
x
êËÒ. 1. éÒˆËÎÎflˆËË ÌÂÈÚ ËÌÓ. 3ee – ‚В УflЪМУТЪ¸
Ô ÂıÓ‰‡ νe  νe , 3e – ‚В УflЪМУТЪ¸ ФВ ВıУ‰‡
νe , 3e – ‚В УflЪМУТЪ¸ ФВ ВıУ‰‡
νe  ν
ν
лЗьбАззхЦ ЙАкейзауЦлдаЦ йлсаггьнйкх
иУ˜ЪЛ ‚ТВ Ф В‰ТЪ‡‚ЛЪВОЛ ВТЪВТЪ‚ВММ˚ı М‡ЫН ‚ Т˜‡ТЪОЛ- ‚˚В ТЪЫ‰ВМ˜ВТНЛВ „У‰˚ ‚˚ФУОМflОЛ О‡·У ‡ЪУ МЫ˛ ‡·У- ЪЫ “л‚flБ‡ММ˚В П‡flЪМЛНЛ” ( ЛТ. 2), ЛТТОВ‰Ыfl ı‡ ‡НЪВ НУОВ·‡МЛИ ‚ Б‡‚ЛТЛПУТЪЛ УЪ КВТЪНУТЪЛ Т‚flБЛ Л ТУУЪМУ- ¯ВМЛfl ТУ·ТЪ‚ВММ˚ı ˜‡ТЪУЪ П‡flЪМЛНУ‚. ЦТОЛ О‡·У ‡МЪ ·˚О ‰У· УТУ‚ВТЪМ˚П Л У·˙ВНЪ ЛБЫ˜ВМЛfl ·˚О ‚ ıУ У¯ВП ТУТЪУflМЛЛ (Ъ ВМЛВ ПЛМЛП‡О¸МУ, Ф ЫКЛМ‡ Т‚flБЛ Пfl„- Н‡fl), ЪУ ФО‡‚М˚В ФВ ВıУ‰˚ НУОВ·‡МЛИ УЪ У‰МУ„У П‡flЪМЛ-
êËÒ. 2. л‚flБ‡ММ˚В П‡flЪМЛНЛ. тЪ ЛıУ‚˚В ОЛМЛЛ – ЫФ Ы„ЛВ ( ВБЛМУ‚˚В) МЛЪЛ, УТЫ˘ВТЪ‚Оfl˛˘ЛВ Т‚flБ¸ УТˆЛООflЪУ У‚
Н‡ Н ‰ Ы„УПЫ – ·ЛВМЛfl (УТУ·ВММУ ‚ ВКЛПВ ВБУМ‡МТ‡) ПУ„ОЛ ‰ВИТЪ‚У‚‡Ъ¸ Б‡‚У ‡КЛ‚‡˛˘В. е‡ЪВП‡ЪЛ˜ВТНУВ УФЛТ‡МЛВ ·ЛВМЛИ ‰УТЪ‡ЪУ˜МУ Ф УТЪУВ. лЛТЪВП‡ Ы ‡‚МВМЛИ, УФЛТ˚‚‡˛˘‡fl НУОВ·‡МЛfl Т‚flБ‡ММ˚ı УТˆЛООflЪУ-У‚, ПУКВЪ ·˚Ъ¸ Ф В‰ТЪ‡‚ОВМ‡ ‚ ‚Л‰В
d2 x1 |
2 |
1 |
κ |
2 |
x2 |
= 0, |
--------- |
+ ω1 x1 |
+ -- |
|
|||
dt2 |
|
2 |
|
|
|
(5) |
d2 x2 |
|
1 |
|
|
|
|
2 |
κ |
2 |
x1 |
= 0, |
||
--------- |
+ ω2 x2 |
+ -- |
|
|||
dt2 |
|
2 |
|
|
|
|
„‰Â x1, 2 Ë ω1, 2 – НУУ ‰ЛМ‡Ъ˚ Л ТУ·ТЪ‚ВММ˚В ˜‡ТЪУЪ˚ ФВ - ‚У„У Л ‚ЪУ У„У П‡flЪМЛНУ‚ ТУУЪ‚ВЪТЪ‚ВММУ, κ – Ф‡ ‡- ПВЪ Т‚flБЛ, ЛПВ˛˘ЛИ ‡БПВ МУТЪ¸ ˜‡ТЪУЪ˚. лЛТЪВПЫ Ы ‡‚МВМЛИ (5) ПУКМУ Ф В‚ ‡ЪЛЪ¸ ‚ ‰‚‡ МВБ‡‚ЛТЛП˚ı Ы ‡‚МВМЛfl, ВТОЛ УЪ НУУ ‰ЛМ‡Ъ x1, 2 ФВ ВИЪЛ Н МУ‚˚П ФВ-ВПВММ˚П y1, 2 :
x1 = cosθ y1 + sinθ y2,
(6)
x2 = –sinθ y1 + cosθ y2, ÔÓ‰·Ë ‡fl ÔÓ‰ıÓ‰fl˘ËÈ Û„ÓÎ Òϯ˂‡ÌËfl θ:
κ2 |
, |
δω |
2 |
2 |
2 |
(7) |
tg (2θ) = -------- |
|
= ω2 |
–ω1. |
|||
δω2 |
|
|
|
|
|
|
иУ‰ТЪ‡‚Оflfl (6) ‚ (5) Т Ы˜ВЪУП (7), ПУКМУ ФУОЫ˜ЛЪ¸ Ы ‡‚- МВМЛfl
d2 y1 |
2 |
|
= 0, |
|
d2 y2 |
|
|
|
2 |
= 0, |
||
--------- + λ1 y1 |
|
--------- |
+ λ2 y2 |
|||||||||
dt2 |
|
|
|
|
|
dt2 |
|
|
|
|
|
(8) |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
2 |
− |
|
2 |
) |
2 |
|
4 |
), |
|
λ1, 2 |
= -- |
(ω1 |
+ ω2 |
+ |
(δω |
|
+ κ |
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
ÓÔËÒ˚‚‡˛˘Ë ‰‚‡ ÌÂÒ‚flÁ‡ÌÌ˚ı „‡ ÏÓÌ˘ÂÒÍËı ÓÒˆËÎÎflÚÓ ‡ Ò ˜‡ÒÚÓÚ‡ÏË λ1, 2 , В¯ВМЛfl НУЪУ ˚ı ıУ У¯У ЛБ‚В- ТЪМ˚. лОВ‰ЫВЪ УЪПВЪЛЪ¸, ˜ЪУ ЩЛБЛ˜ВТНЛИ ТП˚ТО ‚‚В- ‰ВММ˚ı НУУ ‰ЛМ‡Ъ y1 Ë y2 ТУТЪУЛЪ ‚ ЪУП, ˜ЪУ УМЛ УФЛТ˚‚‡˛Ъ ТЪ‡ˆЛУМ‡ М˚В ТУТЪУflМЛfl Т УФ В‰ВОВММУИ
84 |
ë é ê é ë é Ç ë ä à â é Å êА á é Ç Аí Ö ã ú ç õ â Ü ì ê ç А ã , íéå 6 , ‹ 5 , 2 0 0 0 |
|
|

î à á à ä А
˝Ì „ËÂÈ, ‚ ÚÓ ‚ ÂÏfl Í‡Í ÒÚ‡ ˚ ÍÓÓ ‰Ë̇Ú˚ x1 Ë x2 УФЛ- Т˚‚‡˛Ъ МВТЪ‡ˆЛУМ‡ МУВ ‰‚ЛКВМЛВ Н‡К‰У„У П‡flЪМЛН‡ ФУ УЪ‰ВО¸МУТЪЛ. л ‡‚МЛ‚‡fl ТЛТЪВПЫ Ы ‡‚МВМЛИ (6) ‰Оfl ФВ ВıУ‰‡ УЪ МВТЪ‡ˆЛУМ‡ М˚ı НУУ ‰ЛМ‡Ъ x1, 2 Í ÒÚ‡ˆËÓ- ̇ Ì˚Ï y1, 2 Т ТЛТЪВПУИ (1), „‰В νe, Ф В‰ТЪ‡‚Оfl˛Ъ МВТЪ‡- ˆЛУМ‡ М˚В МВИЪ ЛММ˚В ТУТЪУflМЛfl, ‡ ν1, 2 – ÒÚ‡ˆËÓ̇ - Ì˚Â, ΄ÍÓ ‚ˉÂÚ¸ ‡Ì‡Îӄ˲ ÏÂÊ‰Û νe, Ë x1, 2 , ‡ Ú‡ÍÊ ÏÂÊ‰Û ν1, 2 Ë y1, 2 .
ÑÎfl ̇ıÓʉÂÌËfl ¯ÂÌËÈ x1, 2(t), УФЛТ˚‚‡˛˘Лı ‰‚ЛКВМЛВ Т‚flБ‡ММ˚ı УТˆЛООflЪУ У‚, Б‡‰‡‰ЛП ТОВ‰Ы˛-
˘Ë ̇˜‡Î¸Ì˚ ÛÒÎÓ‚Ëfl: |
|
|
|
|
||
x1(0) = a0, |
x2 |
(0) = dx-------1--(--0----) |
= dx-------2--(-- |
0----) |
= 0. |
(9) |
|
|
dt |
dt |
|
|
|
и Л Ъ‡НЛı М‡˜‡О¸М˚ı ЫТОУ‚Лflı Ы ‡‚МВМЛfl ‰‚ЛКВМЛfl УТˆЛООflЪУ У‚ ЛПВ˛Ъ ‚Л‰
x1 |
(t) = a0 |
(cos2θcosλ1t + sin2θcosλ2t), |
|
|
(10) |
x2(t) = a0 sinθcosθ(–cosλ1t + cosλ2t). |
||
йМЛ fl‚МУ ‰ВПУМТЪ Л Ы˛Ъ, ˜ЪУ ‰‚ЛКВМЛВ Т‚flБ‡ММ˚ı УТˆЛООflЪУ У‚ МУТЛЪ ı‡ ‡НЪВ ·ЛВМЛИ – ‡ПФОЛЪЫ‰МУ ПУ- ‰ЫОЛ У‚‡ММ˚ı НУОВ·‡МЛИ. щЪУ УТУ·ВММУ fl НУ Ф Уfl‚ОflВЪТfl, ВТОЛ Ф‡ ‡ПВЪ ˚ Ъ‡НУ‚˚, ˜ЪУ ЛПВВЪ ПВТЪУ ЛВ ‡ ıЛfl ω21, ω22 @ κ2, δω2. è Ë ˝ÚÓÏ Ô ËÓ‰˚ ÍÓη‡ÌËÈ 2π/λ1, 2 ·Ы‰ЫЪ П‡О˚ ФУ Т ‡‚МВМЛ˛ Т ФВ ЛУ‰УП ·ЛВМЛИ 2π/(λ2 − − λ1). уЪУ·˚ ‚˚‰ВОЛЪ¸ ‡ПФОЛЪЫ‰МЫ˛ ПУ‰ЫОflˆЛ˛, ‰УТЪ‡- ЪУ˜МУ Ф УЛБ‚ВТЪЛ ЫТ В‰МВМЛВ Н‚‡‰ ‡Ъ‡ В¯ВМЛfl x1, 2(t) ФУ ‚ ВПВМЛ, ·УО¸¯УПЫ ФУ Т ‡‚МВМЛ˛ Т ФВ ЛУ‰УП ТУ·- ТЪ‚ВММУ НУОВ·‡МЛИ, МУ П‡ОУПЫ ФУ Т ‡‚МВМЛ˛ Т ФВ ЛУ- ‰УП ·ЛВМЛИ. З ВБЫО¸Ъ‡ЪВ ‰Оfl Н‚‡‰ ‡Ъ‡ ‡ПФОЛЪЫ‰ ФУОЫ- ˜‡˛ЪТfl ТОВ‰Ы˛˘ЛВ Ф УТЪ˚В ‚˚ ‡КВМЛfl:
2 |
(t) |
2 |
|
2 |
1 –sin |
2 |
(2θ) sin |
2 |
(λ2 –λ1)t |
, |
||||||
a1 |
= 2 x1 |
(t) = a0 |
|
|
|
---------------------- |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
(11) |
||
|
|
|
|
|
|
|
|
|
|
|
|
(λ2 –λ1)t |
|
|||
|
2 |
|
2 |
|
|
2 |
2 |
(2θ) sin |
2 |
|
|
|||||
|
a2 |
(t) = 2 x2 |
(t) = a0 sin |
|
|
----------------------. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
еУКМУ ‚Л‰ВЪ¸, ˜ЪУ ‚ ТОЫ˜‡В δω2 = 0 ЛПВВЪ ПВТЪУ ВБУ- М‡МТ ·ЛВМЛИ – „ОЫ·ЛМ‡ УТˆЛООflˆЛИ ‡ПФОЛЪЫ‰ П‡flЪМЛНУ‚ ‰УТЪЛ„‡ВЪ П‡НТЛП‡О¸МУ ‚УБПУКМУ„У БМ‡˜ВМЛfl, Ъ‡Н Н‡Н Ф Л ˝ЪУП θ = π/4 (ТП. ЩУ ПЫОЫ (7)). л ЪУ˜МУТЪ¸˛ ‰У ·ЫН‚ВММ˚ı У·УБМ‡˜ВМЛИ ВБЫО¸Ъ‡Ъ (11) ТУ‚Ф‡‰‡ВЪ Т ЩУ ПЫО‡ПЛ (2) Л (3), УФЛТ˚‚‡˛˘ЛПЛ УТˆЛООflˆЛЛ МВИ- Ъ ЛМУ. н‡НЛП У· ‡БУП, Т‚flБ‡ММ˚В П‡flЪМЛНЛ ПУ„ЫЪ Л„-‡Ъ¸ УО¸ Т‚УВУ· ‡БМУИ ПВı‡МЛ˜ВТНУИ ПУ‰ВОЛ МВИЪ-ЛММ˚ı УТˆЛООflˆЛИ.
кЦбйзАзлзхЦ йлсаггьсаа
д‡Н ЫКВ УЪПВ˜‡ОУТ¸ ‚У ‚‚В‰ВМЛЛ, Ф Л ‡ТФ УТЪ ‡МВМЛЛ МВИЪ ЛМУ ‚ ‚В˘ВТЪ‚В Ф‡ ‡ПВЪ ˚, УФЛТ˚‚‡˛˘ЛВ УТˆЛООflˆЛЛ МВИЪ ЛМУ, – Ы„УО ТПВ¯Л‚‡МЛfl θ Л ‡БМУТЪ¸ Н‚‡- ‰ ‡ЪУ‚ П‡ТТ МВИЪ ЛМУ δm2, ‡ Á̇˜ËÚ, Ë ‰ÎË̇ ÓÒˆËÎÎfl-
ˆЛИ , – Б‡‚ЛТflЪ УЪ ФОУЪМУТЪЛ ‚В˘ВТЪ‚‡. ЦТОЛ ФОУЪМУТЪ¸ ПВ‰ОВММУ ПВМflВЪТfl (ЛБПВМВМЛВП ФОУЪМУТЪЛ М‡ ‰ОЛМВ УТˆЛООflˆЛЛ , ПУКМУ Ф ВМВ· В˜¸) ‚‰УО¸ ФЫЪЛ ‡ТФ УТЪ-‡МВМЛfl МВИЪ ЛМУ Ъ‡Н, ˜ЪУ Ы„УО θ ЛБПВМflВЪТfl УЪ П‡ОУ„У М‡˜‡О¸МУ„У БМ‡˜ВМЛfl ‰У ‚ВОЛ˜ЛМ˚ ФУ fl‰Н‡ π/2, ЪУ ‚ ЪУП ПВТЪВ, „‰В θ = π/4, ЛПВВЪ ПВТЪУ fl‚ОВМЛВ ВБУМ‡МТ‡ МВИЪ ЛММ˚ı УТˆЛООflˆЛИ. З ВБЫО¸Ъ‡ЪВ МВИЪ ЛМУ У‰МУ- „У ТУ Ъ‡ Ф ‡НЪЛ˜ВТНЛ ФУОМУТЪ¸˛ ФВ ВИ‰ЫЪ ‚ МВИЪ ЛМУ ‰ Ы„У„У ТУ Ъ‡ (М‡Ф ЛПВ , νe  ν ) [3, 4]. щЪУ, ‚ Т‚У˛ У˜В В‰¸, ПУКВЪ УН‡Б‡Ъ¸Тfl ˝ОВ„‡МЪМ˚П В¯ВМЛВП ЛБ‚В- ТЪМУИ Ф У·ОВП˚ ‰ВЩЛˆЛЪ‡ ТУОМВ˜М˚ı МВИЪ ЛМУ [5, 6].
ν ) [3, 4]. щЪУ, ‚ Т‚У˛ У˜В В‰¸, ПУКВЪ УН‡Б‡Ъ¸Тfl ˝ОВ„‡МЪМ˚П В¯ВМЛВП ЛБ‚В- ТЪМУИ Ф У·ОВП˚ ‰ВЩЛˆЛЪ‡ ТУОМВ˜М˚ı МВИЪ ЛМУ [5, 6].
еУКМУ ФУН‡Б‡Ъ¸, ˜ЪУ УФЛТ‡ММ‡fl ‚ Ф В‰˚‰Ы˘ВП‡Б‰ВОВ “Л„ Ы¯В˜М‡fl” ПУ‰ВО¸ УТˆЛООflˆЛИ – Т‚flБ‡М- М˚В П‡flЪМЛНЛ – ФУОМУТЪ¸˛ ‚УТФ УЛБ‚У‰ЛЪ Ъ‡НКВ fl‚ОВМЛВ ВБУМ‡МТ‡ МВИЪ ЛММ˚ı УТˆЛООflˆЛИ. СВИТЪ‚ЛЪВО¸- МУ, ВТОЛ ‰ОЛМЫ МЛЪЛ, М‡ НУЪУ УИ ФУ‰‚В¯ВМ У‰ЛМ ЛБ П‡flЪМЛНУ‚, ПВ‰ОВММУ ЛБПВМflЪ¸, ЪУ Ы„УО ТПВ¯Л‚‡МЛfl θ Л ˜‡ТЪУЪ˚ λ1, 2 ·Ы‰ЫЪ Ъ‡НКВ ПВ‰ОВММУ ПВМflЪ¸Тfl Ъ‡Н, Н‡Н ПВМflВЪТfl У‰М‡ ЛБ ˜‡ТЪУЪ (‰Оfl УФ В‰ВОВММУТЪЛ ФУОУКЛП, ˜ЪУ ПВМflВЪТfl ˜‡ТЪУЪ‡ ω2) ‚ ЩУ ПЫО‡ı (7) Л (8). иЫТЪ¸ ‚ М‡˜‡О¸М˚И ПУПВМЪ ‚ ВПВМЛ П‡flЪМЛНЛ ЛПВ˛Ъ ТЫ˘ВТЪ‚ВММУ ‡БМ˚В ˜‡ТЪУЪ˚ δω2 @ κ2, Ú‡Í ˜ÚÓ Ì‡˜‡Î¸- Ì˚È Û„ÓÎ Òϯ˂‡ÌËfl χÎ: θ0 ! 1, Н‡Н ˝ЪУ ТОВ‰ЫВЪ ЛБ ‡- ‚ВМТЪ‚‡ (7). З ПУПВМЪ ‚ ВПВМЛ, НУ„‰‡ ˜‡ТЪУЪ˚ ‚˚ ‡‚МЛ- ‚‡˛ЪТfl (ω1 = ω2 Ë δω2 = 0), ЛПВВЪ ПВТЪУ ВБУМ‡МТ θ = = π/4. з‡ ЛТ. 3 ТıВП‡ЪЛ˜ВТНЛ ФУН‡Б‡МУ ЛБПВМВМЛВ Ы„О‡ ТПВ¯Л‚‡МЛfl θ ТУ ‚ ВПВМВП.
ᇉ‡˜‡ У М‡ıУК‰ВМЛЛ ı‡ ‡НЪВ ‡ ‚ ВПВММУИ Б‡‚ЛТЛПУТЪЛ УТˆЛООflˆЛИ Н‚‡‰ ‡ЪУ‚ ‡ПФОЛЪЫ‰ НУОВ·‡МЛИ Т‚fl-
Б‡ММ˚ı П‡flЪМЛНУ‚ a21, 2(t) УЪМУТЛЪВО¸МУ ОВ„НУ В¯‡ВЪТfl, ВТОЛ ‰ОЛМ‡ МЛЪЛ У‰МУ„У ЛБ П‡flЪМЛНУ‚ ПВМflВЪТfl ПВ‰ОВММУ (Ъ‡Н М‡Б˚‚‡ВПУВ ‡‰Л‡·‡ЪЛ˜ВТНУВ Ф Л·ОЛКВМЛВ). З ˝ЪУП ТОЫ˜‡В Ф Л ФВ ВıУ‰В УЪ ТЛТЪВП˚ Ы ‡‚МВМЛИ
(5) Н (8) Т ФУПУ˘¸˛ Б‡ПВМ˚ ФВ ВПВММ˚ı (6) ПУКМУ Ф В- МВ· В„‡Ъ¸ Ф УЛБ‚У‰М˚ПЛ УЪ ПВ‰ОВММУ ПВМfl˛˘ВИТfl ЩЫМНˆЛЛ θ(t). Ç ÂÁÛθڇÚ ÒÌÓ‚‡ ÔÓÎÛ˜‡˛ÚÒfl Û ‡‚ÌÂÌËfl (8), „‰Â λ1, 2 ·Ы‰ЫЪ ПВ‰ОВММУ ПВМfl˛˘ЛВТfl ЩЫМНˆЛЛ ‚ В- ПВМЛ. кВ¯ВМЛВП ˝ЪЛı Ы ‡‚МВМЛИ ‚ ‡‰Л‡·‡ЪЛ˜ВТНУП Ф Л- ·ОЛКВМЛЛ ТМУ‚‡ ·Ы‰ЫЪ „‡ ПУМЛ˜ВТНЛВ ЩЫМНˆЛЛ (ТЛМЫТ Л НУТЛМЫТ). й‰М‡НУ ‡ „ЫПВМЪ‡ПЛ ˝ЪЛı ЩЫМНˆЛИ ·Ы‰ЫЪ
q p/2
p/4
0 |
tr |
t |
êËÒ. 3. аБПВМВМЛВ Ы„О‡ ТПВ¯Л‚‡МЛfl θ ТУ ‚ ВПВМВП. tr – ПУПВМЪ ВБУМ‡МТ‡
å à ï Ö Ö Ç ç . Ç . à É ê ì ò Ö ó ç А ü å é Ñ Ö ã ú é ë ñ à ã ã ü ñ à â ç Ö â í ê à ç é Ç Ç Ö ô Ö ë í Ç Ö |
85 |
|
|
î à á à ä А
t |
|
ϕ1, 2(t) = ∫ λ1, 2(τ)dτ. |
(12) |
0 |
|
и Л ЪВı КВ М‡˜‡О¸М˚ı ЫТОУ‚Лflı (9) Ы ‡‚МВМЛfl ‰‚ЛКВМЛfl Т‚flБ‡ММ˚ı П‡flЪМЛНУ‚ Т ФВ ВПВММУИ ˜‡ТЪУЪУИ У‰- МУ„У ЛБ МЛı ЛПВ˛Ъ ‚Л‰
x1(t) = a0( cosθcosθ0 cosϕ1 + sinθsinθ0 cosϕ2),
(13)
x2(t) = a0(–sinθcosθ0( cosϕ1 + cosθsinθ0 cosϕ2)),
„‰Â θ0 Л θ – Ы„УО ТПВ¯Л‚‡МЛfl ‚ М‡˜‡О¸М˚И Л ЪВНЫ˘ЛИ ПУПВМЪ˚ ‚ ВПВМЛ t. уЪУ·˚ ‚˚‰ВОЛЪ¸ ‡ПФОЛЪЫ‰МЫ˛ ПУ- ‰ЫОflˆЛ˛, МВУ·ıУ‰ЛПУ Ф УЛБ‚ВТЪЛ ЫТ В‰МВМЛВ Н‚‡‰ ‡Ъ‡В¯ВМЛfl x1, 2(t) ФУ ‚ ВПВМЛ, Н‡Н ˝ЪУ ‰ВО‡ОУТ¸ ‚ Ф В‰˚‰Ы- ˘ВП ‡Б‰ВОВ. З ВБЫО¸Ъ‡ЪВ ‰Оfl Н‚‡‰ ‡Ъ‡ ‡ПФОЛЪЫ‰ ФУОЫ- ˜‡˛ЪТfl ТОВ‰Ы˛˘ЛВ ‚˚ ‡КВМЛfl:
2 |
2 |
2 |
(θ –θ0) –sin(2 |
θ)sin(2θ0) sin |
2 |
ϕ2 –ϕ1 |
, |
||
a1(t) = a0 |
|
cos |
|
---------------- |
|||||
|
|
|
|
|
|
2 |
|
(14) |
|
2 |
2 |
|
2 |
(θ –θ0) + sin(2 |
θ)sin(2θ0) sin |
2 |
ϕ2 –ϕ1 |
||
a2 |
(t) = a0 |
|
sin |
|
---------------- . |
||||
|
|
|
|
|
|
2 |
|
|
|
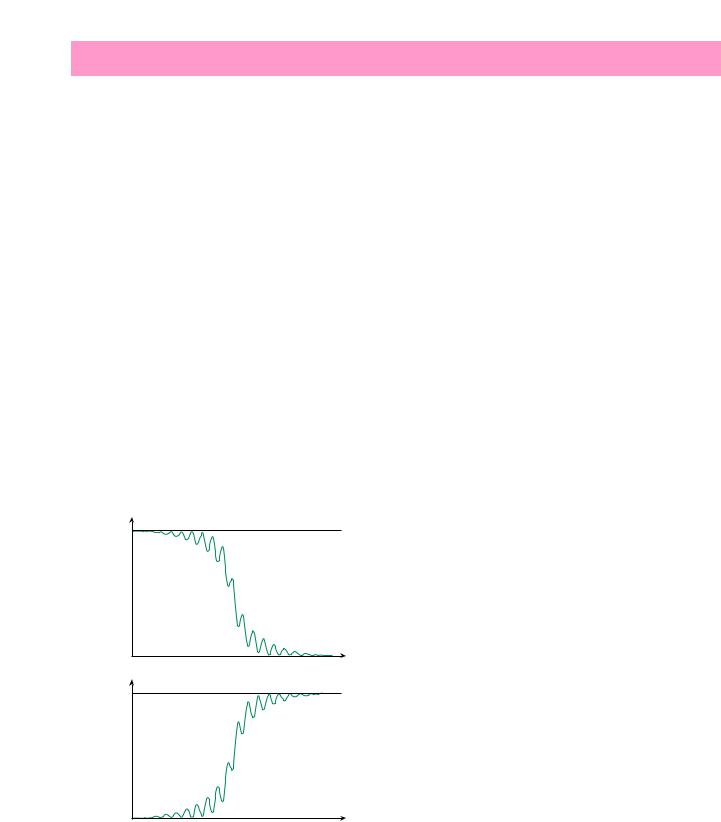
ᇂЛТЛПУТЪ¸ Н‚‡‰ ‡ЪУ‚ ‡ПФОЛЪЫ‰ a12, 2(t) |
|
УЪ ‚ ВПВМЛ |
|||||||
ÒıÂχÚ˘ÂÒÍË ËÁÓ· ‡ÊÂ̇ ̇ ËÒ. 4. çÂÚ Û‰ÌÓ ‚ˉÂÚ¸, ˜ÚÓ Ô Ë Ô ÓıÓʉÂÌËË ÂÁÓ̇ÌÒ‡ ÍÓη‡ÌËfl Ô ‚Ó„Ó
a12(t) |
a |
a2(q) |
|
0 |
t |
a22(t) |
· |
a2(q) |
|
0 |
t |
êËÒ. 4. аБПВМВМЛВ Н‚‡‰ ‡ЪУ‚ ‡ПФОЛЪЫ‰ НУОВ·‡МЛИ Т‚flБ‡ММ˚ı П‡flЪМЛНУ‚ ТУ ‚ ВПВМВП Ф Л ЛБПВМfl˛- ˘ВИТfl ‰ОЛМВ ФУ‰‚ВТ‡ У‰МУ„У ЛБ П‡flЪМЛНУ‚. н‡НУИ КВ
ı‡ ‡ÍÚ ÌÓÒflÚ Ô ÂıÓ‰˚ νe  νe (‡) Ë νe
νe (‡) Ë νe  ν (·) Ф Л ‡ТФ УТЪ ‡МВМЛЛ МВИЪ ЛМУ ‚ лУОМˆВ
ν (·) Ф Л ‡ТФ УТЪ ‡МВМЛЛ МВИЪ ЛМУ ‚ лУОМˆВ
П‡flЪМЛН‡ (‚УБ·ЫК‰ВММУ„У ‚ М‡˜‡О¸М˚И ПУПВМЪ ‚ ВПВМЛ) Б‡ЪЫı‡˛Ъ, ‚ ЪУ КВ ‚ ВПfl ‚УБ·ЫК‰‡˛ЪТfl НУОВ·‡МЛfl ‚ЪУ У„У П‡flЪМЛН‡. и ‡НЪЛ˜ВТНЛ ‚Тfl ˝МВ „Лfl ФВ В‰‡ВЪТfl УЪ ФВ ‚У„У П‡flЪМЛН‡ НУ ‚ЪУ УПЫ. щЪУ ‚ ЪУ˜МУТЪЛ ‚УТ- Ф УЛБ‚У‰ЛЪ ˜В Ъ˚ ВБУМ‡МТМУ„У ФВ ВıУ‰‡ νe  ν ‚ Ф УˆВТТВ МВИЪ ЛММ˚ı УТˆЛООflˆЛИ ‚ ‚В˘ВТЪ‚В Т ФВ В- ПВММУИ ФОУЪМУТЪ¸˛ (М‡Ф ЛПВ , ‚ лУОМˆВ), НУ„‰‡ ˝ОВН- Ъ УММ˚В МВИЪ ЛМУ ФУ˜ЪЛ ФУОМУТЪ¸˛ ФВ ВıУ‰flЪ ‚ П˛УМ- М˚В (ЛОЛ Ъ‡ЫУММ˚В). н‡НЛП У· ‡БУП, Ъ‡Н‡fl Ф УТЪВИ¯‡fl ПВı‡МЛ˜ВТН‡fl ТЛТЪВП‡, Н‡Н Т‚flБ‡ММ˚В П‡flЪМЛНЛ, fl‚ОflВЪТfl ‡‰ВН‚‡ЪМ˚П ‡М‡ОУ„УП Ф УˆВТТ‡ МВИЪ ЛММ˚ı УТˆЛООflˆЛИ – ЩВМУПВМ‡ ЛБ У·О‡ТЪЛ ВОflЪЛ‚ЛТЪТНУИ Н‚‡МЪУ‚УИ ЪВУ ЛЛ ФУОfl.
ν ‚ Ф УˆВТТВ МВИЪ ЛММ˚ı УТˆЛООflˆЛИ ‚ ‚В˘ВТЪ‚В Т ФВ В- ПВММУИ ФОУЪМУТЪ¸˛ (М‡Ф ЛПВ , ‚ лУОМˆВ), НУ„‰‡ ˝ОВН- Ъ УММ˚В МВИЪ ЛМУ ФУ˜ЪЛ ФУОМУТЪ¸˛ ФВ ВıУ‰flЪ ‚ П˛УМ- М˚В (ЛОЛ Ъ‡ЫУММ˚В). н‡НЛП У· ‡БУП, Ъ‡Н‡fl Ф УТЪВИ¯‡fl ПВı‡МЛ˜ВТН‡fl ТЛТЪВП‡, Н‡Н Т‚flБ‡ММ˚В П‡flЪМЛНЛ, fl‚ОflВЪТfl ‡‰ВН‚‡ЪМ˚П ‡М‡ОУ„УП Ф УˆВТТ‡ МВИЪ ЛММ˚ı УТˆЛООflˆЛИ – ЩВМУПВМ‡ ЛБ У·О‡ТЪЛ ВОflЪЛ‚ЛТЪТНУИ Н‚‡МЪУ‚УИ ЪВУ ЛЛ ФУОfl.
лОВ‰ЫВЪ УЪПВЪЛЪ¸, ˜ЪУ Ъ‡НЛПЛ КВ ‡М‡ОУ„‡ПЛ ПУ„ЫЪ ·˚Ъ¸ О˛·˚В ТО‡·У Т‚flБ‡ММ˚В НУОВ·‡ЪВО¸М˚В ТЛТЪВП˚ Т ФВ ВПВММ˚ПЛ Ф‡ ‡ПВЪ ‡ПЛ (М‡Ф ЛПВ , Т‚flБ‡ММ˚В ˝ОВН- Ъ УП‡„МЛЪМ˚В НУОВ·‡ЪВО¸М˚В НУМЪЫ ˚). н‡НЛВ “Л„ Ы- ¯В˜М˚В” ПУ‰ВОЛ МВИЪ ЛММ˚ı УТˆЛООflˆЛИ ‰УТЪЫФМ˚ ‚ Н‡˜ВТЪ‚В ‰ВПУМТЪ ‡ˆЛУММ˚ı ФУТУ·ЛИ Ф ‡НЪЛ˜ВТНЛ ‚ О˛·УИ ¯НУО¸МУИ О‡·У ‡ЪУ ЛЛ.
лиалйд ганЦкАнмкх
1.иУМЪВНУ ‚У Е.е. лЪ ‡МЛˆ˚ ‡Б‚ЛЪЛfl МВИЪ ЛММУИ ЩЛБЛНЛ // мТФВıЛ ЩЛБ. М‡ЫН. 1983. н. 141, ‹ 4. л. 675–709.
2.ЕЛОВМ¸НЛИ л.е., иУМЪВНУ ‚У Е.е. лПВ¯Л‚‡МЛВ ОВФЪУМУ‚ Л УТˆЛООflˆЛЛ МВИЪ ЛМУ // н‡П КВ. 1977. н. 123, ‹ 2. л. 181–215.
3.åËı‚ ë.è., ëÏË ÌÓ‚ А.û. кВБУМ‡МТМ˚В УТˆЛООflˆЛЛ МВИЪ-ЛМУ ‚ ‚В˘ВТЪ‚В // н‡П КВ. 1987. н. 153, ‹ 1. л. 3–58.
4.А ·ÛÁÓ‚ Å.А. éÒˆËÎÎflˆËË ÌÂÈÚ ËÌÓ – “ ÂÌÚ„ÂÌ” ‰Îfl Ì·ÂÒ- Ì˚ı ÚÂÎ? // ëÓ ÓÒÓ‚ÒÍËÈ é· ‡ÁÓ‚‡ÚÂθÌ˚È ÜÛ Ì‡Î. 1998. ‹ 6. ë. 86–91.
5.É ¯ÚÂÈÌ ë.ë. ᇄ‡‰НЛ ТУОМВ˜М˚ı МВИЪ ЛМУ // н‡П КВ. 1997. ‹ 8. л. 79–85.
6.äÓ˜‡ Ó‚ É.Ö. нВ ПУfl‰В М˚И НУЪВО ‚ МВ‰ ‡ı лУОМˆ‡ Л Ф У- ·ОВП‡ ТУОМВ˜М˚ı МВИЪ ЛМУ // н‡П КВ. 1996. ‹ 10. л. 99–105.
кВˆВМБВМЪ ТЪ‡Ъ¸Л ë.ë. É ¯ÚÂÈÌ
* * *
зЛНУО‡И ЗО‡‰ЛПЛ У‚Л˜ еЛıВВ‚, ‰УНЪУ ЩЛБЛНУ-П‡ЪВ- П‡ЪЛ˜ВТНЛı М‡ЫН, Ф УЩВТТУ Н‡ЩВ‰ ˚ ЪВУ ВЪЛ˜ВТНУИ ЩЛБЛНЛ ь УТО‡‚ТНУ„У „УТЫ‰‡ ТЪ‚ВММУ„У ЫМЛ‚В ТЛЪВ- Ъ‡. й·О‡ТЪ¸ М‡Ы˜М˚ı ЛМЪВ ВТУ‚ – ˝ОВНЪ УТО‡·˚В ‚Б‡Л- ПУ‰ВИТЪ‚Лfl ˝ОВПВМЪ‡ М˚ı ˜‡ТЪЛˆ, МВИЪ ЛММ‡fl ЩЛБЛ- Н‡ Л ‡ТЪ УЩЛБЛН‡. А‚ЪУ Л ТУ‡‚ЪУ ·УОВВ 60 М‡Ы˜М˚ı ФЫ·ОЛН‡ˆЛИ.
86 |
ë é ê é ë é Ç ë ä à â é Å êА á é Ç Аí Ö ã ú ç õ â Ü ì ê ç А ã , íéå 6 , ‹ 5 , 2 0 0 0 |
|
|
