
Шпора по физике5
.doc|
1. Структура оптики Оптика – это раздел физики,изуч-ий оптич. излучение(свет),его распростр. в простр-е и взаимодействие света с вещ-ом. Оптика делится на разделы: 1)геометрич. оптика (лучевая);2)физическая(волновая);3)физиологическая. Геом. оптика решает задачи связанные с формированием световых пучков и построением изображений в оптич. системах. Волн.оптика исходит из представлений о природе света как волны, учитывает явл-ия интерференции, дифракции и полepизации. Волн.оптика хорошо выполняется для длин волн λ→0. Физиологич. оптика изуч. распростр. света в органах зрения жив.организмов. Корпускулярно волновой дуализм: Свет с одной стороны представляет собой поток корпускул(частиц), с др. стороны свет явл. электромагнит. волной. В некоторых явл-ях процессы легче описать исходя из корпус-ых cв-тв света, в др. из волн-ых cв-тв.
Видимый свет лежит в диапазоне от λ=
4∙10-7м (фиолетовый) до λ=7,5∙10-7м (красный).
Свет с λ меньше чем у фиолет. света
наз. ультрофиолетовым.
Свет с λ
больше чем у красного наз. инфракрасным.
Оптич. диапазон включает в себя
ультрофиолет., видимуюи инфракрас.
область. Свет явл. электомагнит.
волной, распростр. в про-ве со скоростью
с=3∙ с=
|
2.Основ. понятия геометр. оптики Точечный
источник света
– это такой источник, размерами
которого можно пренебречь по сравнению
с расстоянием, на котором проявляется
его действие( солнце, звезды).Протяженный
источник света
– множество точечных источников
света.Световой
луч. В
геом. оптике полагается, что энергия
световой волны распростр. вдоль
световых лучей.Световой
пучок -
это множество световых лучей.Гомоцентрические
лучи – это
лучи исходящ. или сходящ. в одной
точке.
Параксиальные лучи (приосевые)
– это лучи, углы м/у которыми пренебрежимо
малы α→0, α ≈ sinα
≈tgα Паралл-ый пучок лучей - параксиал. лучи, у которых α=0.Элементы оптич. системы: линзы, зеркала, линзы.Оптич. системы – множество эл-ов оптич. системы(микроскоп, телескоп) Линза – это прозрач тело окружен. двумя сферич. поверхностями. Глав. оптич. ось – это прямая,
проходящ.
ч/з центр сферич. повер-ей линзы
Побоч. оптич. ось – это любая прямая, проходящ. ч/з оптич. центр линзы О и несовпадающая с глав. Оптич. осью.
|
3. Законы геометр. оптики. Закон отражения Падающий луч, отраженный луч и перпендик-р, восстановленный в т. падения луча границы раздела двух сред, лежат в одной пл-ти. Угол падения = углу отражения α=β. Закон преломления Падающ. луч, преломлен.
луч
и перпен-р, вос-ый к границе раздела
двух сред в т. падения луча, лежат в
одной пл-ти. Отношение sin
угла падения к sin
угла прелом-я есть величина постоян.
для двух дан. cред.
где
n
– показатель преломл-я среды, показ.
во сколько раз скорость света в
Закон независимости световых пучков Если 2 свет. пучка при своем распростр. ∩-ют друг друга, то они будут распростр. в первонач. направлении не возмущая друг друга Закон обратимости световых пучков Если свет пустить в обрат.направлении по направлению распростр. прямого луча, то он пойдет по той же траектории, что и прямой луч. Закон полного отражения Если световой луч пустить из оптически более плотной среды в оптич. менее плотную (из воды в воздух), то при некотором угле наз. углом полн. отражения свет. луч во вторую среду не выйдет, а пойдет вдоль границе раздела двух сред.
если
Закон прямолинейн. распростр. света В оптич. однород. среде свет распростр. прямолинейно Принцип Ферма При распростр. света из одной точки в др., свет идет по такому пути, для прохождения к-го требуется min время.
|
||||||||||||
|
4. Линзы.Построения изображений в тонких линзах.Формала тонкой линзы. Если направить в линзу ║-ный пучок света и если после прохождения линзы явл-ся гомоцентрич-ми, то центр этих вышедших из линзы лучей наз-ся задним фокусом линзы. Если на линзу падает гомоцентр-ий пучок лучей и после прохождения линзы лучи становятся ║-ми, то центр этих входящих в линзу лучей наз-ся передним фокусом линзы. Характерные лучи необходимые для построения изображения в линзах:
Полученные изображения бывают:
Изображение действительное, если пересекаются сами лучи. Изображение мнимое, если пересекаются продолжения лучей.
Г
=
Линзы бывают выпуклыми, вогнутыми. Выпуклые линзы посередине толще, чем по краям. Вогнутые линзы посередине тоньше, чем по краям. Вогнутые линзы обычно бывают собирающими.
Формула
линзы:
a – расстояние м/у предметом и линзой b – расстояние м/у линзой и изображением Линза наз. тонкой, если ее толщина много меньше радиусов сферич. поверх-ей , огранич-их линзу. Формула тонкой линзы:
(
1 дптр – оптич. сила линзы, фокусное расст-ие которой равно 1м
|
5. Микроскоп. Увеличение микроскопа. Микроскоп – это оптич. прибор, предназ-ый для рассмотрения микроскопич. объектов. Ход лучей в микроскопе: V=Vоб *Vок Vоб= Vоб
= Vок
=
V=
Микроскоп состоит из двух короткофокусных линз, наз.объективом и окуляром. Предмет помещается вблизи объектива перед передним фокусом. Изобр-ие, даваемое объективом, служит предметом для окуляра, причем оно должно получиться м/у перед.фокусом и самим окуляром. Изобр-ие, даваемое микроскопом, будет увеличенным, перевернутым мнимым. |
6. Телескоп. Телескоп, так же как и микроскоп, состоит из объектива и окуляра и служит для наблюдения удаленных объектов. Различают 2 типа тел-ов: 1)телескопыпы рефракторы используют в качестве объектива линзы; диаметр окуляра соответствует диаметру зрачка в ночное время(5-8 мм). 2) телескопыпы рефлекторы имеют в качестве объектива сферич. зеркало. Самый большой в мире тел.рефлектор имеет диаметр зеркала 6м. Объектив и окуляр располагаются таким образом в тел.рефракторах, чтобы зад. фокус об-ва совпадал с передним фокусом окуляра.
Условное
увеличение телескопа выражается:
Так наз. “ труба Галелея” в качестве окуляра использует рассеивающую линзу. Разрешающая
способность телескопа
– это
мин. угол м/у двумя объектами, к-ые
можно раздельно разглядеть в телескоп.
|
||||||||||||
|
7. Сферич. и плоские зеркала. Формула сферич. зеркала. Ход лучей в сферич. зеркалах:
sinα
~ tgα,
|
8. Формула одной сферич.поверхности линзы. Рассм.
преломление луча на одной пов-ти
сферич. линзы. Будем считать, что лучи,
падающие на пов-ть линзы явл.
панаксиальными.Пусть
показатель преломления среды
Запишем закон преломления:
|
9. Призма. Угол наименьшего отклонения. Угловая дисперсия призмы. Пусть
луч света падает на призму под углом
ε – прелом. угол призмы δ – угол наименьш. отклонения На
практике призмы выбирают таким
образом, чтобы углы
Ф-ла
позволяет опр-ть показатель преломления
материала призмы по углам δ и ε. Показ.
прелом-ия n
явл. ф-й длины волны
Угол наим. Отклонения призмы явл. ф-й длины волны.Найдем
производную по
Угловая дисперсия призмы показывает вел-ну угла м/у лучами с длинами волн отличающимися на 1. Призмы используются в спектральных приборах. Причем
больше
лучше.Призмы
используются в спектральных приборах.
Причем больше угол дисперсной призмы
|
||||||||||||
|
10. Центрированные оптич. системы. Оптич.
сис. наз. центрированной,
если центры всех ее эл-ов лежат на
одной прямой, к-ая наз.
глав. оптич осью. Для
того, чтобы построить изображение в
центри-ой оптич. сис., необязательно
послед-но строить ход лучей для каждого
эл-та оптич. сис-ы. У оптич. сис. имеются
3 особые точки и 3 осбые пл-ти, задание
к-ых полностью определит св-во сис-мы
и позволит строить эти точки и пл-ти
наз.
1)фокальные точки
2)глав.
точки и глав. пл-ти
3)узловые
точки и пл-ти
Главные точки глав. пл-ти имеют такую особенность, что если предмет расположить в перед. глав. пл-ти, то его изображение получится на зад. глав. пл-ти по вел-не равной самому предмету ( увеличь V=1) Оптическая система и ее схематическое изображение:
Узловые точки и пл-ти обладают такой особенностью, что сопряженные лучи, падающие на сис-му из узловой точки и выходящие из узловой точки, м/у собой ║-ны. Если показатели прелом-ия сред. по обе стороны оптич. сис. одинаковы, то узловые и главные пл-ти совпадают. Если перед. и заднии фокусы лежат на ∞, то оптич. сис-а наз. афокальной или телескопичной. Пример построения изображения в оптич. сис-ме.
|
11. Фотомнтрия. Основы фотометрии. Интенсивность э/м волны. Фотом-ия – это раздел оптики, изуч-ий св-ва излучения, связанные с его энергетич. проявлениями. Подразделяется на объективную и субъек-ую. Объектив. фотом-ия изуч. энергетич. св-ва света по их воздействию на приборы. Субъектив.
фотом-ия
изуч. энергетич. св-ва света, оцениваемые
по зрительному восприятию.
φ
– азимутальный
угол.
Если к-л физ. величина оканчивается на “-сть”(скорость, плотность, яркость и т.д), тогда речь идет о некоторой величине, приходящийся на единицу другой. Спектральная
плотность
относится к
некоторой величине связанной с
излучением и приходящийся на ед-цу
длин волн или частот. Т.к. свет явл.
э/м волной, то энергия света складывается
из энергии электрич. поля и энергии
магнит. поля. Из курса электродинамики
известно, что объем. пл-ть электрич.
поля опред-тся выражением:
Чаще всего рассм. среду – вакуум (ε =1) . Напряженность
электрич. поля световой волны изменяется
по гармонич. закону
ω~
Тогда энергия, заключенная в
объеме
V
равна
Пусть
на расст-ии
r
от источника напряж-ть электр.поля
равна
Если излучение распростр. в поглощающей среде, то с увелич-ем расст-ия от него полн. поток уменьшается. Волновые
пов-ти от точеч. источников имеют вид
сферы. Пусть на расст-ии 1м амплитуда
вектора напряж-ти равна
|
12. Объектив. фотометирч. величины. Объективные
фотометрические величины часто
сопровождаются словами : “энергетический”
или “излучение”. Энергетич.
поток –
это объектив. ф/м в-на. Субъектив. ф/м
в-ны сопровождаются словами: “свет”,
“световой”. Например, световой поток
или сила света. Кроме того, если в
одной и той же задачи встречаются и
объектив. и субъектив. ф/м в-ны, тогда
субъектив. ф/м в-ны сопровождаются
индексом v
( Спектральной
пл-тью интенс-ти
Если взять Интервал длин волн не единич., а произвол. Длины
dλ,
тогда интен-ть излучения, принадлежащая
дан. интервалу, будет опр-ся
|
||||||||||||
|
§13. Энергетическая сила излучения. Понятие
энергетической силы излучения
применима лишь к точечным источникам
излучения либо к источникам небольших
размеров.Если точечный источник света
излучает телесный угол
Изотропный источник – это источник сила света, которого по всем направлениям одинакова. |
§14. Энергетическая яркость излучения. Понятие яркости вводится только для протяженных источников света и характеризует излучение с различных участков поверхности, изучающего тела. Если
участок поверхности
Если
площадка
телесный
угол
|
§15. Энергетическая светимость (R). Излучательная способность. -
это физ.величина численно равная
потоку излучения с единицы поверхности
тела по всем направлениям, т.е телесный
угол
Докажем
соотношение
|
||||||||||||
|
§16. Энергетическая освещенность. Экспозиция. Рассмотрим
поверхность
Экспозицией Н называется произведение энергетического потока Р на время излучения t
|
§17. Субъективные фотометрические величины. Основной
фотометрической объективной величиной
является поток излучения Р. Зная,
поток можно определить все основные
фотометрические величины.Основной
субъективной фотометрической величиной
является сила света
Эталоном
1 Канделлы явл.сила света, даваемая
Сила
света других источников определяется
из соотношений:
Световой
поток
Субъективной
фотометрической величиной является
яркость
Яркость
дневного неба равна
Яркость
нити накаливания в лампе накаливания
Освещенности некоторых поверхностей: - школьный класс >75 лк - экран кинотеатра 100 лк - белая ночь 1 лк -
обычная ночь
При
наблюдении светящихся тел или тел,
рассеивающих свет, наши органы зрения
реагируют на яркость. Яркостные
ощущения зависят от освещенности
сетчатки глаза. Яркостные ощущения
в отсутствии поглощения не зависят
от расстояния до источника света.
Покажем это, пусть источник света
имеет площадь S
и силу света J
и находятся на расстоянии а от
хрусталика глаза. На сетчатке,
расположенной на дне глазного яблока
на расстоянии
|
§18. Спектральная чувствительность глаза. Функция видности. Спектральная световая эффективность. Спектральная световая экономичность. Реальные источники света излучают в широком диапазоне длин волн. Для создания светового потока в 1 лм требуется различная мощность (поток излучения) для длин волн различной длины. Глаз
наиболее чувствителен к длине волны
Спектральная
чувствительность
показывает, какой световой поток в
лм создает поток излучения в 1 Вт
при длине
волны
Формула
Световая
экономичность совпадает со значениями
функции видности. Для источника,
дающего излучение длиной волны только
555 нм световая экономичность равна
1. полная световая экономичность
определяется выражением
- солнце 0,14 - лампа накаливания 0,02 - лампа дневного света 0,06 В случае лампы накаливания полная мощность определяется произведением тока на напряжение.
|
||||||||||||
|
§19. Уравнение волны. Волновая поверхность. Фронт волны. Волновой вектор. Выведем уравнение плоской волны:
Если
в начальный момент времени t
начальная фаза уже имела некоторое
значение
Точечные
источники света дают сферическую
волну. Для сферическую волну значение
Амплитуда сферической волны убывает
обратно пропорционально расстоянию
до источника. Уравнение сферической
волны имеет вид:
Длина волны в среде будет в n раз меньше, чем в вакууме. Т.к в среде длина волны уменьшается в n раз, то для расчета разности фаз нам необходимо длину участка среды l растянуть в n раз, т.е рассматривать явление прохождения волны как будто среды нет, т.е в вакууме.
Забегая
вперед укажем, что при отражении от
границы раздела с более оптически
плотной средой волна приобретает
дополнительную разность хода равную
У плоских волн волновая поверхность представляет собой пл-ть, у сферических волн волновая поверхность представляет собой сферу. |
§20. Интерференция света. Это волновое явление заключается в сложении двух когерентных волн при которых амплитуда резутирующей волны не равна алгебраической сумме амплитуд складанных колебаний.
Рассмотрим следующий случай: 1)
Если разность фаз складываемых колебаний равна 0, то интенсивность полученного колебания в 4 раза больше интенсивности каждого из колебаний. 2)
Если
разность фаз складываемых колебаний
равна
Обычно интерференционная картина имеет вид окружности, полос или линий. |
§21. Примеры расчета интерференционной картины. Пусть имеются двух когерентные источники света. Пусть источники нах-ся на расстоянии d друг от
друга.
Наша задача заключается в том, чтобы
предсказать вид интерференционной
картины и рассчитать некоторые
параметры этой картины.Пусть волны
В
точке х будет наблюдаться минимум
интенсивности, если разность хода
Обычно
Найдем координаты, в которых будет наблюдаться максимум
Вид
интерференционной картины грани
имеют вид линий, для которых расстояние
до точки
Из
интерференционные полосы будут окрашенными кроме полосы нулевого порядка.
|
||||||||||||
|
§22. Принцип Гюйгенса. Каждая точка среды, до которой доходит волновое возмущение сама становится источником вторичных волн, огибающие этих вторичных волн является волновым фронтом в следующий момент времени. Интенсивность волны в любой точке пространства определяется интерференцией вторичных волн. принцип Гюйгенса позволяет предсказать явление дифракции света также то, что маленькие отверстия на пути света становятся источниками вторичных волн. Недостатки принципа. Он не позволяет определить интенсивность света в том или ином месте пространства. Так по принципу Гюйгенса волна может идти в обратном направлении, хотя интенсивность света в этом направлении равна 0.
|
§23. Интерференция в тонких пленках и пластинках. Радужные полоски наблюдается на поверхности малых пузырей, на поверхности воды на которой разлита нефть или масло, т.е будет наблюдаться интерференционная картина при отражении света от внешней и внутренней поверхности воды (мыльный пузырь) или нефти.Рассмотрим точечный источник света
Если
лучи
когерентными, то в точке В будет наблюдаться устойчивый максимум или минимум. Другие
пары лучей от источника
Может
оказаться что
Рассчитаем
разность фаз лучей
Разность хода при отражении от плоской параллельной пластинки.
|
|
||||||||||||
|
24.Кольцо Ньютона. Кольца Н. Являются примером полос равной толщины.
Точка
Р рядом с выпуклой поверхностью
линзы.Опр-им расстояние от т.О до точки
в которой будет наблюдаться минимум
интенсивности.Разность хода для
минимума опр-ся выражением:
Кольца расположены чаще при большем значении m.
|
25.Дифракция света.Метод Зон Фринеля. Дифракция-это огибания волной препятствий и попадания света в область геом. тени.В более широком смысле под дифракцией понимают комплекс явлений связанных с отклонением света от законов геом. оптики.Дифракция наблюдается при прохождении света вблизи резких неоднородностей среды(на краях преград,вблизи малых отверстий и т.д.).Пусть имеется некоторый фронт волны площадью S. Наша цель определить значение вектора напряженности
электромагнитной волны(интенсивности
света)в точке наблюдения Р.Пусть
амплитуда напряжнности в любой точке
волны=
|
26.Дифракционная картина от простейших преград. 1.Дифракция на круглом отверстии.Поставим на пути сферич. волны круглое отверстие,которое открывает m первую зону Фринеля.За отверстием расположен экран. Рассчитаем значение вектора
напряженности
в точке наблюдения Р.
2.Дифракция на круглом диске. Пусть диск перекрывает m первых зон Фринеля. Определим значение освещенности в точке наблюдения Р.
3.Дифракция на краю полуплоскости. Разобьем волновой фронт на ряд зон для каждой точки экрана будет свое разбиение. Пользуясь методом зон Фринеля также можно рассчитать значение интенсивности. 4.Дифракция Фраунгофера. Рассмотрим
распределение интенсивности на экране
в случае дифракции Фраунгофера.Дифракция
Ф. отличается от дифракции Фринеля
тем,что интерферирует параллельные
лучи.В это случае источник света
устан. на бесконечности,тогда он дае
параллельные лучи.Для наблюдения
этого вида дифракции используют
собирательную линзу.Пусть ширина
щели равна
Эта формула минимума интенсивности для дифракции на одной щели.
|
||||||||||||
|
27.Дифрационная решетка. Дифракционная решетка-это прозрачная пластина на которую нанесены непрозрачные штрихи,представляющие собой совокупность узких щелей;расстояние между соседними щелями называется периодом дифракционной решетки.
максимум
|
28.Виды поляризации света. Различают
два вида света:естественный и
поляризованный.Естеств-ый
свет-свет
у которого вектора напряженности эл.
поля
Естеств.
свет обозначают следующим образом:
Свет наз-ся поляризованным,если
вектор напряженности эл. поля
2)вектор
У
света поляризованного по кругу
амплитуда вектора
Циркулярно
поляризованный свет может быть
представлен как суперпозиции двух
линейно поляризованных колебаний,если
их плоскости поляризации взаимно
перпендикулярны и разности фаз
векторов
собой,тогда
при сложении этих колебаний будет
получен севт поляризованный по
эллипсу.Кроме того,оказывается,что
линейно поляризованный свет можно
получить как суперпозицию двух волн
поляризованных по кругу в различных
напрвлениях.Частично
поляризованный свет-это
свет у которого амплитуда вектора
напряженности
Степенью
поляр. света
|
29.Поляризаторы и анализаторы.Закон Малюса. Поляризаторы-приборы
дающие возможность получить
поляризованный свет.Анализаторы-это
приборы с помощью которых можно
проанализировать является ли свет
поляризованным или нет.Конструктивно
поляризатор и анализатор это одно и
тоже.З-н
Малюса.Пусть
на поляризатор падает свет интенсивности
Очевидно
интенсивность света вышедшего из
поляризатора будет равна
|
||||||||||||
|
30.Способы получения поляризованного света.Закон Брюстера. Как
показывает опыт при преломлении и
отражении света преломленный и
отраженный свет оказывается
поляризованными,причем отраж. свет
может быть полностью поляризоанным
при некотором угле падения
Угол падения при котором отраж.
свет является полностью поляризованным
назвается углом
Брюстера.Угол
Брюстера определяется из закона
Брюстера:
|
31.Прохождение света в анизотропных средах. Двойное лучи-преломление. Для некоторых кристаллов у которых решетка не имеет форму куба (NaCl) то наблюдаются такие явления: узкий пучок падающего излучения может раздвоятся после прохождения кристалла, причем плоскости поляризации выходящих пучков при этом будут взаимно перпендикулярны. В некоторых случаях раздвоение не наблюдается и выходящий пучок поляризированным не будет(если входящий не был поляризован). Самым ярким представителем кристаллов этого типа является исландский испат(CaCO3), элементарная ячейка которого представляет ромбоэдр, т.е. куб сплюснутый в направлении двух противоположных вершин.
Прямая ОО’ является оптической осью кристалла. Кристалл можно распилить следующим образом: 1) грани параллельны главной оптической оси; 2) грани перпендикулярны главной оптической оси ; 3) грани расположены под некоторым углом к главной оптической оси.
Оптическая ось определяет некоторое выделенное направление в кристалле. Главной плоскостью или главным сечением кристалла называется плоскость образованная падающим на кристалл лучом и оптической осью кристалла. Если луч света падает перпендикулярно на грань кристалла в случае 3) то наблюдается два выходящих пучка света. Первый луч ведет себя
обычным образом поэтому его называют
обыкновенным.
Второй луч ведет себя необычно, поэтому
его называют необыкновенным.
В этом случае когда свет падает на
кристалл не перпендикулярно, а под
некоторым углом к грани так же
наблюдается раздвоение пучка на о и
е. В этом случае обыкновенный луч
будет являться поляризованным
перпендикулярно к главной плоскости
кристалла, а необыкновенный луч будет
поляризованным параллельно к главной
плоскости кристалла. Оказывается
показатель преломления кристалла
для о и е лучей не равны между собой
|
32.Квантовая природа излучения. Квантовая
гипотеза Планка:излучение
поглощения света происходит не
непрерывно,а дискретно,т.е.опр-ми
порциями-квантами энергия которых
определяется частотой
|
||||||||||||
|
33.Закон Стефана Больцмана. Энергетическая
светимость черного тела пропорционально
четвертой степени термодинамической
температуры,т.е с понижением температуры нагретых
тел в их спектре все сильнее преобладает
длинно волновое излучение.Зависимость
максимальной спектральной плотности
энергетической светимости черного
тела от температуры определяется
выражением
|
34.Внешний фотоэффект.Законы фотоэффекта. Внешний
фотоэффект-это
испускание электронов веществом под
действием электромаг. излучения.Уравнение
Эйнштейна для внешнего фотоэффекта:
|
35. Вольт-амперная характеристика фотоэлемента. Это зависимость фототока I образуемого потоком вырванных фотоэлектронов с поверхности катода под действием падающего света от напряжения U между электронами. Для изучения вольтамперной характеристики используется установка Столетова для исследования фотоэффекта: Электроны вырываются с катода под действием света и в зависимости от величины приложенного напряжения достигают или не достигают анода. По мере увеличения напряжения фототок возрастает и все большее число фотоэлектронов достигают анода. График вольтамперной характеристики: Ток насыщения – это ток при котором все вырванные фотоэлектроны достигаю анода. Пологий характер прямых говорит о том, что электроны вылетают с различной начальной скоростью, при напряжении U=0 фототок не исчезает. Он исчезает только при некотором напряжении, которое называется запирающим.
|
||||||||||||
|
36. Характеристики атомного ядра. Ядерные силы. Атомное ядро – положительно заряженная часть атома в которой сосредоточена практически вся ее масса. Все атомные ядра кроме ядра атома водорода состоят из элементарных частиц: протонов и нейтронов, они называются нуклонами. Нуклоны в ядре удерживаются ядерными силами и движутся внутри ядра с не релятивистскими скоростями (меньше скорости света). Протон р – это положительно заряженная частица с зарядом равным элементарному и массой mр = 1,672*10-27 , или mp = 1863me. Нейтрон n – это нейтральная частица с массой покоя mn = 1,675*10-27кг, mn = 1839me, mе = 9,1*10-31кг. Зарядовое число Z – равно числу протонов в ядре. Оно совпадает с порядковым номером элемента в ПС Менделеева. Массовое число А – равно общему количеству нуклонов в атомном ядре. Таким образом количество нейтронов N в ядре можно определить как N = A – Z. Изотопы – это ядра с одинаковыми зарядовыми числами, но различными массовыми числами. Они имеют одинаковые Z, но разные А. Изотоны
– это ядра
с одинаковым числом нейтронов, но с
разным числом протонов и следовательно
с разным массовым числом. ( Изобары – это ядра имеющие одинаковое массовое число. Они имеют разные Z и N. ( Радиус
атомного ядра определяется из
соотношения: Где А – массовое число; R0 = 1,3-1,7 фм = 1,3-1,7*10-15м Энергия связи ядра атома – это энергия, которая необходима для расщепления ядра на отдельные нуклоны. Определяется выражением:
Удельная
энергия связи – это
энергия связи приходящаяся на один
нуклон:
2)являются коротко действующими (действие ядерных сил проявляется только тогда, когда расстояние между нуклонами порядка 10-15м, с увеличением расстояния они быстро уменьшаются до нуля);3)обладают зарядовой независимостью, т. е. не зависят от электрич. зарядов и имеют неэлектрическую природу; 4)имеют способность к насыщению, т. е. каждый нуклон может взаимодействовать только с ограниченным числом нуклонов;5)не являются центральными силами, т. е. их нельзя представить в виде сил действующих от одного центра сил.
|
37. Радиоактивный распад. Закон радиоактивного распада. Радиоактивный распад – это естественное радиоактивное превращение ядер, происходящее самопроизвольно. Атомное ядро испытывающее радиоактивный распад называют материнским, а возникающее ядро – дочерним.Рад. распад – это статистическое явление, которое имеет вероятностный характер.Вероятность распада за единицу времени равно доле ядер распадающихся за одну секунду. Эта величина называется постоянной радиоактивного распада и обозначается λ. следовательно, в единицу времени из огромного количества частиц N распадается в среднем λ* N ядер, эту величину называют активностью нуклида.Закон радиоактивного распада:Число ядер dN распавшихся в среднем за интервал времени (t; t+dt) пропорционально промежутку времени dt и числу ядер N не распавшихся к моменту времени t: dN=- λNdt. Где λ – постоян. рад. распада, знак «-» указывает, что общее число радиоактивных ядер, в процессе уменьшается. Решим данное диф. уравнение:
Период
полураспада
– это промежуток времени за который
исходное число радиоактивных ядер
уменьшается вдвое. Он характеризует
интенсивность процесса распада, т.
е.
Для разных элементов период полураспада лежит в диапазоне: 10-7≤Т1/2≤1018с. |
38. Радиоактивность. Типы радиоактивных излучений. Радиоактивность – это способность некоторых атомных ядер самопроизвольно превращаться в другие ядра, с испусканием различных частиц.Открытие радиоактивности датируется 1896 годом, когда Беккерель обнаружил испускание солями урана неизвестного излучения, которое действовало на фотопластинку, ионизировало воздух и проникало сквозь тонкие металлические пластинки. Радиоактивность делится на естественную (наблюдается у неустойчивых изотопов существующих в природе) и искусственную (наблюдается у изотопов полученных посредством ядерных реакций). Принципиального различия между этими типами излучения нет.Типы радиоактивных излучений:1.α–излучение – поток ядер гелия (Не). Оно обладает высокой ионизирующей и малой проникающей способностью.2.β–излучение – поток быстрых электронов. Обладает низкой ионизирующей способностью и более высокой, по сравнению с α–излучением проникающей способностью.3.γ–излучение – это коротко волновое электромагнитное излучение с очень малой длиной волны λ<10-10м, т.е. представляет собой поток γ–квантов-фотонов. Обладает относительно слабой ионизирующей способностью и огромной проникающей способностью. α–распад – это распад атомных ядер, сопровождающийся испусканием α–частицы. Заряд α–частицы равен +2е; масса α–частицы совпадает с массой ядра гелия.
Масса материнского ядра должна быть больше суммы масс дочернего ядра и α–частицы.α–распад – это свойство тяжелых ядер с А > 200, Z > 82.α–частицы образуются в момент радиоактивного распада при встрече двух движущихся протонов и нейтронов.β–распад – это самопроизвольный процесс превращения радиоактивного ядра в др. ядро. Массовое число при этом не изменяется, а зарядовое число изменяется на ±1. β–распад происходит согласно схеме:
|
||||||||||||
|
39. Модель атома Резерфорда. Постулаты Бора. Опыт Резерфорда по рассеиванию частиц: Поток α–частиц испускался из радиоактивного источника, на пути α–частиц ставилась золотая фольга. α–частицы регистрировались по вспышкам на экране. В результате были обнаружены α–частицы, к-ые после прохождения фольги отклонялись от направлений первоначального распространения на некоторый угол. Также были обнаружены α-частицы, к-ые меняли направление своего движения на 180º. Резерфорд пришел к выводу, что в ядре сосредоточен весь положительный заряд, а вокруг него движутся электроны по орбитали, образуя электронную оболочку, т.к. атомы нейтральные, то заряд ядра равен суммарному заряду электрона. Модель атома Резерфорда не может существовать в рамках классической физики, т.к. электрон вращающийся вокруг ядра должен излучать электромагнитные волны и теряет энергию. В результате электрон должен упасть на ядро. Однако этого не происходит, т.к. атом – частица стабильная. строение атома описывается из квантово механических соображений, в которых законам Ньютона нет места. Постулаты Бора:1.Постулат Бора (Постулат стационарного состояния): В атоме существуют стационарные (не изменяющиеся со временем) состояния, характеризующиеся определенными дискретными значениями энергии. Стационарным состояниям атома состветствуют стационарные орбиты по которым движутся электроны. Находясь в стационарном состоянии атом не излучает. Следствие из 1 постулата Бора: Стационарному
состоянию атома соответствуют
дискретные квантованные значения
момента импульса
|
40. Атом водорода по Бору. Дано: me, e, h; Найти: υ, r, ν, ω, T, Ek, Ep, Eполн - ?
n =1; r1 =h2ε0/πme2; h = 6,62*10-34 Дж*с ε0 = 8,85*10-12 Ф/м т = 9,1*10-31 кг е = 1,6 *10-19кл
|
41. Спектр атома водорода. Т.к. атом водорода при выходе из одного стационарного состояния в другое испускает квант энергии, то частоты излучения принимают также дискретные значения. Согласно экспериментальным данным спектр излучения атома водорода состоит из серий линий частоты которых описываются формулами. Частоты спектральных линий описываются: 1) в ультрафиолетовых областях спектра (Серия Лаймана):
Обобщенная формула Бальмера:
Выше Е∞ равное нулю электрон может иметь любую энергию, т.к. он является свободным, стрелками показаны переходы, приводящие к излучению линий принадлежащих различным сериям спектра атома водорода. Спектр поглощения атома водорода также является линейчатым. При нормальных условиях он содержит только одну серию – серию Лаймана. Это объясняется тем, что при относительно небольшой температуре и незначительном давлении поглощение будет происходить только с первого энергетического уровня, т.е. возникает серия Лаймана.
|
||||||||||||
|
42. Эффект Доплера. Эффект Комптона. Эффект Доплера для электромагнитных волн наблюдается при движении друг относительно друга источника и приемника электромагнитных волн. Закономерности эффекта Доплера для электромагнитных волн устанавливаются на основе специальной теории относительности. Формула
эффекта Доплера: υ – скорость источника света относительно приемника с – скорость света в вакууме θ
– угол между вектором скорости
При θ = 0 наблюдается продольный эффект Доплера
При
θ = π/2
наблюдается
поперечный эффект Доплера, при этом
Эффект Комптона – это упругое рассеивание коротко волнового электромагнитного излучения (рентгеновского или γ-излучения) на свободных или слабосвязанных электронах, сопровождающееся увеличением длины волны. Комптоновский сдвиг - Δλ=|λ–λ′|
Разность длины волны Δλ не зависит от длины волны λ падающего излучения и природы рассеянного вещества, а зависит только от угла θ между направлениями рассеянного и первичного излучений.λ – длина волны падающего излучения; λ′ - длина волны рассеянного излучения. Эффект Комптона необъясним с точки зрения волновых представлений.Эффект Комптона рассматривается как упругое рассеивание фотона на покоищемся электроне. Фотон столкнувшись с электроном передает ему часть энергии и импульса и изменяет направление своего движения.
|
43. корпускулярно-волновая двойственность. Свойства электромагнитного излучения. Явления подтверждающие квантовое представление о природе света:
Явления подтверждающие волновую природу света:
Явления объясняемые как с волновой, так и с корпускулярной теории:
Уравнение связывающее корпускулярные св-ва эл-магн. излучения (энергия и импульс фотона) с волновыми св-ми (частота и длина волны).
Квантовая
теория:
Если электромагнитная волна падает на металл, то под действием эл.поля волны напряженностью Е, электроны будут двигаться в направлении противоположном Е. Магнитное поле с индукцией В элек.-магн. волны действует на движущийся с силой Лоренца (она определяется правилом левой руки) в направлении перпендикулярном поверхности металла, т.е. будет оказывать давление на поверхность металла.Проявление волновых свойств света: чем больше длина волны, тем меньше энергия и импульс фотона и тем труднее обнаруживаются квантовые св-ва света. (существование красной границы фотоэффекта).Проявление корпускулярных свойств света: чем меньше длина, тем больше энергия и импульс фотона, тем труднее проследить волновые св-ва света (например: дифракция рентгеновских лучей обнаруживается только на кристаллических решетках кристаллов).
|
44. Гипотеза де Бройля. Волны де Бройля. Гипотеза
де Бройля: корпускулярно-волновой
дуализм имеет универсальный характер
и распространяется не только на
фотоны, но и на все частицы материи.
Частицы в-ва наряду с корпускулярными
св-ми обладают также волновыми св-ми,
т.е. любая частица является волной,
длина которой определяется длиной
волны де Бройля: Экспериментальное
подтверждение волновых св-в микрочастиц:
1.опыты
Девиссона и Джермера – пучок электронов
рассеивающийся от естественной
дифракционной решетки – кристалла
никеля, дает отчетливую дифракционную
картину, а максимумы дифракционной
картины соответствуют формуле Вульфа
– Бреггова.2.опыты
Тартаковского и Томсона – наблюдалась
дифракционная картина при прохождении
пучка быстрых электронов через
металлическую фольгу толщиной порядка
1мкм = 10-6м.Плоская
волна де Бройля: согласно
корпускулярно-волновому дуализму
материи и гипотезе де Бройля с движением
частицы обладающей определенными
энергией и импульсом, связывается
плоская волна де Бройля, уравнение
которой имеет вид: |
||||||||||||
|
|
|
|
||||||||||||
|
45. Соотношение неопределенностей Гейзенберга. Во многих случаях классические представления (например: в каждый момент времени частица занимает строго определенное место и обладает определенным импульсом) неприменимы для описания микрообъектов. Гейзенберг выдвинул идею по принципиальной невозможности измерения определенных пар связанных между собой величин так, чтобы они одновременно имели точные значения.Соотношение неопределенностей для коор-т и импульсов:ΔхΔрх≥ħ ,ΔyΔрy≥ħ,ΔzΔрz≥ħ .Микрочастица не может иметь одновременно точных значений координаты (x,y,z) и соответствующих компонентов импульса (рх, рy, рz), причем их произведения (неопределенности) не могут быть меньше ħ.Пусть микрочастица находится в точке с точным значением координаты, тогда Δх = 0, тогда Δрх→∞, и наоборот.Соотношение неопределенностей для энергии и времени:ΔEΔt≥ħ, ΔE – неопределенность энергии некоторого состояния системы; Δt - промежуток времени в течение которого оно существует. Из-за
конечности времени жизни атома в
возбужденном состоянии, энергия
атомов не является точно определенной,
поэтому частота излученного фотона
также должна иметь неопределенность
Соотношение неопределенностей является квантовым ограничением применимости классической механики к микрообъектам.
|
46. Временное и стационарное уравнение Шредингера.
Основное уравнение дожно быть уравнением относительно волновой ф-ии: Ψ(x,y,z,t),т.к. именно она определяет вероятность пребывания частицы в момент времени t в данном объеме, т.к. искомое уравнение должно учитывать волновые св-ва частиц, то оно должно быть волновым уравнением, подобно уравнению описывающему электромагн. волны. Временное уравнение Шредингера:
i - мнимая единица.Это уравнение постулируется, а его правильность подтверждается согласием с опытом получаемых результатов.Условия накладываемые на волновую функцию:
Стационарное уравнение Шредингера: В
случае стационарного поля ф-ия U(x,y,z)
не зависит от времени, тогда волновая
ф-ия представляется в виде произведения
двух функций: одна ф-ия только коор-т,
другая ф-ия только времени. Стационарное
уравнение Шредингера после подстановки
этой волновой ф-ии во временное
уравнение Шредингера, получим ψ – коор-ая (амплитудная) часть волновой ф-ииΨ Е – полная энергия частицы U – потенциальная энергия частицы Δ – оператор Лапласа.
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||
|
|
|
|

 ;С другой стороны
;С другой стороны
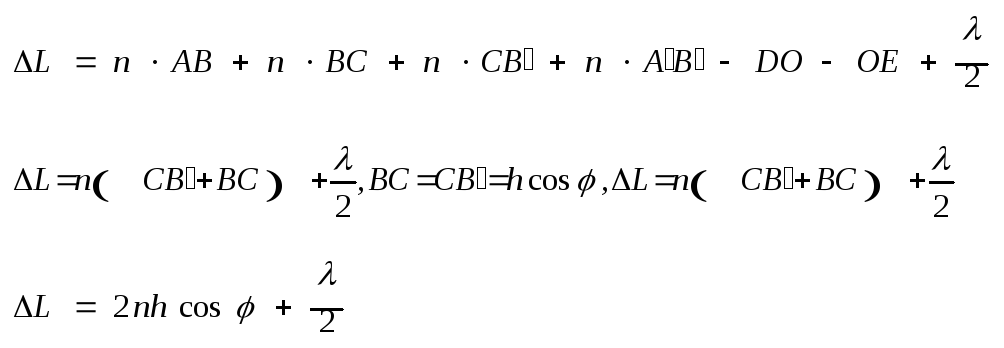

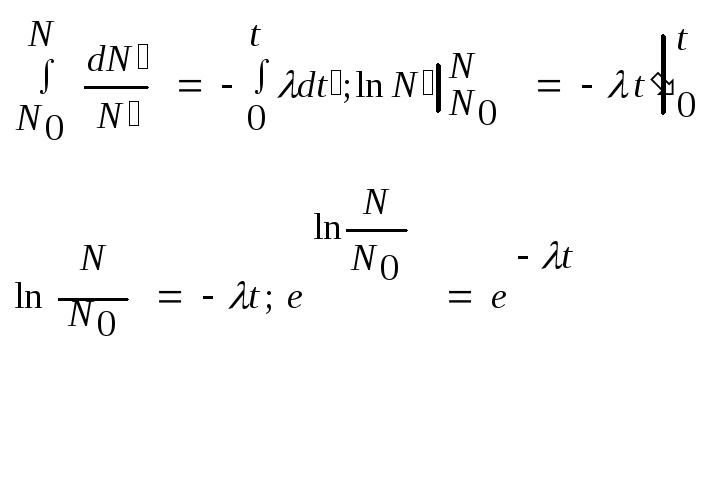 N=
N0e-λt
N0–
начальное
количество нераспавшихся ядер в
момент времени t=0.
N-
число нераспавшихся ядер в момент
времени t
.
N=
N0e-λt
N0–
начальное
количество нераспавшихся ядер в
момент времени t=0.
N-
число нераспавшихся ядер в момент
времени t
.