
- •1. Кинематика поступательного движения.
- •2. Кинематика поступательного и вращательного движения.
- •3. Динамика. Работа, энергия. Законы сохранения.
- •4. Динамика вращательного движения.
- •Примеры решения задач.
- •5. Динамика вращательного движения. Работа, энергия. Законы сохранения энергии и момента импульса.
- •6. Упругие свойства твердых тел.
- •7. Механические колебания и волны.
- •8. Акустика.
- •9. Теория относительности.
- •10. Механика жидкостей и газов.
9. Теория относительности.
![]() –релятивистскоесокращение длины;
–релятивистскоесокращение длины;
 –релятивистское
замедление времени;
–релятивистское
замедление времени;
![]() –энергия
покоя;
–энергия
покоя;
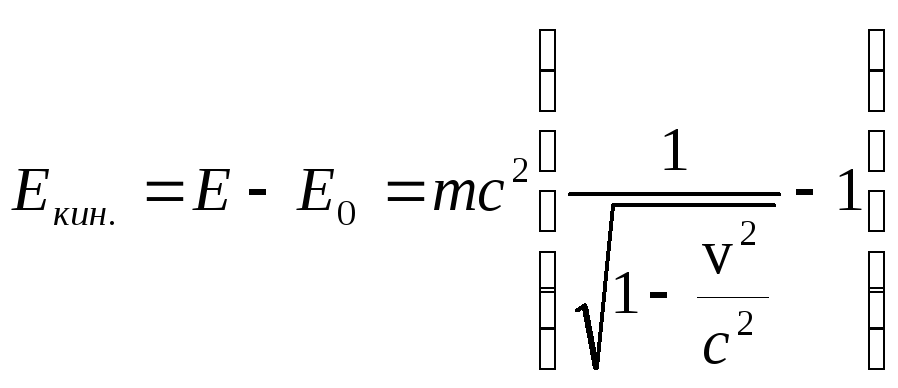 –кинетическая
энергия;
–кинетическая
энергия;
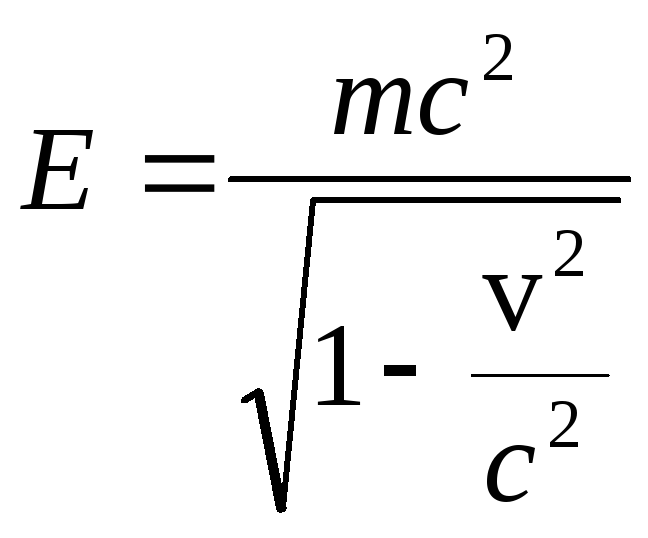 –полная
энергия;
–полная
энергия;
![]() –взаимосвязь
энергии и импульса;
–взаимосвязь
энергии и импульса;
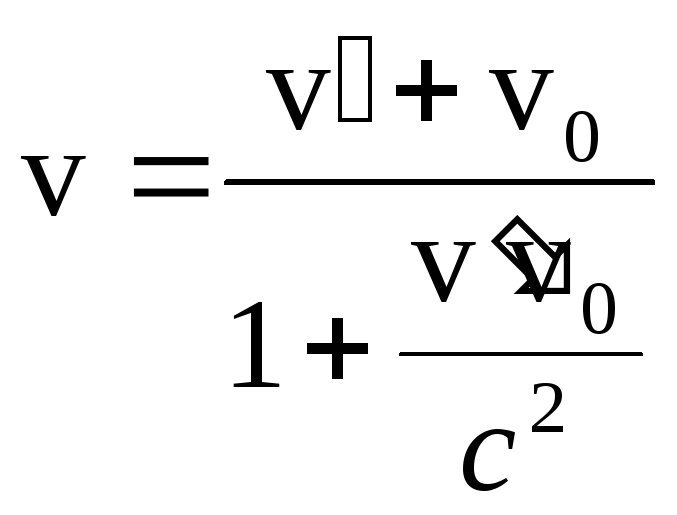 ;
;
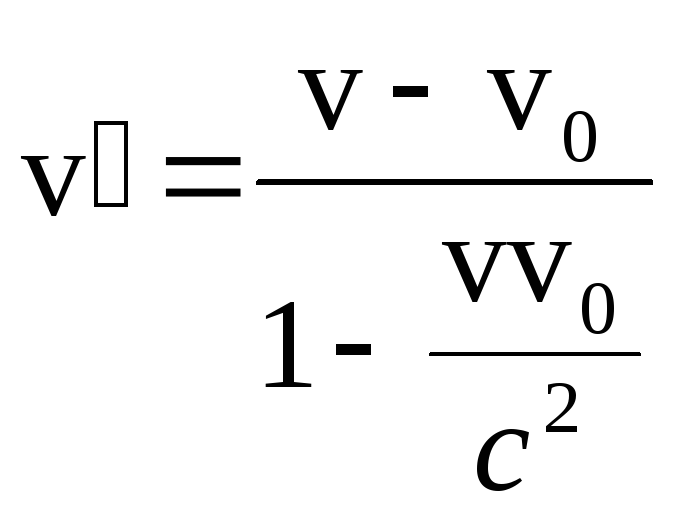 – релятивистский
закон сложения скоростей;
– релятивистский
закон сложения скоростей;
![]() ;
;
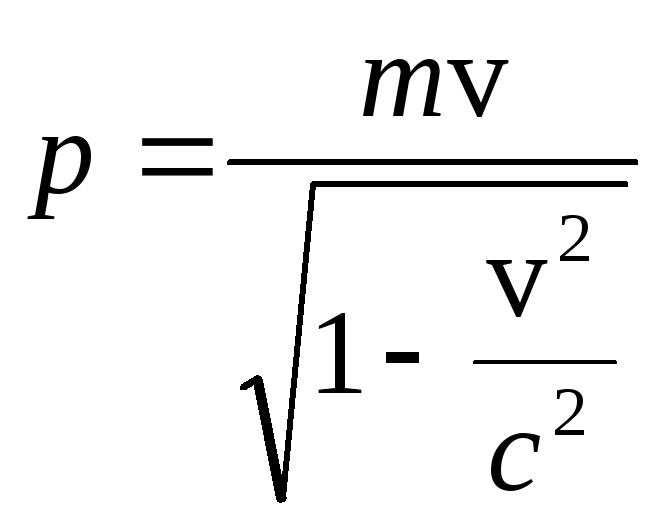 – релятивистский
импульс;
– релятивистский
импульс;
![]() –закон
динамики в теории относительности.
–закон
динамики в теории относительности.
Примеры решения задач.
Задача 10.
Импульс релятивистской частицы массой m равен mС. Под действием внешней силы импульс частицы увеличился в 2 раза. Во сколько раз при этом возрастет энергия частицы: 1) кинетическая; 2) полная?
|
Дано: p1=mС p2=2mС |
Решение:
Воспользуемся
формулой взаимосвязи импульса и полной
энергии:
откуда
Кинетическая
энергия равна разности полной и энергии
покоя:
И, наконец:
|
|
Найти:
| |
|
Ответ:
| |
10. Механика жидкостей и газов.
![]() – уравнение неразрывности;
– уравнение неразрывности;
![]() – давление;
– давление;
![]() – гидростатическое давление;
– гидростатическое давление;
![]() – закон Архимеда;
– закон Архимеда;
![]() – уравнение Бернулли;
– уравнение Бернулли;
![]() – сила вязкого трения между слоями
жидкости или газа;
– сила вязкого трения между слоями
жидкости или газа;
![]() – кинематическая вязкость;
– кинематическая вязкость;
![]() – число Рейнольдса;
– число Рейнольдса;
![]() – закон Стокса;
– закон Стокса;
![]() – объемный расход;
– объемный расход;
![]() – формула Пуазейля.
– формула Пуазейля.
Примеры решения задач.
Задача 11.
В трубе с внутренним диаметром 3 см течет вода. Определить максимальный массовый расход воды при ламинарном течении. Вязкость воды 0.001 Па.с. Ламинарность движения жидкости сохраняется при числе Рейнольдса
|
Дано: d=3 см η=0.001 Па.с Reкр.=3000 |
Решение: Массовый расход жидкости – это, аналогично объемному расходу, масса жидкости, протекающей через сечение трубы за единицу времени:
Так как m=ρV, то
Считаем течение ламинарным вплоть до критического числа Рейнольдса, тогда
где кинематическая вязкость связана с динамической:
а средняя скорость движения жидкости v позволит найти путь, пройденный частицами воды за время dt: dl=vdt и объем протекшей через поперечное сечение S за это время жидкости: dV=Sdl=Svdt. (4) Решая систему уравнений (1-4), получим:
Наконец, выразим площадь сечения трубы через диаметр:
тогда:
|
|
Найти: Qm=? | |
|
Ответ: Qm=0.071 кг/с | |
