Лабораторные работы / лаба3

СИНТЕЗ СИСТЕМЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ МЕТОДОМ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ

Цель проведения лабораторной работы

Изучение методов и приобретение навыков синтеза и моделирования системы оптимального управления в условиях известного вектора состояния.

1п.

Схема ЭДПТ как ОУ

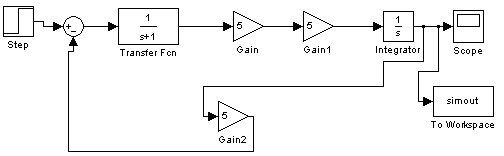
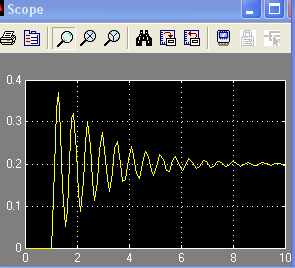
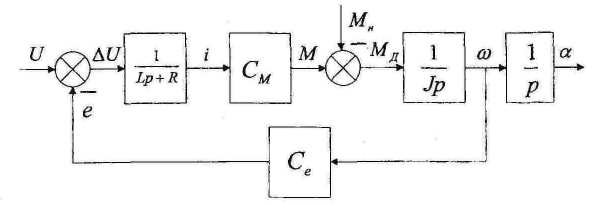
Структурная схема ЭДПТ

L = 1,102 мГн

R = 0,144 Ом

I = 0,049 кг*м²

C_e = 0,812

2п

В пространстве состояний

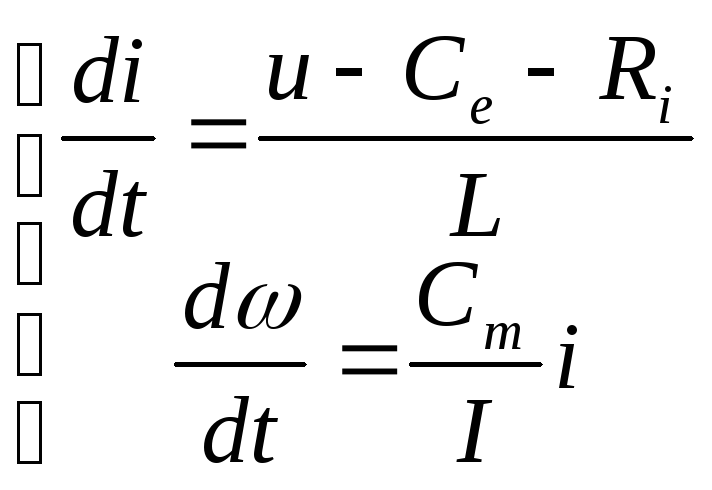
x₁ = i x₂ =

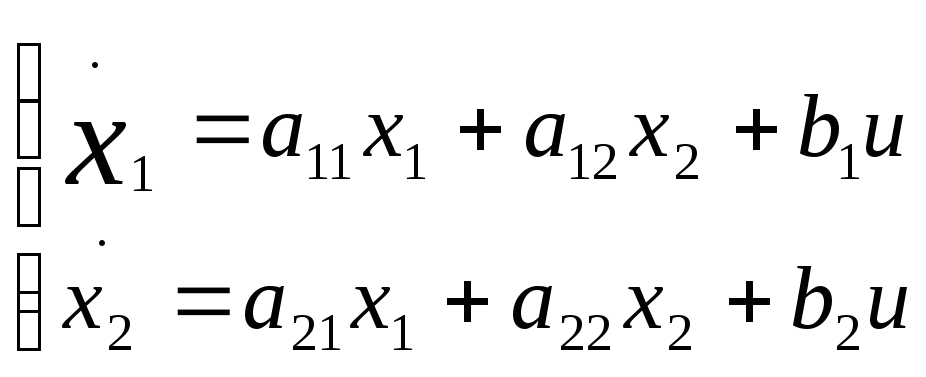
a₁₁ = - R/L a₁₂ = - C_e/L b₁ = 1/L

a₂₁= C_m/I a₂₂ = 0 b₂ = 0

Матрица поведения

3п.

ОУ в базисе интеграла

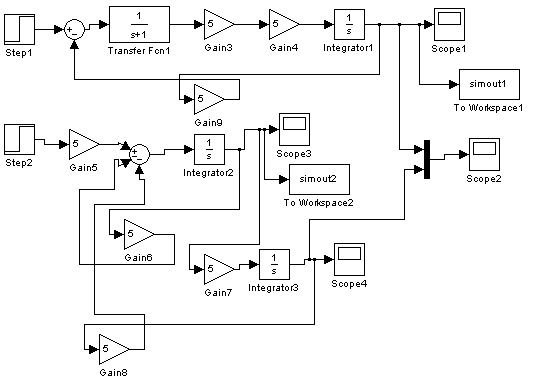
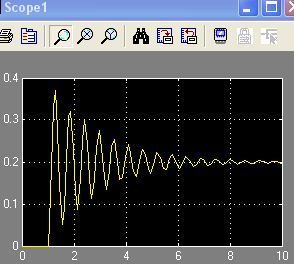
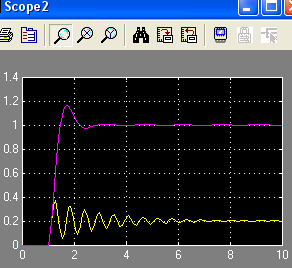
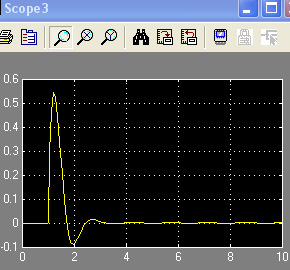
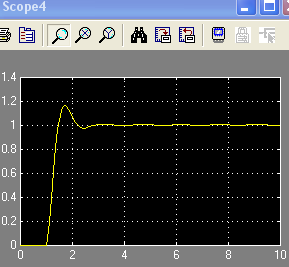
4п.

Постановка задачи оптимального управления

ОУ:

= -130,67x₁ - 736,84x₂ + 907,44u

= 16,57x₁

Критерий качества:

Синтез линейного квадратичного регулятора

Функционал качества имеет вид:

R = 1

u^* = - Gx

Решение находится из уравнения Риккати:

>> A=[-130.67 -736.84; 16.57 0]

A =

-130.6700 -736.8400

16.5700 0

>> B=[907.44; 0]

B =

907.4400

0

>> Q=[1 0; 0 1]

Q =

1 0

0 1

>> [P,L,G]=care(A,B,Q)

P =

0.0010 0.0005

0.0005 0.0722

L =

-903.1297

-21.4466

G =

0.8749 0.4762

Отсюда общая структура оптимального закона управления:

u^* = - 0,8749x₁ – 0,4762x₂

Выводы. В данной лабораторной работе изучили методы и приобрели навыки синтеза и моделирования системы оптимального управления в условиях известного вектора состояния.