Стендовая реализация лабораторной работы.

Контрольные вопросы.

1. Особенности и основные функции алгебры логики.

2. Чем комбинационная логика отличается от последовательной?

3. Назвать основные этапы построения комбинационной схемы для заданной логической функции.

4. Доказать тождество: (предлагается по выбору преподавателя)

5. Объяснить принцип использо-вания таблицы Карно для упрощения логической функции и её преимущества.

6.Приведите различные схемотехни-ческие способы реализации операций И, ИЛИ, НЕ.

Приложение 1.

Краткое техническое описание стенда.

Стенд №3

Предполагаемый внешний вид:

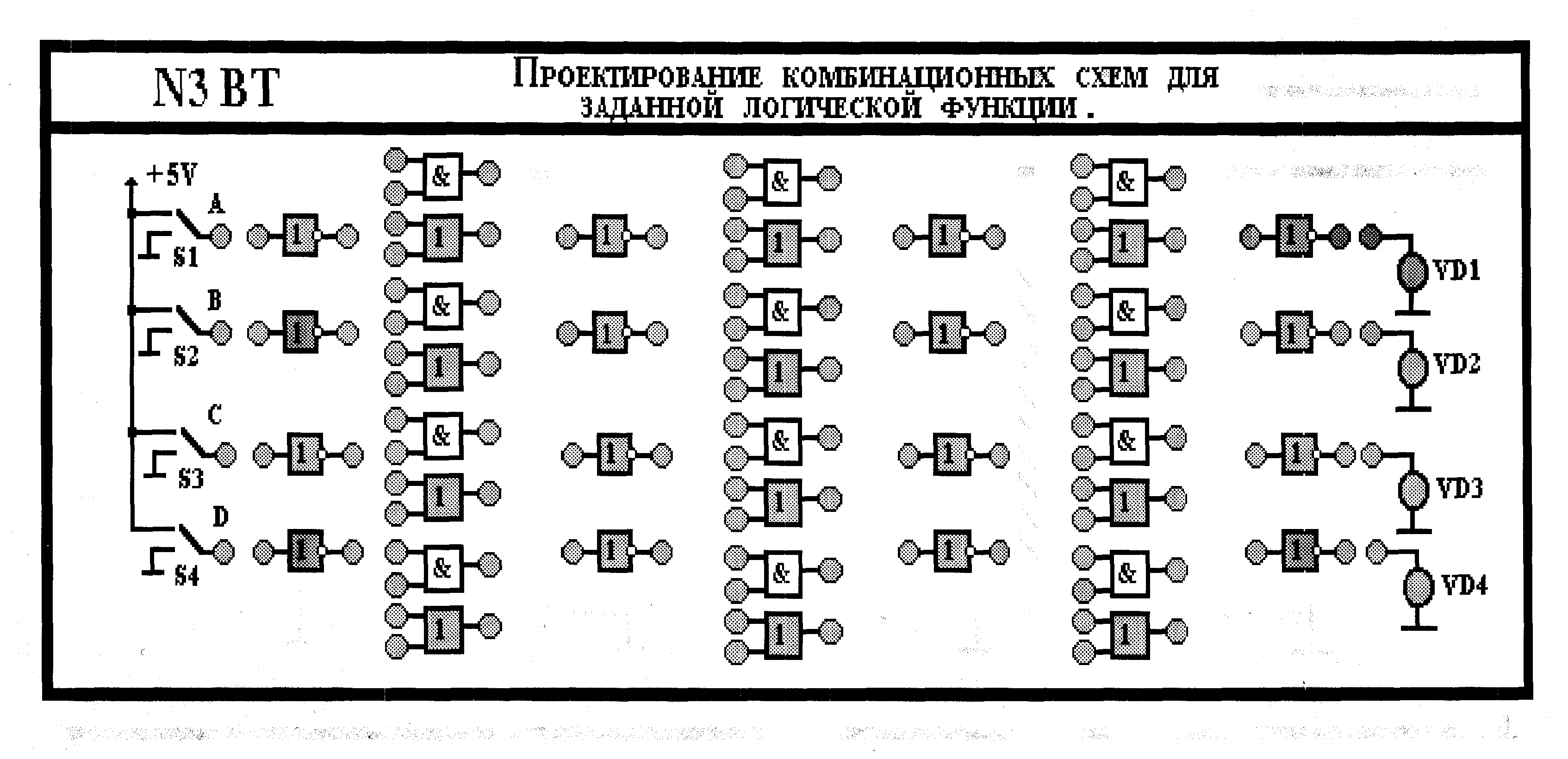
Внешний вид установки:

Исследуемые схемы монтируются на печатных платах из фольгированного стеклотекстолита, которые укрепляются на алюминиевой (дюралюминиевой) основе размером 430 на 200 мм, закрытой сверху прозрачным пластиком.

Цветное изображение исследуемых схем, название работы, переключатели находится между металлической основой и защитным пластиком. Питание стендов осуществляется от имеющихся источников, встроенных в лабораторные столы.

Приложение 2.

Виртуальная реализация лабораторной работы.

Шаг 1

Н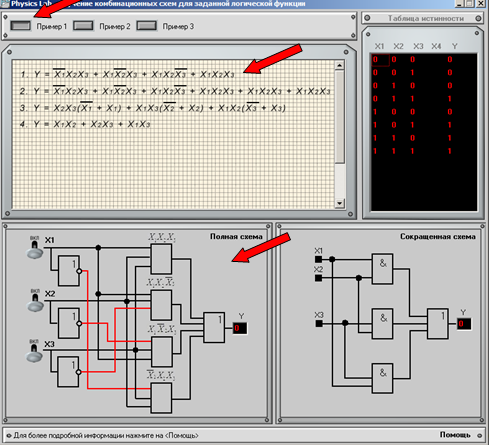 еобходимо выбрать номер примера, который необходимо рассмотреть. Затем в окне ниже можно наблюдать упрощение данного примера до более простой формы представления. В окне полная и сокращенная схема соответственно представлены данные логические схемы.

Ш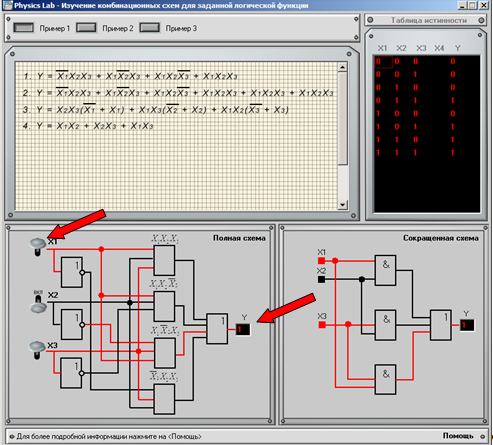 аг 2

Подавая напряжение на соответствующие входы схемы (с помощью включателей), можно наблюдать, как проходят импульсы внутри логической схемы, и просмотреть результат.

Шаг 3

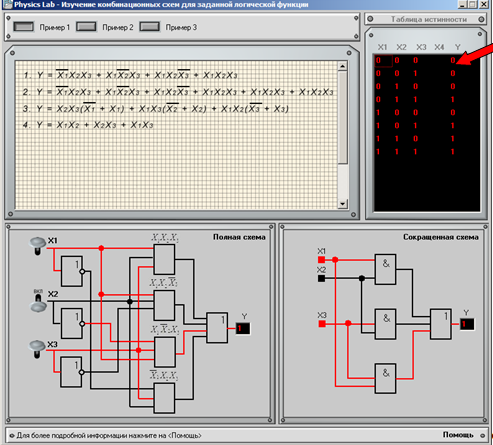Полученный результат можно сравнить с представленной таблицей истинности данной схемы.

Исследование работы шифратора и дешифратора

Цель лабораторной работы:

1) подавая на вход дешифратора двоичный код (напряжение питания либо 0 В (логический 0), либо +5 В (логическая 1) в различных комбинациях (0000, 0001, …)), установить номер загоревшего (индикатора) светодиода на выходе;

2) замыкая соответствующий номер выключателя у шифратора (от 0 до 9), установить зависимость между номером выключателя и номером индикатора (загоревшегося светодиода).

Методическая цель работы:

1. Ознакомился с принципами работы дешифраторов и шифраторов.

2. Исследовал влияние управляющих сигналов на работу дешифраторов и шифраторов.

3. Изучил реализацию и исследовал функциональные модули на основе дешифраторов и шифраторов.

Теоретическое введение.

Элементы ЭВМ выполняют функции простейших преобразований информации. Они реализуют различные логические операции над сигналами входных двоичных переменных, а также обеспечивают запоминание, формирование этих сигналов.

Функционально взаимодействующие группы таких элементов образуют различные узлы ЭВМ, которые оперируют с многоразрядными двоичными кодами, например машинными словами или их частями. К числу типовых узлов ЭВМ относятся: регистры, обеспечивающие хранение и некоторые преобразования многоразряд-ных кодов; счетчики, предназначенные для подсчета числа входных двоичных сигналов; дешифраторы, преобра-зующие входной многоразрядный код в сигнал на одном из выходов; мультиплексоры, осуществляющие передачу сигналов с одной из входных линий в выходную; сумматоры, выполняющие арифметическое суммирование двоичных кодов.

Элементы и узлы являются основой для построения других, более сложных технических устройств ЭВМ. Одним из основных узлов систем автоматического управления и вычислительной техники, а также систем связи являются дешифраторы. В современных телефонных и телеграфных системах коммутации, например, эти узлы составляют большую часть управляющего оборудования.

Слово "дешифратор" происходит от французского слова gechiffrer, что означает разгадывать, дешифровать. В научно-технической отечественной и зарубежной литературе дешифратором называют устройство преобразования принимаемых сигналов в код воспринимающей системы.

Преобразование информации в ЭВМ производится электронными устройствами (логическими схемами) двух классов: комбинационными схемами и цифровыми автоматами.

В комбинационных схемах (КС) совокупность выходных сигналов в любой момент времени однозначно определяется входными сигналами, поступающими на входы в тот же момент времени.

Реализуемый в этих схемах способ обработки информации называется комбинированным, так как результат обработки информации зависит только от комбинации входных сигналов и вырабатывается сразу при подаче входной информации.

Закон функционирования КС определен, если задано соответствие между ее входными и выходными словами, например, в виде таблицы. Это соответствие может быть задано и в аналитической форме с использованием булевых функций.

Другой, более сложный класс преобразований дискретной информации составляют цифровые автоматы. Цифровые автоматы в отличие от комбинационной схемы имеет некоторое конечное число различных внутренних состояний.

Под воздействием входного слова цифровой автомат переходит из одного состояния в другое и выдает выходное слово. Выходное слово на выходе цифрового автомата в такте определяется в общем случае входным словом, поступившим в этот такт на вход автомата, и внутренним состоянием автомата, которое явилось результатом воздействием на автомат входных слов в предыдущем такте.

Цифровой автомат содержит память, состоящую из запоминающих элементов (ЗЭ)-триггеров, элементов задержки и других элементов, фиксирующих состояние, в котором он находится. Комбинационная схема не содержит ЗЭ. Поэтому ее называют автоматом без памяти или примитивным автоматом.

Дешифраторы относятся к устройствам, изучаемым в теории комбинационных схем.

	Выходы			Выход
номера наборов	3	2	1	0	1	2	3	4	5	6	7
0	0	0	0	1	0	0	0	0	0	0	0
1	0	0	1	0	1	0	0	0	0	0	0
2	0	1	0	0	0	1	0	0	0	0	0
3	0	1	1	0	0	0	1	0	0	0	0
4	1	0	0	0	0	0	0	1	0	0	0
5	1	0	1	0	0	0	0	0	1	0	0
6	1	1	0	0	0	0	0	0	0	1	0
7	1	1	1	0	0	0	0	0	0	0	1

Таблица1.

Дешифратором называется комбинационная схема (устройство) с несколькими входами и выходами, преобразующая код, подаваемый на входы, в сигнал на одном из выходов. Если на входы дешифратора подаются двоичные переменные, то на одном из выходов дешифратора вырабатывается сигнал 1, а на остальных выходах сохраняются сигналы 0. Такой код называется унитарным, поэтому дешифратор это преобразователь двоичного кода в унитарный. Дешифраторы применяются в ЭВМ для расшифровки адресов ячеек запоминающих устройств, высвечивания букв и цифр в дисплеях, индикаторах и т. п. устройствах. Дешифраторы устанавливаются на выходах регистров или счетчиков на выходах и служат для преобразования кода слова, находящегося в регистре (в счетчике), в управляющий сигнал на одном из выходов дешифратора. В общем случае дешифратор имеет п входов и т выходов. Из подаваемой на его входы комбинации сигналов (или сигнала) в соответствии со структурой дешифратора выделяется сообщение в виде выходных сигналов дешифратора. Эти сигналы появляются на одном из выходов дешифратора и являются управляющими для объектов, подключенных к этим выходам.

Сигналы, принимаемые дешифратором могут быть звуковыми, световыми и др., однако основное применение в техники нашли электрические сигналы. Возможное количество чисел, закодированных n- разрядным двоичным кодом, равно количеству наборов из п аргументов. (р=2ⁿ), значит наибольшее число выходов дешифратора равно 2ⁿ. Такой дешифратор называется полным. Если число выходов S < р, дешифратор называют неполным, так как (p-S) наборов являются запрещенными. Переключательные функции помимо дешифратора имеют следующий вид:

;

(1)

………

Y_n-1=X_n-1X_n-2…X₁X₀;

По способу организации преобразования входного кода дешифраторы подразделяются на линейные (матричные), пирамидальные, прямоугольные и каскадные (двухкаскадные и многокаскадные).

Схема дешифратора выполняется на диодах, феррит- транзисторных ячейках, ферритовых сердечниках. Наибольшее распространение получили диодные дешифраторы. Матричные или линейные дешифраторы являются одноступенчатыми.

Проиллюстрируем синтез дешифраторов на примере полного дешифратора трехразрядных чисел. Таблица истинности дешифратора представляет собой ряд единиц, расположенных по диагонали таблицы, в остальных клетках которой стоят нули.

Таблица 1

Так как трехразрядный дешифратор имеет 2³ =8 выходов, его работа описывается восемью логическими функциями. Составленные по единицам, они имеют вид:

(2)

В случае же, когда входные сигналы поступают в однофазном коде, они предварительно преобразуются парафаз-ные внутри самого дешифратора. Подобное преобразование может быть сделано с помощью инверторов или, например, с помощью схем И, И-НЕ рис. 1"в" с запараллеленными входами. Часто дешифраторы выполняются с

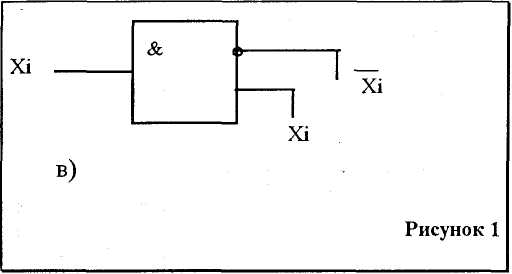
управляемой синхронизацией, при которой дешифрация кода будет произведена во время подачи синхроимпульса, поступившего на вход С, лишь при условии, что на вход (кодом управляющий (разрешающий) единичный сигнал (рис. 1г). Для реализации такого условия на дополнительные четвертые для схемы рис. 1"а" входы всех конъюнкторов подается сигнал со схемы И, на входы которой поступают сигналы С и V.

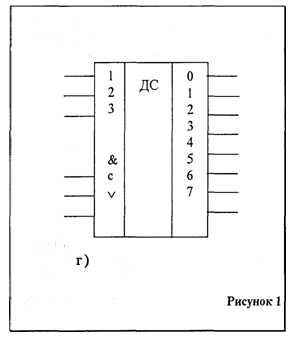
Расположенные на одной вертикальной линии конъюнкции, реализующие функции (2), дали такому дешифратору название ЛИНЕЙНЫЙ.

Достоинство линейных дешифраторов — их высокое быстродействие. Для дешифратора с парафазными входами оно определяется лишь временем задержки того единственного конъюнктора,

которыйвыдает единичный сигнал, соответствующий набору, поступившему на вход дешифратору.

Таблица 2.

Входы				Выходы
1	2	4	8	0	1	2	3	4	5	6	7	8	9
0	0	0	0	1	0	0	0	0	0	0	0	0	0
1	0	0	0	0	1	0	0	0	0	0	0	0	0
0	1	0	0	0	0	1	0	0	0	0	0	0	0
1	1	0	0	0	0	0	1	0	0	0	0	0	0
0	0	1	0	0	0	0	0	1	0	0	0	0	0
1	0	1	0	0	0	0	0	0	1	0	0	0	0
0	1	1	0	0	0	0	0	0	0	1	0	0	0
1	1	1	0	0	0	0	0	0	0	0	1	0	0
0	0	0	1	0	0	0	0	0	0	0	0	1	0
1	0	0	1	0	0	0	0	0	0	0	0	0	1

Наряду с рассмотренными видом дешифраторов применяются дешифра-торы с инверсными выходами, построенные на элементах И-НЕ.

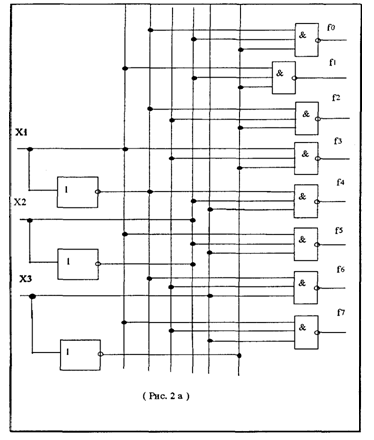
В отличие от рассмотренного на рис.1 такие дешифраторы на выходе, соответствующем поступившему на его вход набору, выдают не

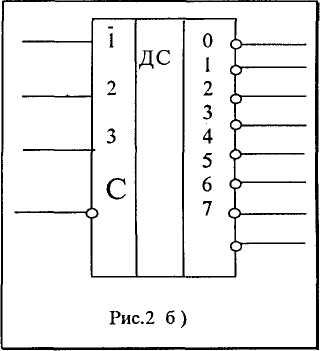
единичный, а нулевой сигнал при единичных сигналах на остальных выходах. Если при этом синхроимпульс подается на элемент И-НЕ через инвертор (рис. 2, а), то такой дешифратор с инверсными выходами и инверсным входом синхронизации обозначается, как на рис. 26) и работает лишь при С=0. Если же С=1, то все выходы данного дешифратора будут иметь единичные значение

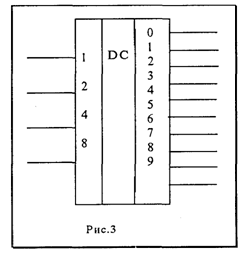
(блокированы). В интегральном исполнении матричные (линейные) дешифраторы строят на 3-4 входах. На рис.3 приведено условно-графическое обозначение матричного четырехразряд-ного дешифратора.

В таблице 2 его таблица истинности.

Переключательные функции, описывающие работу такого дешифратора, имеют следующий вид:

(3)

Входного слова осуществляется синхронизирующими сигналами С1 и С2. Такие дешифраторы принято называть синхронными дешифраторами.

Прямоугольные дешифраторы.

В таких дешифраторах осуществляется ступенчатая дешифрация. При этом дешифрируемое слово разбивается на группы разрядов и каждая из групп вначале дешифрируется матричным дешифратором. На второй ступени дешифратора, которая может быть конечной или промежуточной, образуется произведение сигналов, поступающих из первой ступени.

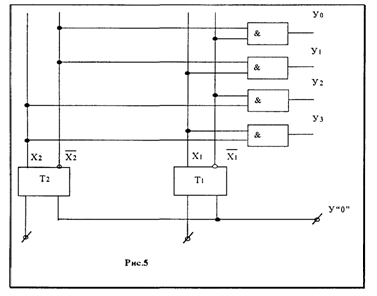
На рисунке 4 приведена схема прямоугольного дешифратора на два входа и четыре выхода. Число, представленное в двоичном коде, записывается в двухразрядном режиме (триггеры Т1 и Т2).

С единичных выходов триггеров снимаются сигналы Х1, Х2, представляющие прямые значения переменных, а с нулевых выходов триггеров снимаются сигналы, представляющие собой инверсные

значения Х1, Х2. Таким образом, с резисторов в схему дешифрации поступает парафазный код. Принцип работы рассмотренного дешифратора можно представить в виде таблицы 3:

Таблица 3.

Х2	Х1	Y0	Y1	Y2	Y3
0	0	1	0	0	0
0	1	0	1	0	0
1	0	0	0	1	0
1	1	0	0	0	1

По данным таблицы можно записать выражения для переключательных функций:

Y₀=Х₂Х₁; Y₂ = Х₂Х₁Y₁=Х₂Х₁;Y₃ = Х₂Х₁(4)

Матрица прямоугольного дешифратора в общем случае составляется из 2п вертикальных шин. Прямоугольные дешифраторы целесообразно использовать для небольшого числа дешифрируемых величин, так как при большом количестве схем совпадения число диодов резко возрастает и тогда характеристики прямоугольного дешифратора ухудшаются. В этом случае целесообразно применять ступенчатые дешифраторы.

С точки зрения оборудования многоступенчатые дешифраторы являются наиболее экономичными. Они могут быть построены в виде последовательно соединенных двухступенчатых дешифраторов.

Принцип построения многосту-пенчатого дешифратора заключается в том, что дешифрируемое слово разбивается на две группы. Затем каждая из этих двух групп разбивается также на две группы и так до тех пор, пока в каждой группе остается не более трех или двух переменных.

Структурная схема многоступен-чатого дешифратора на 10 входов приведена на рис. 6.

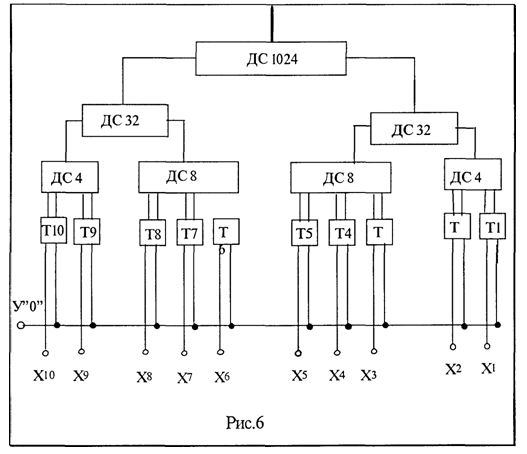
На схеме диодные матрицы изображены в виде квадратов с числом, показывающим количество выходных шин матрицы. Первую ступень дешифратора составляют четыре диодные матрицы с двумя или тремя входами и соответственно с четырьмя или восемью выходами.

Вторую ступень дешифратора составляют две матриц, каждая из которых имеет 32 выхода.

Третья ступень дешифратора содержит одну матрицу на 1024 выхода.

При построении диодных дешифраторов основным фактором в выборе схемы является экономия диодов. Поэтому наибольшее

распространение получили многоступенчатые дешифраторы.

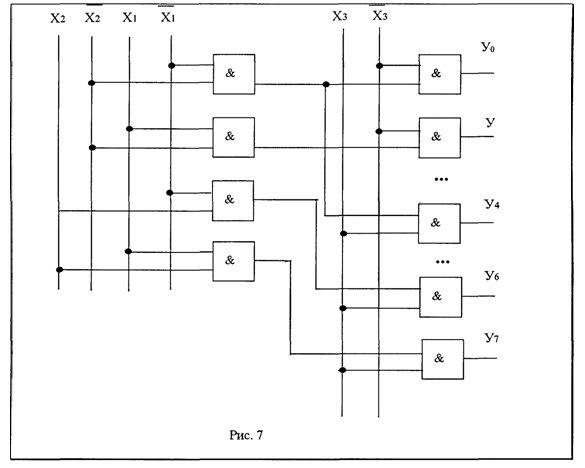
Пирамидальные дешифраторы. Пирамидальный дешифратор состоит из нескольких ступеней дешифрируемых слов. На рис. 7 изображена схема пирамидального дешифратора: предполагается, что входные переменные Х₃, X₂ X₁ поступают на него в прямой и инверсной формах, благодаря нему схема дешифратора не содержит инвенторов. В рассматриваемом дешифраторе конъюнкции входных переменных образуются постепенно. Вначале создаются всевозможные конъюнкции двух переменных X₂ Х₁ затем - конъюнкции каждого из этих произведений и третьей переменной Х₃, взятой в прямой и инверсной формах, и т. д. Из принципа построения пирамидального дешифратора следует, что в нём используются двухвходовые конъюнкторы. Количество их на входе дешифратора равно четырем, следующее "сечение" имеет 8 конъюнкторов, а число их на выходе дешифратора в общем случае равно 2n.

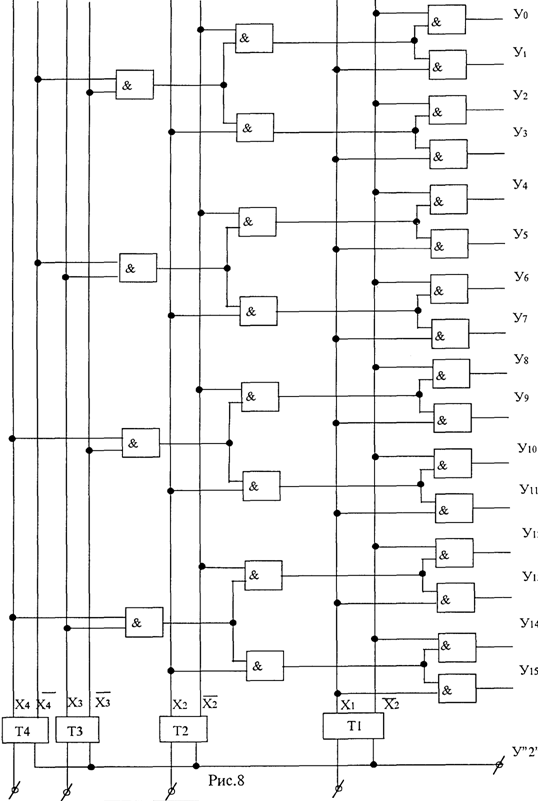
На рис. 8 приведена структурная схема пирамидального дешифратора на четыре входа. Этот дешифратор реализует систему переключательных функций. Каждый из 16 сигналов У-, формируется в три ступени. Первая ступень составлена из четырех схем совпадений, на которых поступают сигналы Х₃,Х₄ и их инверсные значения , . На выходе схем совпадения первой ступени возникают четыре сигнала представляющие собой сочетание

;Х₃ ; Х₄;Х₃Х₄;.

Вторая ступень составлена из восьми схем совпадения И. Эта ступень принимает сигналыХ₂ и Х₂от триггера Т₂ и выходные сигналы от первой ступени схем совпадения. Третья ступень составлена из шестнадцати схем совпадения, каждая из которых рассчитана на два входа. Эта ступень принимает сигналы

X₁ u от триггера T₁ и выходные сигналы схем совпадения И второй ступени. На выходе схем совпадения третьей ступени формируются выходные сигналы схемы дешифратора У₀, У_1,… У₁₅.

Пирамидальные дешифраторы в настоящее время практически не применяются, так как они строятся на двухвходовых элементах И и имеют вследствие этого громоздкую структуру и низкое быстродействие.

Шифратор ("coder") - это комбинационное устройство, выполняющее функции, обратные дешифратору. То есть преобразующий унитарный код в некоторый позиционный код. Если выходной код является двоичным порционным, то шифратор называется двоичным.

Шифраторы применяются в устройствах, преобразующих один вид кода в другой. При этом вначале дешифрируется каждая комбинация исходного кода, в результате чего на соответствующем выходе дешифратора появляется логическая 1. Затем этот логический сигнал, значение которого определено номером выхода дешифратора, подается на шифратор и на его выходах устанавливается преобразованный код.

Примером использования шифраторов являются также устройства ввода двоичных кодов в цифровое устройство с клавиатуры.

При нажатии клавиши на определенной входной шине шифратора появляется логическая 1 (шина возбуждается) и на выходах устанавливается двоичный код, соответствующий нанесенному на клавише знаку (букве, цифре и т. д)

Если число входов шифратора равно 2", то число выходов, очевидно, должно быть равно п, т.е. числу разрядов двоичного кода, которым можно закодировать 2ⁿ ситуаций.

Проиллюстрируем синтез схемы шифратора при n=3. Таблица истинности (4) имеет вид:

Таблица 4

Входы	Выходы
X	YЗ	Y2	Y1
0	0	0	0
1	0	0	1
2	0	1	0
3	0	1	1
4	1	0	0
5	1	0	1
6	1	1	0
7	1	1	1

Переключательные функции, описывающие работу этого шифратора, имеют вид:

Y₃=Y₄vX₅vX₆vX₇; Y₂=Y₂VX₃VX₆VX₇;

Y₁=Y₁VX₃VX₅VX₇;

Три функции (5) реализуются тремя дизъюнкторами, на выходах которых формируется трехразрядный двоичный код. (рис 9)

Десятичный код	Двоичный код 8-4-2-1
X	Y3	Y2	Y1	Y0
0	0	0	0	0
1	0	0	0	1
2	0	0	1	0
3	0	0	1	1
4	0	1	0	0
5	0	1	0	1
6	0	1	1	0
7	0	1	1	1
8	1	0	0	0
9	1	0	0	1

Так как аргумент Х₀ не входит ни в одну из логических функций (5), шина Х₀ остается незадействованной. Это означает, что при единичном сигнале на входе Х₀ на выходе шифратора окажется нулевой набор. Такой же нулевой набор будет на выходе и при отсутствии единичного сигнала на входе Х₀. Таким образом, строго говоря шифратор реагирует на 2^n-1входов.

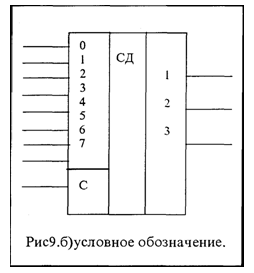
Кроме шифраторов с прямыми входами и выходами (рис. 9) применяются шифраторы с инверсными входами и выходами (рис.10)

Как правило, и те и другие выполняются синхронными (входы С на рис. 9б и 10)

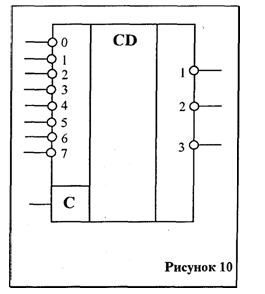
Рассмотренный шифратор — линейный, его недостаток — большое число входов (2^n-1) у каждого дизъюнктора, резко возрастающее с увеличением n. Для реализации шифратором с большим n используется принцип каскадного соединения.

Рассмотрим принцип построения 10-входного двоичного дешифратора, закон функционирования которого задан таблицей истинности 5:

Назначение такого дешифратора — преобразовать входной код, изображающий десятичную цифру 0,1,2,...,9 логической 1 на соответствующем входе в двоичный код. На основе таблицы 5, переключательные функции, описывающие работу шифратора, имеют вид:

Y₀=X₁vX₃vX₅vX₇vX₉;

Y₁=X₂vX₃vX₆vX₇;

Y₂=X₄VX₅VX₆VX₇;

Y₃=X₈VX₉;

На рис. 11 а, б приведены функциональная схема шифратора на 10 входов, реализующая эти выражения, и его условное обозначение:

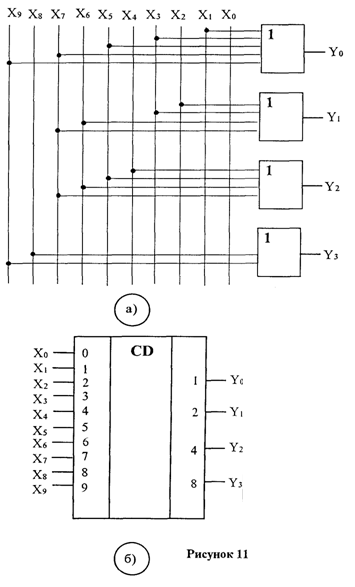
С помощью шифраторов возможно преобразование цифр десятичных чисел в двоичное представление с использованием любого другого двоично-десятичного кода.

Методика исследования.

Работа шифратора и дешифратора.