Стендовая реализация лабораторной работы.

Контрольные вопросы.

Какие существуют основные логические операции?

Составить таблицы истинности этих операций.

Каковы условные обозначения логических элементов И, ИЛИ, НЕ, реализованных на диодах (ДРЛ).

Объясните принцип действия логических элементов И, ИЛИ, НЕ, реализованных на транзисторах (ТТЛ).

6. Охарактеризуйте работу элемента НЕ в статическом и динамическом режимах.

Принципиальная схема лабораторной работы № 2. Краткое описание ее работы.

Данное устройство собрано на трех микросхемах:

К555 ЛИ1 включает в себя 4 двухвыводных элемента &(И)

К555 ЛЛ1 включает в себя 4 двухвыводных элемента 1(ИЛИ)

К555 ЛН1 включает в себя 6 одновходовых элементов НЕ переключатели типа П2к и ПКН 41-1-2;

светодиоды для индикации входных и выходных переменных (8 штук).гнезда 64, 04 (4 штуки).

Приложение 1.

Краткое техническое описание стенда.

Стенд №2

Предполагаемый внешний вид:

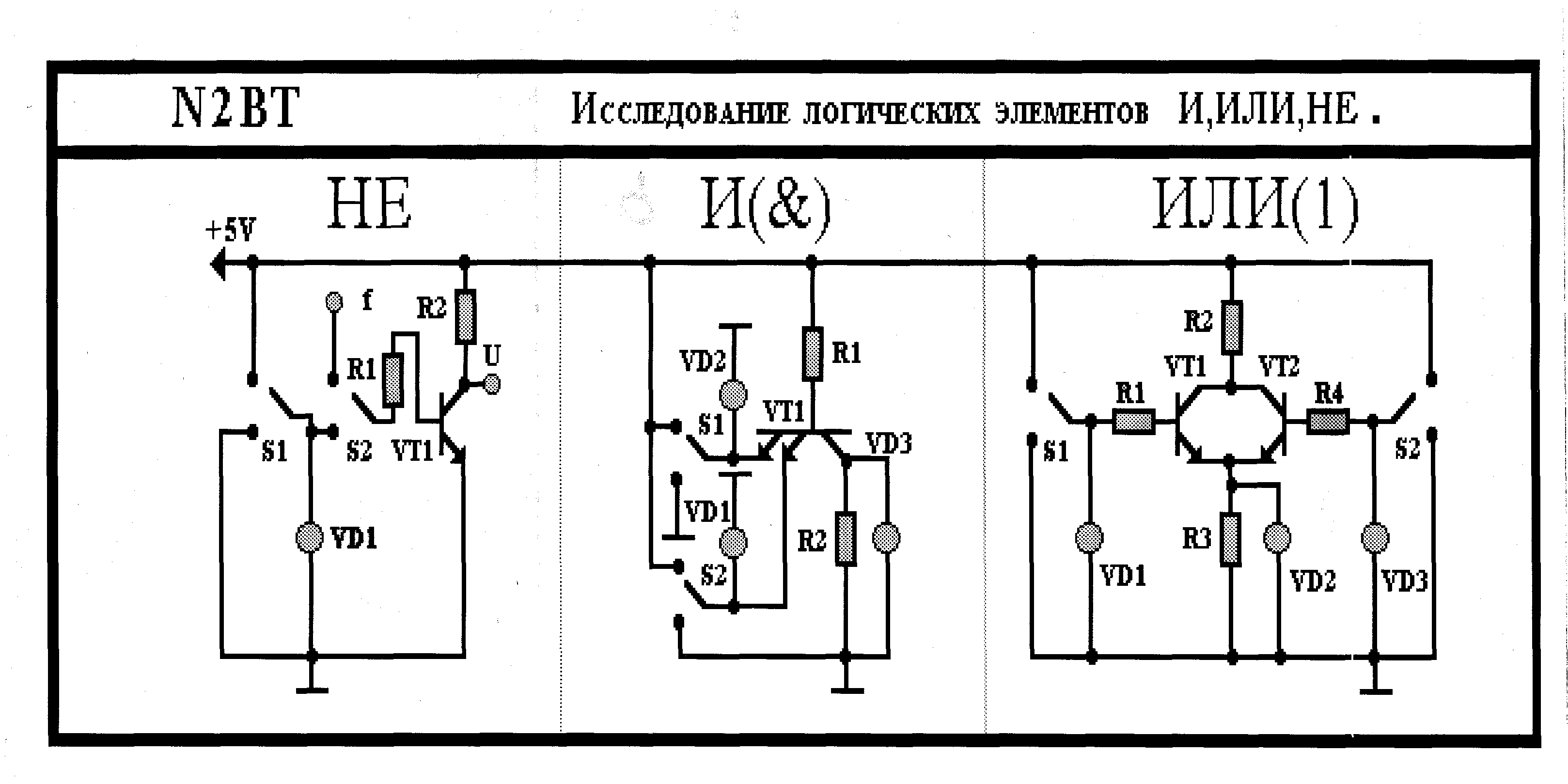
Внешний вид установки:

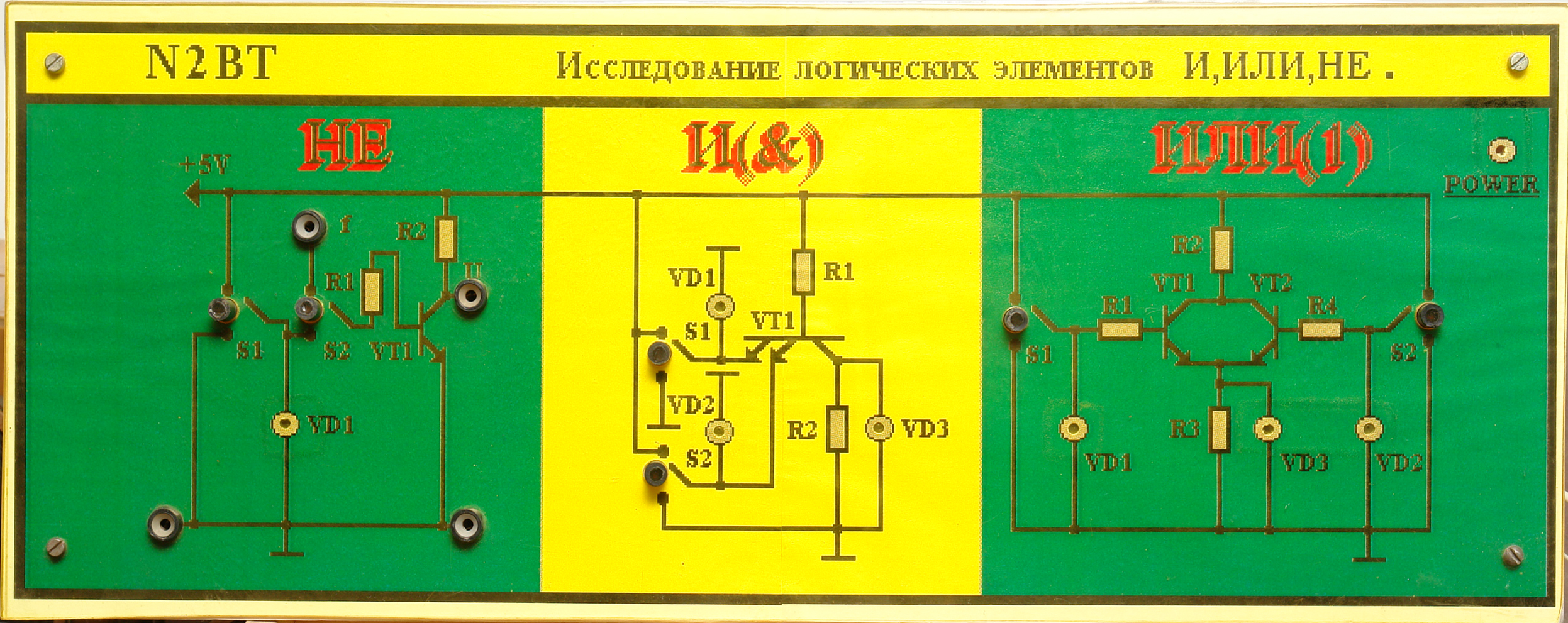
Исследуемые схемы монтируются на печатных платах из фольгированного стеклотекстолита, которые укрепляются на алюминиевой (дюралюминиевой) основе размером 430 на 200 мм, закрытой сверху прозрачным пластиком.

Цветное изображение исследуемых схем, название работы, переключатели находится между металлической основой и защитным пластиком. Питание стендов осуществляется от имеющихся источников, встроенных в лабораторные столы.

Приложение 2.

Виртуальная реализация лабораторной работы.

Шаг 1

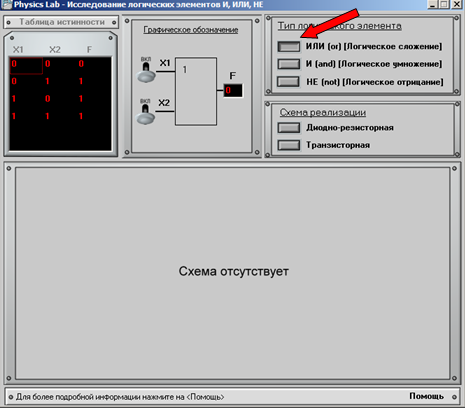
Необходимо выбрать схему реализации выбранного логического элемента, которая будет отображена в главном окне.

Шаг 2.

Необходимо выбрать тип логического элемента, принцип работы которого необходимо просмотреть.

Ш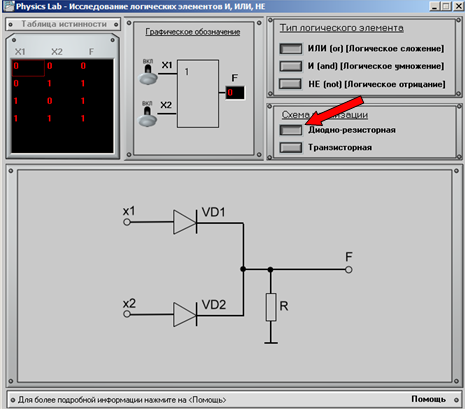 аг 3.

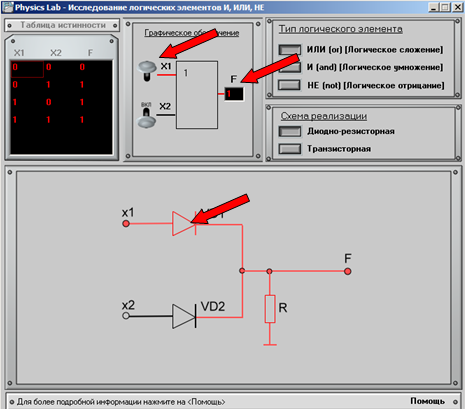
Переключая переключатели в окне «Графическое обозначение», подаем импульсы на входы логического элемента. При этом на схеме, красным цветом отображаются импульсы, проходящие внутри элемента. На выходе «F» в окне «Графическое обозначение» отображается конечный результат.

Шаг 4.

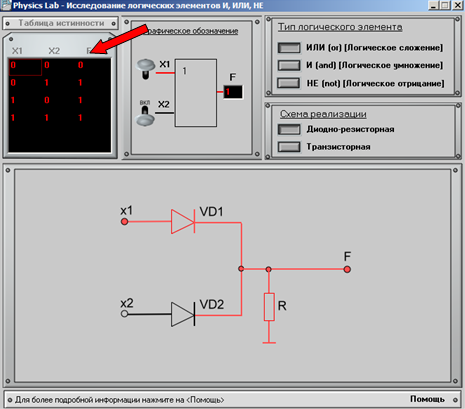
Полученные результаты сравнить с таблицей истинности данного элемента.

Проектирование комбинационных схем для заданной логической функции.

Цель лабораторной работы:

1) используя таблицы Карно (теорию графов или любой другой подходящий метод), минимизировать предложенную преподавателем таблицу истинности и с использованием схем И, ИЛИ, НЕ нарисовать электронный вариант ее реализации;

2) собрать на стенде нарисованную Вами схему;

3) подавая на вход схемы напряжения от А-D, соответствующие логическому 0 или 1, убедится в том, что ее работа соответствует заданной таблице истинности.

Теоретическое введение.

Типовые элементы логических устройств служат основой для создания цифровых вычислительных машин и автоматов дискретного действия. В логических устройствах сигнал на входе и выходе каскада является двоичным, бинарным. Он может принимать только два значения — логического нуля "0" и логической единицы "1". Значения "0" и "1" являются символическими (условными) и не соответствуют числовым значениям напряжения, выраженным в вольтах. Например, при использовании выходного напряжения ключевого каскада уровнем логического нуля "0" может служить напряжение на коллекторе насыщенного транзистора U_кн, уровнем логической "1" — напряжение на коллекторе запертого транзистора Е, В (или наоборот, в зависимости от того, какими символами предварительно условились обозначать уровни U_кн и Е). Входные сигналы логических каскадов обозначают буквами Х₁ Х₂, ..., Х_n, где n число входов логического каскада. Напряжение на каждом входе является бинарным. Выходной сигнал логических каскадов обозначается буквой Y. В общем случае логический каскад может иметь несколько выходов; если выходов, например, два — будем обозначать их буквами Р и Q.

Типовые каскады логических устройств можно разделить на два класса - соответственно логические элементы и элементы памяти. Логические элементы осуществляют преобразование логических сигналов, элементы памяти - запоминание информации. Логические устройства можно разделить на комбинационные и последовательные. Комбинационные логические устройства состоят из логических элементов, выходной сигнал зависит только от значений входных сигналов в рассматриваемый момент времени. Последовательные логические устройства кроме логических элементов содержат и элементы памяти, выходной сигнал зависит не только от значений входных сигналов в рассматриваемый момент времени, но и от напряжения на выходах элементов памяти, которое является результатом логической обработки сигналов, поступающих в предшествующие моменты времени.

Булева алгебра, основные теоремы и тождества.

В настоящее время для построения систем обработки и преобразования информации широко применяют цифровые методы. Используемые при этом сигналы близки по форме к прямоугольным, и имеют два фиксированных уровня напряжения. Уровню низкого напряжения обычно приписывается символ (состояние) "0", а уровню высокого напряжения — символ (состояние) "1".

Математическим аппаратом анализа и синтеза цифровых систем служит алгебра логики (булева алгебра), которая изучает связь между переменными (сигналами), принимающими только два ("0", "1") значения. Символ "0" и "1" в алгебре логики характеризуют состояние переменных или состояние их функций, в связи с чем, эти символы нельзя рассматривать как арифметические числа. Алгебра логики является алгеброй состояния, а не алгеброй чисел, и для неё характерны основные действия, отличные от принятых в обычной алгебре действий над числами.

В алгебре логики любая переменная может иметь состояние "0" или "1". Поэтому алгебре логики каждой двоичной переменной, например, X, ставится в соответствие обратная или дополнительная к ней (инверсная ) переменная, такая, что:

если Х=0, то ,

если Х=1, то

Существуют три основные операции между логическими переменными:

• конъюнкция (логическое умножение);

• дизъюнкция (логическое сложение);

• инверсия (логическое отрицание).

Эти операции были рассмотрены в лабораторной работе №2.

Основные теоремы алгебры Буля.

• Теоремы для одной переменной.

Эти теоремы охватывают все случаи над переменной X и

константами 0 и 1:

1)Х+0=Х 2) X+1=1

3)X+X=X 4)X+ =1

5)X•0=0 6)X•1=1

7) X•X=X 8) X• =0

9)

• Теоремы для двух и более переменных.

1 0) X₁+X₂=X₂+X₁ X₁X₂=X₂X₁

Смысл, как и в обычной алгебре закон коммутативности.

Теорема справедлива и при любом числе переменных. Результат операции ИЛИ и И не зависит от порядка написания переменных. В применении к логическим схемам это означает, что выходной сигнал элементов ИЛИ и И не зависит конечно от того, какие входные сигналы к клеммам подводятся.

1 1)

a) X₁+X₂+X₃=X₁+(X₂+X₂)=(X₁+X₂)+X₃

b) X₁X₂X₃=X₁(X₂X₃)

Закон (закон ассоциативности); также аналогичный соответствующему закону алгебры.

12) a) X₁+(X₂+X₃)=X₁X₂+X₁X₃

b) X₁+X₂X₃=(X₁+X₂)(X₁+X₃)

Распределительный закон;(Закон дистрибутивности)

Приведенные выше теоремы 10, 11, 12 так же как и все последующие даются в двух вариантах: для логического сложения и для логического умножения.

13) a) X₁+X₁X₂=X₁

b) X₁(X₁+X₂)=X₁

закон поглощения

Для доказательства теоремы 13а вынесем переменную X₁ за скобки: X₁(1+X₂)=X₁. В соответствии с теоремами 2 и 6 (1+Х₂)=1, а Х₁1=Х₁ что и доказывает справедливость теоремы.

1 4) a)(X₁+ )X₂=X_lX₂

b)

1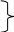 5) a)X₁X₂+ X₂=X₂

b)(X₁+X₂)( +X₂) =

Закон склеивания.

16)a)

b)

П ри любом числе переменных:

с)

d)

Теорема де Моргана.

Справедливость этой теоремы вытекает непосредственно из принципа двойственности. Пусть имеем выражение для логического произведения трех переменных в виде: F=X₁X₂X₃. В соответствии с принципом двойственности при замене всех переменных их отрицаниями и операции умножения операцией сложения получаем отрицание результата, то есть . Подставим в левую часть первоначальное значение F=X₁X₂X₃. Тогда получим

, что совпадает с теоремой 16г.

Логические функции

Логическая функция Y будет определена, если звестно ее значение для каждого возможного набора переменных X₁,X₂,…,X_n. Если же для некоторых наборов переменных значение функции У не задано, то функцию называют неопределенной или частично определенной. Бывают случаи, когда некоторые наборы переменных по условиям задачи заведомо невозможны и функция Y=f(X₁,X₂,...,X_n) недоопределена именно для этих наборов переменных. В этом случае логическую функцию можно доопределить для запрещенных наборов любыми значениями ("0" или "1") для удобства последующего анализа или представления функции. Дополнительные условия, исходя из которых доопределяют частично определенную функцию, называют факультативными условиями.

Способы представления функций.

Существуют различные способы задания или представления булевых функций.

Представление функции на словах. Например, функция трех аргументов принимает значение 1, если два любых аргумента или все три равны 1. Во всех других случаях функция равна 0. Этим функция и логика работы соответствующей схемы полностью задана.

Табличный способ. При этом способе функция представляется в виде таблицы, в которой выписываются все возможные наборы аргументов в порядке возрастания их номеров и для каждого набора устанавливается значение функции 0 или 1.

Например, в таблице 1 задана функция F.

Как видно из таблицы, функция F=1 на 3-, 5-, 6- , 7-м наборах на остальных четырех F=0. Изменяя комбинации нулей и единиц в последней колонке таблицы, можно, как это следует из предыдущего, задать 256 различных функций 3-х аргументов, хотя лишь некоторые из них имеют практический смысл.

Таблица 1.

Номер набора	A	В	C	D
0	0	0	0	0
1	0	0	1	0
2	0	1	0	0
3	0	1	1	1
4	1	0	0	0
5	1	0	1	1
6	1	1	0	1
7	1	1	1	1

Логическая схема соответствующая функции F, которая задана в таблице 1, называется мажоритарным элементом типа "2 из З". Значение выходной переменной этого элемента всегда соответствует большинству значений входных переменных.

При п аргументах совокупность всех значений полностью определенной функции на 2ⁿ наборах содержит 2ⁿ нулей и единиц. Каждой функции соответствует своя комбинация этих 2ⁿ значений. Общее количество всех возможных функций n аргументов определяется количеством комбинаций из 2ⁿ нулей и единиц, то есть количеством различных 2ⁿ разрядных двоичных чисел. Оно равно числу

N = . Величина N очень быстро растет с ростом числа аргументов. Так при n=2 — N=16, при n=3 — N=256.

Алгебраический способ. От таблицы можно перейти к алгебраической форме функции или к структурной формуле. В такой форме удобно производить различные преобразования функции, например с целью минимизации.

Существует две формы функций в алгебраическом виде называемые нормальными.

Первая форма, которая называется также дизъюнктивной нормальной функцией (ДНФ) представляет собой логическую сумму элементарных логических произведений, в каждое из которых аргумент или его отрицание входит не более одного раза. Например,

.

Если каждое слагаемое содержит все переменные или их отрицание, имеем первую стандартную форму или совершенно дизъюнктивную нормальную форму (СДНФ). Например,

Вторая форма или конъюнктивная нормальная форма (КНФ) — есть логическое произведение элементарных логических сумм. Когда каждая сумма содержит все переменные или их отрицание, имеем вторую стандартную форму или совершенную конъюнктивную нормальную форму (СКНФ). Например,

записана во второй стандартной форме.

От табличной формы представления логической функции нетрудно перейти к аналитической форме ее записи. Например, из таблицы 2 видно, что значение функции истинно только для некоторых наборов переменных. Значение Y равно единице, если:

а) X₁=0, X₂=1, Х₃=1

(для сочетания Х₂Х₃);

б) X₁=1, X₂=0, Х₃=1

(для сочетанияХ₁ Х₃ );

в) X₁=1, X₂=1, Х₃=0

(для сочетания Х₁Х₂ );

г) Х₁=7, Х₂=1, Х₃=1 (для сочетанияХ₁Х₂Х₃ );

Каждое из произведений переменных, для которых значение Y истинно, носит название минтерма. Логическую функцию можно представить в виде суммы минтермов.

.

Функция Y= f(X₁ X₂ Х₃) представлена в виде дизъюнкции произведений переменных или их отрицаний. Если при такой записи каждое слагаемое содержит произведение всех переменных X₁, X₂ ... , Х_n или их отрицаний, про такую форму представления называют совершенной дизъюнктивной нормальной формой или первой стандартной формой.

Точно так же можно выделять и неистинные (нулевые) значения функции, иллюстрирующиеся в таблице 2. В рассматриваемом случае функция Y принимает нулевые значения ( ), если:

а) X₁=0, Х₂=0, Х₃=0

(для сочетания );

б) Х₁=0, Х₂=0, Х₃=1

(для сочетания );

в) X₁=0, Х₂=1, Х₃=0

(для сочетания );

г) X₁=1, Х₂=0, Х₃=0

(для сочетания );

Следовательно,

откуда, используя принцип двойственности или правило де Моргана, получим

Функция Y дана в виде произведения (конъюнкция) сумм переменных или их отрицаний. Такую форму представления логической функции называют совершенной конъюнктивной нормальной формой или второй стандартной формой.

С появлением сложных переключательных схем булева алгебра легла в основу теории схем, называемых логическими.

Впервые возможность применения булевой алгебры для этих целей была показана В. И. Шестаковым (1936 г.), а затем независимо от него К. Шенноном (1938 г.)

В теории логических схем логика работы элементов, узлов и устройств в целом отображается алгебраическими формулами. Это дает возможность, прежде всего, произвести анализ заданной логической схемы, то есть определить значения выходных двоичных переменных.

Другой, самой важной задачей является синтез логической схемы по заданной каким-либо образом логике ее работы. Сначала схема описывается алгебраическими формулами. Затем эти формулы преобразуются к виду, которому соответствует наиболее простая логическая схема. В большинстве случаев при этом стремятся получить схему, содержащую минимальное число элементов.

Построение комбинационной логической схемы по заданной функции.

Получив аналитическую запись логической функции Y= f(X₁,X₂...,X_n), можно осуществить переход к тому цифровому логическому устройству, которое сможет осуществить обработку поступающих логических сигналов Х₁Х₂...,Х_n по заданным требованиям.

Например, мы получим запись логической функции:

(1)

Для создания логического устройства, выполняющего логическую обработку сигналов X₁,X₂ и Х_n, в данном случае потребуется:

а) инверторы; их число, необходимое для реализации схемы, равно трем;

б) схемы И, которые обеспечивают операцию конъюнкции;

в) схемы ИЛИ на четыре входа.

Построение логической схемы выполняющей обработку сигналов согласно функции (1), отражено на рисунке 1.

Аналогичным путем можно проектировать устройства, соответствующие другим функциям.

Однако, построение комбинационных логических схем на основании булевых функций, представленных в виде первой или второй стандартных форм, как они получаются при переходе от таблиц к формулам, в большинстве случаев нецелесообразно.

Переходу к логической схеме должно предшествовать упрощение структурных формул с целью приведения их к первому виду, при котором соответствующая им схема более полно удовлетворяла бы требованиям, предъявляемым к ней. В первую очередь, стремятся в результате упрощения, получить минимальное количество логических элементов в схеме:

Таким образом, возникает необходимость минимизации булевых функций.

Основная задача минимизации состоит в получении минимальной формы булевой функции, то есть такой формы, которой соответствует логическая схема с минимальным числом элементов.

Существует множество способов минимизации булевых функций. В рамках данного курса рассматриваются два из них:

• алгебраический метод;

• метод таблиц Карно.

Минимизация булевых функций алгебраическим методом.

Типовым примером при алгебраической минимизации функций можно считать:

а) прибавление одного или нескольких однотипных членов, из числа имеющихся в первой стандартной форме. Так как А+А+...+А=А, то прибавление к имеющемуся члену А одного или нескольких таких же членов не изменит справедливости равенства У= f(X₁X₂...,X_n);

б) умножение отдельных членов функции на сумму Ал- А, где А может быть как одной из переменных Х₁Х₂,...,Х_n , так и функцией этих переменных. Поскольку + =1, то такое умножение не нарушит тождественности исходного и полученного соотношений;

в) выделение слагаемых типа + путем применения закона дистрибутивности. После представления суммы в виде двух сомножителей, один из которых имеет вид + , выражение упростится, поскольку + =1;

г) использование законов склеивания (15) и поглощения (13).

После проведения всех возможных преобразований получают функцию, не имеющую избыточных членов и не поддающуюся дальнейшей минимизации. Эту форму записи функции часто называют тупиковой. Функция может иметь несколько тупиковых форм.

В качестве примера алгебраической минимизации рассмотрим преобразование функции:

(1)

К слагаемому А=Х₁Х₂Х₃ добавим еще два таких слагаемых. Справедливость равенства (1) при этом не нарушится:

(2)

Произведем группировку членов на основании использования закона дистрибутивности (12):

(3)

Отсюда, Y=Х₁Х₂+Х₂Х₃+Х₁Х₃. Эта форма записи является тупиковой.

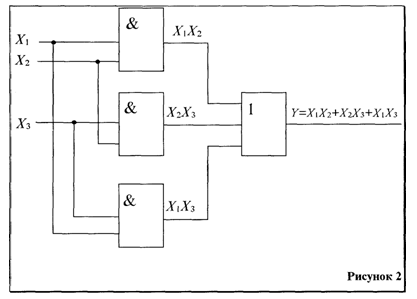
Схема логического устройства реализующая тупиковую форму представления функции, показана на рисунке 2.

Вывод: из сравнения рисунка 2 с рисунком 1 видно, что минимизация функции позволила существенно упростить устройство: отпала необходимость в инверторах, потребовалось меньшее число входов у каждого из элементов И и ИЛИ.

Дальнейшее преобразование полученной тупиковой формы зависит уже от имеющихся в наличии логических элементов конкретного типа для того, чтобы реализовать устройство на элементах одного типа.

Минимизация булевых функций с помощью карт Карно.

Минимизация функций алгебраическим методом требует определенного навыка. Далеко не всегда очевидно, что полученная форма является тупиковой; иногда трудно определить и "склеивающиеся" слагаемые.

Разработан метод минимизации как бы автоматизирующий процедуру поиска "склеивающихся" слагаемых — метод карт Карно.

Карта Карно, или диаграмма Вейча — это таблица, имеющая ячейки для всех возможных минтермов функции.

Каждое из произведений переменных для которых значение Y истинно носит название минтерма.

Например, функцию Y=f(X₁,X₂...,X_n) можно представить в виде суммы минтермов:

Можно построить карты для функций, минтермы которых содержат два, три или более переменных.

На рисунке 3 показана карта Карно для функции двух переменных. Вдоль верхней грани проставлены возможные значения переменной Х₁ вдоль левой грани — возможные значения переменной Х₂ ("0" и "1").

Карта содержит четыре клетки. В каждой клетке изображают один из возможных минтермов: , Х₁ , Х₂ или Х₁ Х₂.

Если какой-нибудь из минтермов в совершенной дизъюнктивной нормальной форме записи функции присутствует, то в соответствующей клетке карты Карно ставится "1". Иначе ставится — "0".

Таблица (или карта) Карно — это измененная запись таблицы переключений.

Значения входных переменных не просто записывается рядом друг с другом, а размещаются по горизонтали и вертикали таблицы, деля ее на отдельные квадраты.

При нечетном количестве входных переменных по горизонтали размещается на одну переменную больше чем по вертикали (или наоборот).

Порядок размещения различных комбинаций значений входных переменных следует выбрать таким, чтобы при переходе от одной ячейки к соседней изменялась лишь одна переменная.

Например, таблица истинности для функции ИЛИ и соответствующая ей таблица Карно

X1	X2	Y
0	0	0
0	1	1
1	0	1
1	1	1

	0	1
0	0	1
1	1	1

Преимуществом таблиц Карно является простота обнаружения возможных упрощений логической функции.

	00	01	11	10
0	0	0	1	0
1	0	1	1	1

Рассмотрим это на примере. Минимизируем функцию (1).

Заполненная карта Карно соответствующая этой функции показана на рисунке 5.

Общее правило упрощения логической функции для таблиц Карно заключается в следующем.

Если в двух, четырех, восьми и так далее ячейках, ограниченных прямоугольным или квадратным контуром, стоят только единицы, можно записывать непосредственно логическое произведение для всей этой группы, причем в это произведение должны входить лишь те входные переменные, которые остаются неизменными для ячеек данной группы.

Единица, изображающая минтерм Х₁Х₂,Х₃, входит сразу в три объединения обозначенными контурами а,b и с.

Объединение, соответствующее контуру а, отображает "склеивание" минтермов X₁X₂X₃ и Х₁ Х₃.

X₁X₂X₃+Х₁ Х₃ =X₁X₃(X₂+ )=X₁X₃

Объединение, отмеченное контуром Ь, отображает "склеивание" минтермов X₁X₂X₃ и Х₂Х₃.

X₁X₂X₃+ Х₂Х₃ =X₂X₃(X₁+ )=X₂X₃

Объединение, отмеченное контуром с, отображает "склеивание" минтермов X₁X₂X₃ и Х₁Х₂ .

X₁X₂X₃+Х₁Х₂ =X₁X₂(X₃+ )=X₁X₂

В результате проведенных операции "склеивания" из четырех минтермов, входящих в функцию (1) и являющихся конъюнкцией трех переменных, остались лишь слагаемые X₁X₂;X₂X₃;X₁X₃.Отсюда

Y= X₁X₂+X₂X₃+X₁X₃, что было ранее показано алгебраическим методом.

Карта Карно позволила легко выявить "склеивающиеся" минтермы и облегчила задачу минимизации функции. Естественно, что тупиковая форма записи функции, полученная при минимизации по карте Карно, используется при проектировании логических устройств также как и полученная методом алгебраической минимизации.

Для закрепления изложенного материала войдите в основное меню, и выберете там опцию «Тест 3». Выполните предлагаемые там упражнения (иллюстрация работы созданной программы (программа эксклюзивная!) приведена в приложении 1)

Методика исследования.

Проектирование комбинационных схем для заданной логической функции.