Стендовая реализация лабораторной работы.
Контрольные вопросы.
Для чего нужны счетчики?
Принцип действия суммирующего счетчика.
3. Зарисовать схему и временные диаграммы суммирующего счетчика.
4. Принцип действия вычитающего счетчика.
5. Зарисовать схему и временные диаграммы вычитающего счетчика. Какие еще бывают счетчики?
6. Их отличие от вычитающих и суммирующих счетчиков.
7. На основе экспериментальных данных доказать, что счетчик производит счет импульсов и деление частоты.
Приложение 1.
Краткое техническое описание стенда.
Стенд №8
Предполагаемый внешний вид:
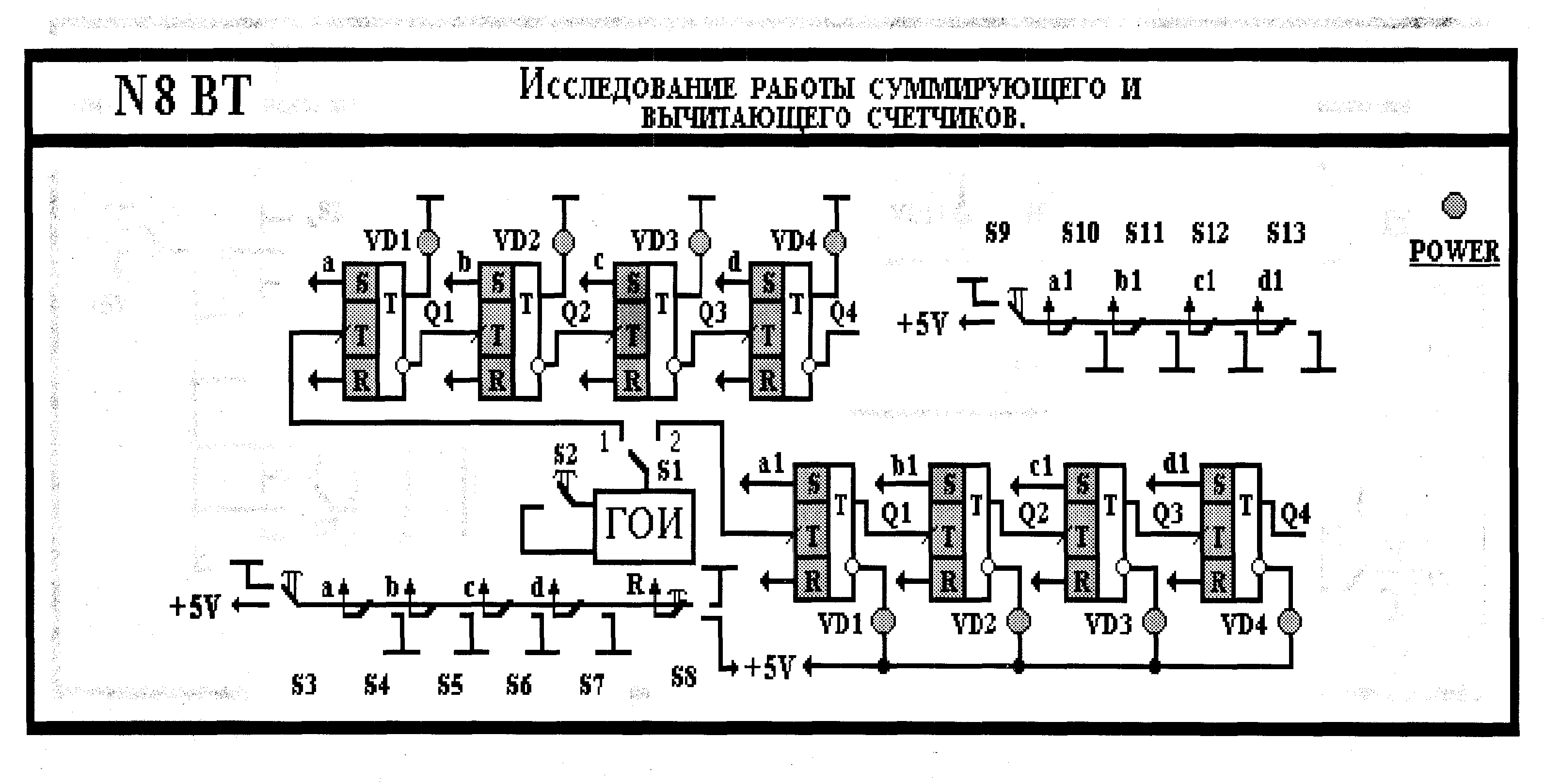
Внешний вид установки:
Исследуемые схемы монтируются на печатных платах из фольгированного стеклотекстолита, которые укрепляются на алюминиевой (дюралюминиевой) основе размером 430 на 200 мм, закрытой сверху прозрачным пластиком.
Цветное изображение исследуемых схем, название работы, переключатели находится между металлической основой и защитным пластиком. Питание стендов осуществляется от имеющихся источников, встроенных в лабораторные столы.
Приложение 2.
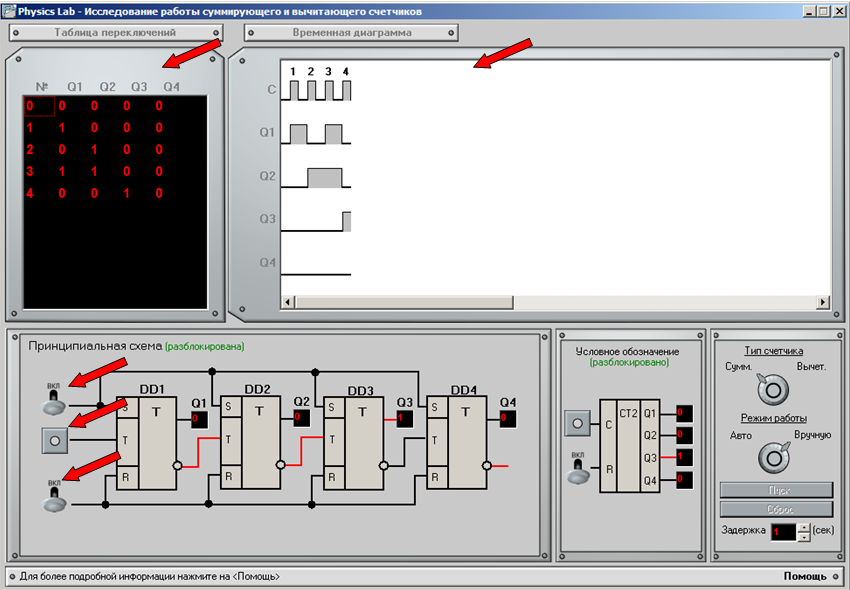
Шаг 1
На первом шаге необходимо выбрать направление тип счетчика (суммирующий или вычитающий).
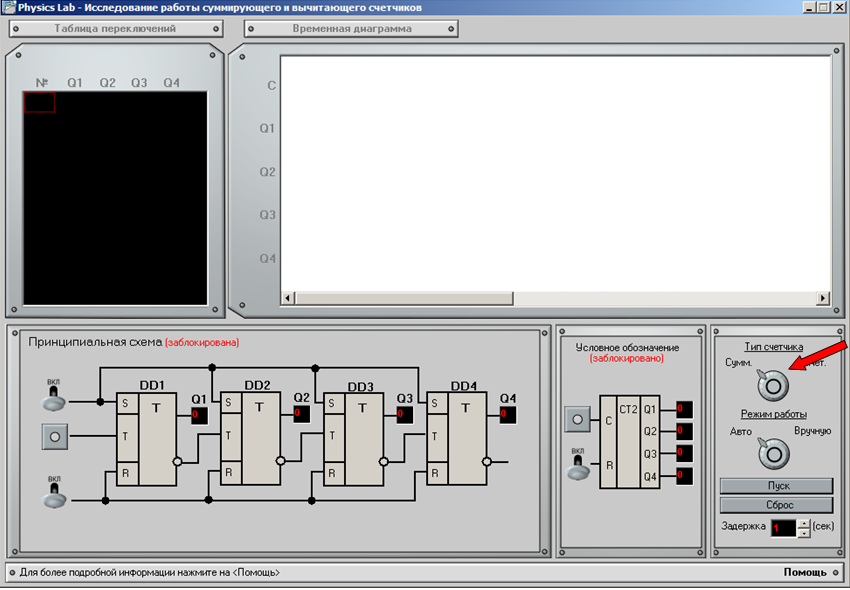
Шаг 2
Необходимо выбрать режим работы: автоматический или ручной. При автоматическом режиме работы вся система прогоняется по заранее установленным параметрам. При ручном режиме пользователь сам выбирает необходимые параметры и имеет больший контроль над системой.
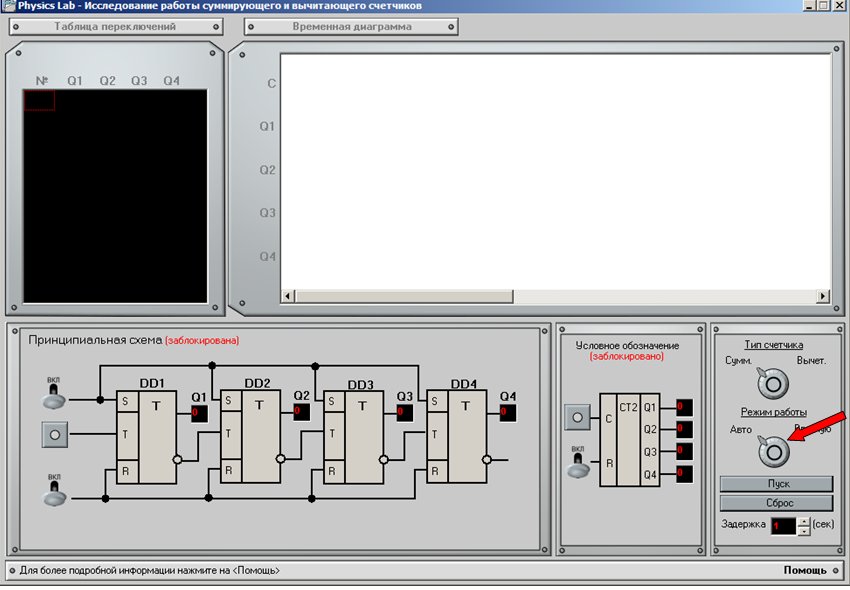
Шаг 3 (Автоматический режим)
Выбран автоматический режим. В этом режиме просто необходимо нажать на «Пуск» и указать время задержки импульсов, на рисунке эти элементы управления указаны стрелками. Нажатие на кнопку «Сброс» приводит систему в начальное состояние, она доступна только в автоматическом режиме. Более подробно об элементах см. Шаг 4.
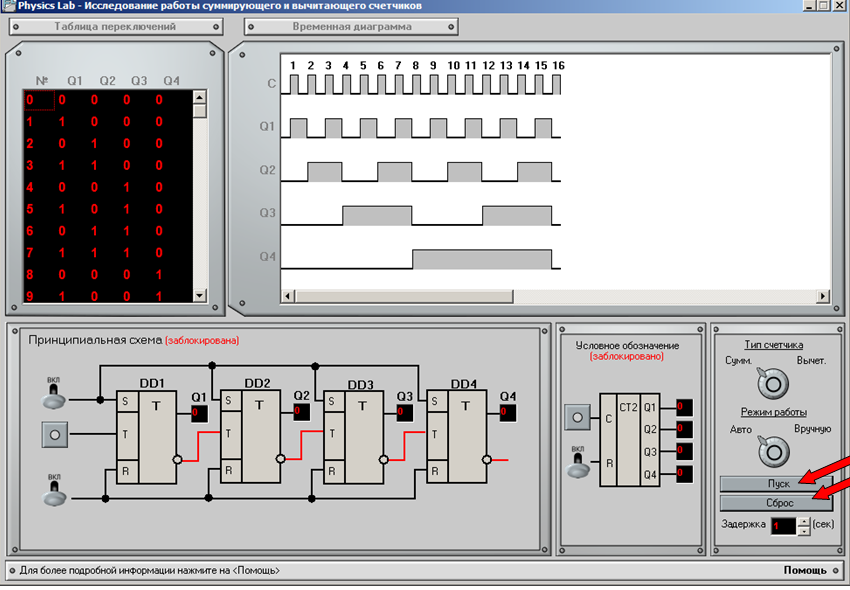
Шаг 4 (Ручной режим)
Для перехода в данный режим необходимо передвинуть переключатель на «Вручную». При этом будут доступны элементы управления на принципиальной схеме и условном обозначении (будет показано, что они разблокированы). Далее необходимо подавать импульсы на вход «С». При этом в системе будут происходить изменения, которые можно наблюдать в таблице переключений и временной диаграмме. Подавая напряжение на входы «S» или «R» (когда выбран вычитающий или суммирующий счетчик соответственно) можно привести систему в исходное состояние. Для дальнейшей работы их необходимо выключить.
Исследование работы интегральных схем сумматоров.
Цель лабораторной работы:
Подавая на входа различных интегральных схем сумматора цифровой код, построить таблицы истинности для них, убедиться в правильности счета.
Теоретическое введение.
Самый простейший сумматор - это сумматор по модулю два или узел неравнозначности (условное обозначение показано на рис 1). Он представляет собой устройство с двумя входами А и В, на выход (F) которого сигнал 1 появляется только в том случае, когда на входах действуют различные (неравнозначные) сигналы 0 и 1. Таблица 1 описывает его работу.
Таблица 1
А |
В |
F |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
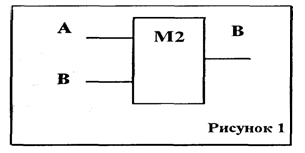
Название сумматора по модулю два (это устройство получило потому, что в случаях, когда сигналы А и В представляют собой однозначные двоичные числа, сигнал F на его
выходе соответствует сумме этих чисел по модулю т определяется не действительная суммы, а остаток, который получается от деления суммы на т.)
Имея таблицу составим структурную формулу.
F = ĀB+AB (1)
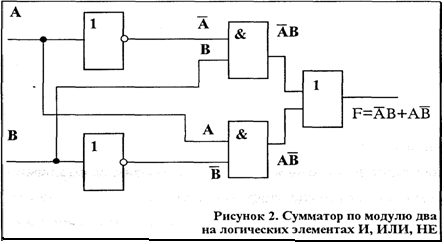
В зависимости от выбранной системы логических элементов сумматор по модулю два, выполняющий логическую операцию, в соответствии с формулой (1), может быть построен по разному.
На рис 2 приведена функциональная схема сумматора, построенная с помощью логических элементов И, ИЛИ, НЕ.
Полусумматор.
Полусумматором называется устройство, обеспечивающие выполнение операции сложения двух одноразрядных чисел А и В. В результате сложения в общем случае наряду с суммой может получиться перенос. Поэтому полусумматор имеет два выхода. С одного выхода снимается сигнал суммы S', а с другого - сигнал переноса Р’ условное обозначение полусумматора показано на рис 3.
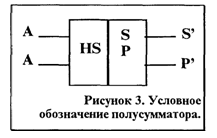
Таблица 2
А |
В |
S' |
Р' |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
Работа полусумматора описывается таблицей 2, сравнивая ее с таблицей 1, мы видим, что функция для суммы S (совпадает с функцией F сумматора по модулю два. Поэтому для построения схемы полусумматора можно воспользоваться уже рассмотренной схемой рис 2 и дополнить её устройствами, формирующими сигнал переноса Р'. Однако в целях экономии числа логических элементов в полусумматоре сумматор по модулю два целесообразно построить иначе. Для этого составим структурную формулу для суммы S ("по нулям", а для переноса Р'-" по единицам ".
(2)
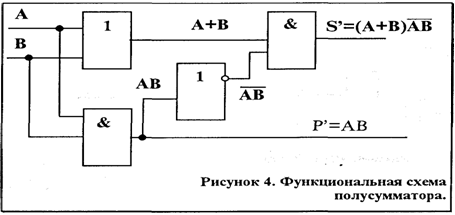
Мы видим, что функция Р (для переноса, будет входить в структурную формулу для суммы S (следовательно, для образования переноса не потребуется отдельной схемы.
Полный сумматор. - это устройство, предназначенное для сложения трех одноразрядных двоичных чисел А, В и С. Такая задача возникает при поразрядном сложении двух многоразрядных чисел, когда в качестве третьего слагаемого приходится учитывать перенос из предыдущего младшего разрыва. Правила выполнения операции сложения двоичных чисел иллюстрируются следующим примером:
Переносы |
1 1 |
Первое слагаемое А |
+0010001 |
Второе слагаемое В |
001101 |
Сумма S=A+B |
010110 |
Из этого примера видно, что в результате выполнения операции сложения в каждом разряде помимо суммы может образовываться перенос в очередной старший разряд. Поэтому полный сумматор так же, как полусумматор, должен иметь два выхода, на одном из которых вырабатывается сигнал суммы S, а на другом - сигнал переноса к Р. Построение функциональной схемы полного сумматора можно выполнить в том же порядке, как это делалось для полусумматора. Однако поступают проще: строят полный сумматор из двух полусумматоров (см рис5). Операция сложения 3-х одноразрядных чисел в той схеме расчленяется на две операции сложения двух одноразрядных чисел.
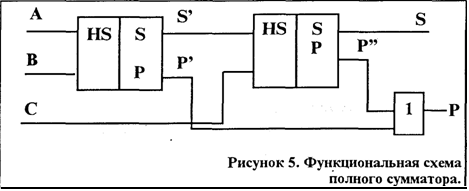
Сумматор.
Логика работы одноразрядного сумматора на три входа иллюстрируется таблицей 3, которая составлена по обычным правилам сложения трех двоичных цифр: слагаемых х, у и переноса из предыдущего разряда Рi
Таблица 3
X |
У |
Pi |
S |
Рi+1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
Выходы суммы и переноса в следующий (старший) разряд обозначены S и Рм соответственно. Для функций S и Рi+1 можно записать:
(3)
Преобразуя полученные выражения с помощью соотношений алгебры логики и используя различные логические элементы, можно получить различные схемы одноразрядных сумматоров.
Функциональное обозначение их приведены на рис 6.
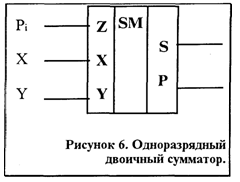
В зависимости от способа ввода слагаемых сумматоры делятся на два типа: последовательного и параллельного действия. В сумматоры первого типа коды чисел вводятся в последовательной форме, то есть разряд за разрядом (младшим разрядом вперед), в сумматоры второго типа каждое из слагаемых подается в параллельной форме, то есть всеми разрядами.
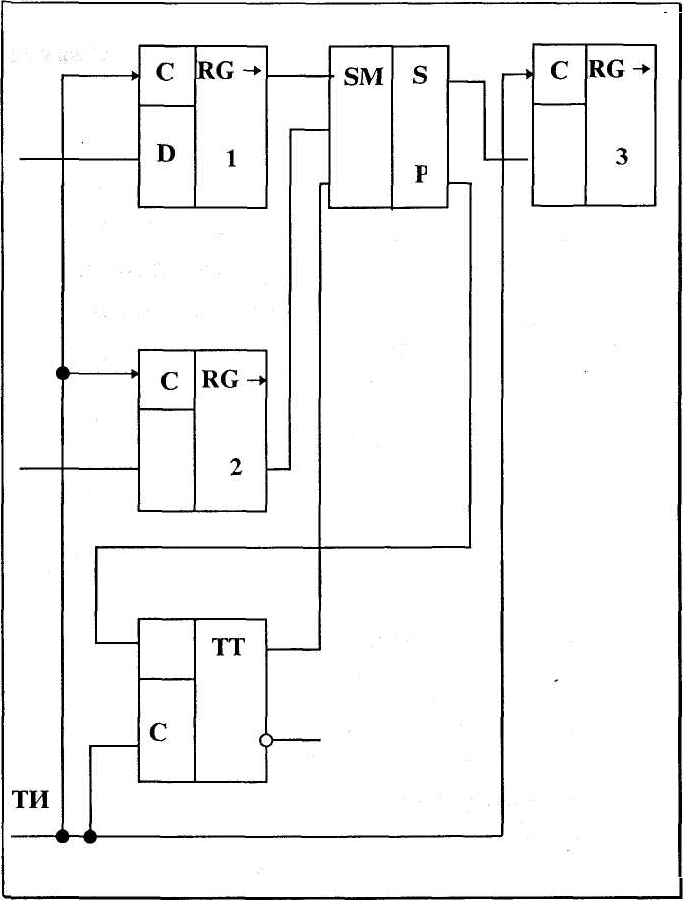
Сумматор последовательного действия (рис 7). Он состоит из одноразрядного сумматора, выход Pi+1, которого соединен с входом Pi через D- триггер. Изображённые на рисунке регистры сдвига не входят непосредственно в схему сумматора, они служат для подачи на входы сумматора разрядов слагаемых (регистры RG-1u RG-2) и приёма выдаваемых сумматором разрядов суммы (регистр RG-3).
Операция суммирования во всех разрядах слагаемых осуществляется с помощью одного и того же одноразрядного сумматора. Возможность такого построения сумматора достигается за счет того, что слагаемые поступают в последовательной форме. С первым тактовым импульсом на входы сумматора поступают из регистров RG-1 и RG-2 цифры первого разряда слагаемых а1 и Ь2 из D-триггера на вход Pi подается логический 0. Суммируя поданные на входы цифры, одноразрядный сумматор формирует первый разряд суммы S1 выдаваемый на вход регистра RG-3, и перенос Pi, принимаемый в D-триггер. Второй тактовый импульс осуществляет в регистрах сдвиг на разряд вправо; на входы одноразрядного сумматора при этом подаются цифры второго разряда слагаемых а2, Ь2 и перенос Р2; получающаяся цифра второго разряда суммы вдвигается в регистр RG-3, перенос Р3 принимается в триггере так далее.
Очевидное достоинство сумматора последовательного действия заключается в малом объёме оборудования, требуемого для его построения. Однако связанная с этим необходимость в последовательной обработке разрядов приводит к низкому быстродействию.
Сумматор параллельного действия.
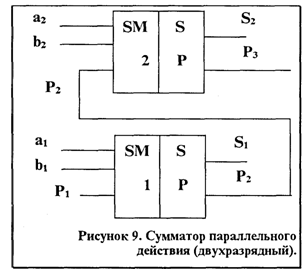
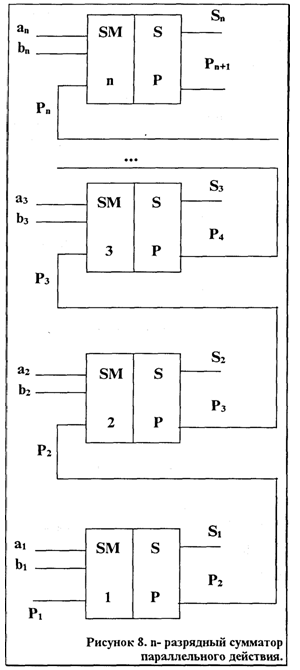
Если соединить два одноразрядных сумматора так как показано на рис 8, то мы получим. двухразрядный сумматор параллельного действия. Этот сумматор складывает двухразрядные числа. Цифры первого разряда слагаемых (a1 и b1) поступают на первый одноразрядный сумматор, цифры второго разряда слагаемых (а2 и в2) поступают на второй одноразрядный сумматор. Первый одноразрядный сумматор формирует на своих выходах цифру соответствующего разряда суммы S1 и перенос P2 передаваемый на второй одноразрядный сумматор. Во втором сумматоре происходит сложение трех слагаемых ал Ь2 и Р2 и формируются два сигнала на выходах суммы S2 и переноса Р3. Для сложения n-разрядных чисел соединяют вместе п одноразрядных сумматоров. Схема их соединения (рис 9) такая же как на рис 8.
При подаче слагаемых цифры их поступают параллельно (одновременно) на соответствующие одноразрядные сумматоры. Каждый из одноразрядных сумматоров формирует на своих выходах цифру соответствующего разряда суммы и перенос, передаваемый на вход одноразрядного сумматора следующего (более старшего) разряда.
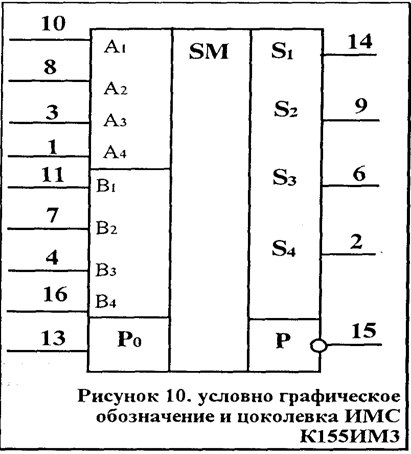
В сериях интегральных микросхем есть одно, двух и четырехразрядные сумматоры, которые можно объединить для получения сумматоров с любой разрядностью. В серию К 155, например, входят три сумматора: К 155 ИМ1- одноразрядный, К 155 ИМ 2 -двухразрядный, К 155 ИМ 3 - четырёхразрядный. Микросхема К 155 ИМ 3 см рис 10 представляет собой сумматор с параллельным поразрядным сложением и последовательным формированием сигнала переноса Рi+1. Рассмотрим пример сложения двух четырёхразрядных чисел таким сумматором, (см таблицу 4). Таблица 4
Операнд |
Разряд, i |
||||
|
4 |
3 |
2 |
1 |
0 |
Ai |
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
Bi |
|
1 |
0 |
0 |
1 |
|
|
|
|
|
|
Pi |
|
0 |
1 |
1 |
0 |
|
|
|
|
|
|
Pi+1 |
|
1 |
0 |
1 |
1 |
|
|
|
|
|
|
Si |
|
0 |
1 |
0 |
0 |
Результат |
1 |
0 |
1 |
0 |
0 |
Из приведенного примера видно, что процесс сложения идет последовательно (по разрядам), начиная с младшего, и для получения правильного результата в i-разряде мы должны сначала сложить числа в (И) - разряде и получить от него значение переноса Р/. Поэтому быстродействие сумматора с последовательным формированием сигнала переноса определяется случаем, когда при сложении А и В единица переноса возникает последовательно в каждом разряде, и, следовательно, время суммирования будет наибольшим и равным Тзд.р=п*tзд.р, где tзд.р — время задержки распространения сигнала переноса в одном разряде. Для повышения быстродействия создают схемы сумматоров с параллельным переносом, принцип построения подобен построению счетчиков со сквозным переносом (синхронные счетчики) таким сумматором со схемой ускоренного переноса является микросхема К561ИМ1.
Методика исследования.
Работа интегральных схем сумматоров.
«А» виртуальная реализация лабораторной работы
Прежде чем приступить к выполнению виртуальной лабораторной работы необходимо инсталлировать программное обеспечение CircuiMaker2000. Программа находится на настоящем диске в папке CM2000. Для инсталляции запустите файл SetupCM2000.exe, выберите стандартный тип установки и следуйте указаниям инсталлятора. Пароль для инсталляции находится в файле Password.txt в той же папке. После установки установите пакет обновлений файл CM2000SP1.exe. Инструкция по работе с программой CircuiMaker2000 находится в Приложении №2. В ряде случаев имеются отличия виртуальной лабораторной работы от ее стендовой реализации. Критерием правильности является верное выполнение таблицы истинности.