Занятие 6
Случайная величина Х распределена по закону, определяемому плотностью распределения вероятностей вида:
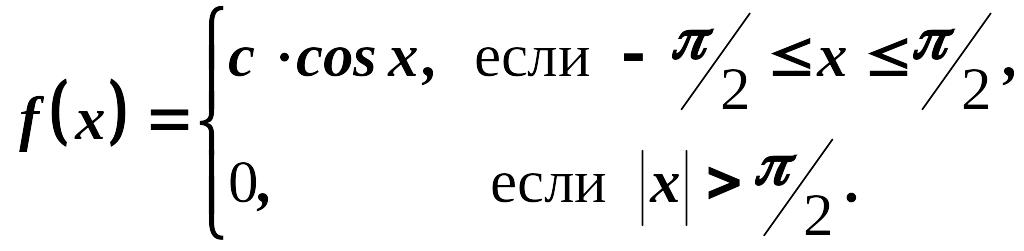
Найти
константу с,
вычислить
,
М(х) и
D(х).
Ответ:
с=0,5,
=
,
М(х)=0,
D(x)=
.
2. В лотереи один выигрыш по 1000 р., два по 500 р. и 5 по 100 р. Определить общее количество билетов, если математическое ожидание суммы выигрыша равно 5 р.
Ответ:
.
3.
Охотник, имеющий три патрона, стреляет
по зайцу, пока не попадет или не кончатся
патроны. Составить закон распределения
числа использованных патронов, если
вероятность попадания при одном выстреле
равна
.
Найти математическое ожидание и
дисперсию.
Ответ:
.
4.
Пассажир может ждать лётной погоды трое
суток, после чего едет поездом. По
прогнозам метеорологов вероятность
летной погоды в первые сутки равна 0,5;
во вторые – 0,6; в третьи – 0,8. Пусть
- число полных суток до отъезда пассажира.
Составить ряд распределения случайной
величины
,
найти математическое ожидание и
дисперсию.
Ответ:
.
5. Студент выучил 30 вопросов из 40. Экзаменационный билет содержит 3 вопроса. Составить закон распределения числа правильных ответов на вопросы билета, найти его математическое ожидание и дисперсию.
Ответ:
.
6. Игральная кость брошена три раза. Составить закон распределения числа выпадений 5 и найти все числовые характеристики.
Ответ:
.
7.
Найти
,
для плотности распределения заданной
графически
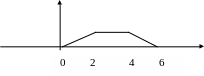
Ответ:
.
Самостоятельная работа
1. Функция распределения случайной величины задана интегральной функцией:
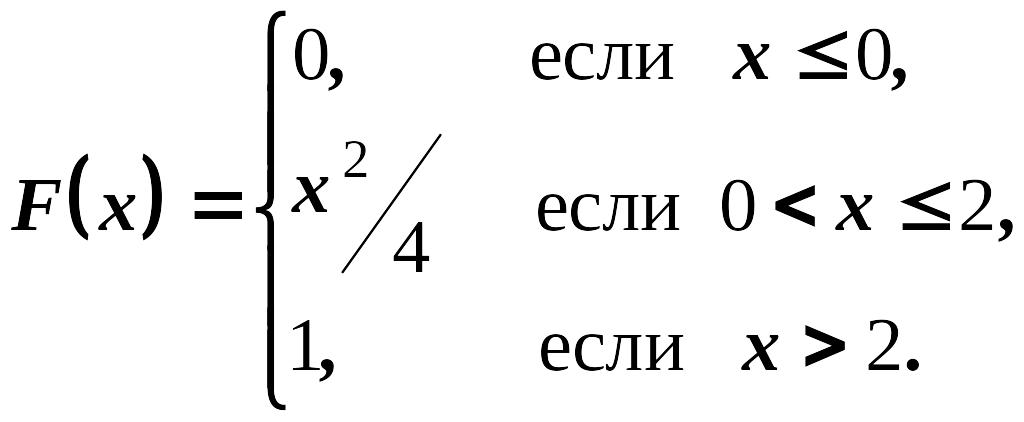
Вычислить
,
М(х), D(х),
А, Е.
Ответ:
=0,75,
М(х)=
,
D(x)=
,
А=
,
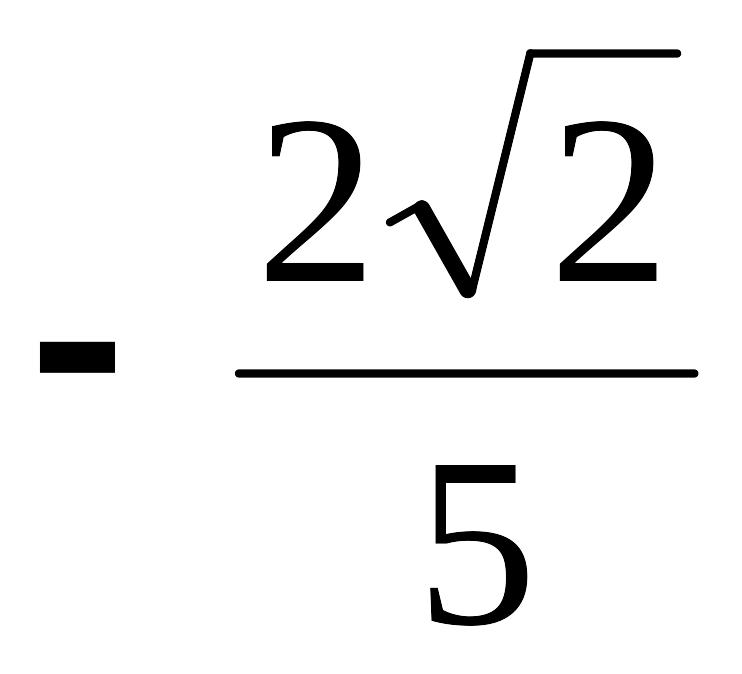Е=
.
2. Случайная величина задана функцией распределения
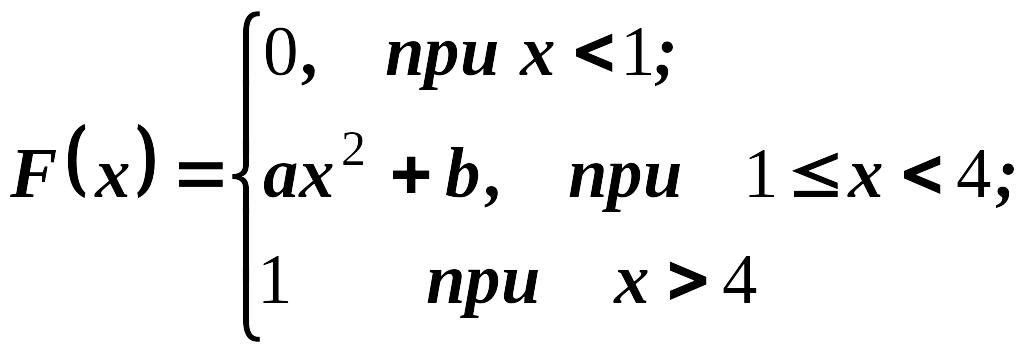
Найти:
и
,
математическое ожидание, дисперсию.
Ответ:
.
3. Студент сдает экзамены с вероятностями 0,8; 0,7; 0,6. Найти математическое ожидание и дисперсию числа сданных экзаменов.
Ответ:
.
4. В партии из 5 изделий 2 имеют скрытый дефект. Реализовано 4 изделия. Составить закон распределения числа качественных изделий среди реализованных. Найти математическое ожидание и дисперсию для данного распределения.
Ответ:
.
Занятие 7
1. Случайная величина Х распределена по закону Коши, определяемому функцией распределения вероятностей:
Выбрать коэффициенты а, b и c таким образом, чтобы данное распределение соответствовало случайной величине непрерывного типа.
Ответ:
b=
,
c=
.
2. Из урны содержащей 4 белых и 6 чёрных шаров, случайным образом и без возвращения извлекается 3 шара. Случайная величина Х - число белых шаров в выборке. Составить закон распределения и найти М(х), D(x), А, Е.
Ответ:
М(х)=
,
D(x)=
,
А=
,
Е=
.
3.
Для нормального закона распределения
известно математическое ожидание
и
.
Найти вероятность
.
Ответ: 0,7745.
4. В нормально распределенной совокупности 15% значений меньше 12 и 40% значений больше 16,2. Найти среднее значение и среднее квадратическое отклонение данного распределения.
Ответ:
5. Найти дисперсию дискретной случайной величины Х - числа появлений события А в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что М(Х)=0,9.
Ответ:
6.
Для биноминального закона распределения
известно, что
и
.
Найти возможные значения коэффициента
ассиметрии.
Ответ:
.
Самостоятельная работа
1. Случайная величина Х распределена по закону равнобедренного треугольника в интервале (-а, а) (закон Симпсона), если она непрерывного типа и её плотность распределения вероятностей имеет вид, изображённый на рисунке:
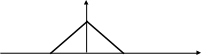
y=f(x)
-а 0 а х
Написать выражение для f(x) и F(x). Вычислить D(x).
Ответ:
D(x)=
,
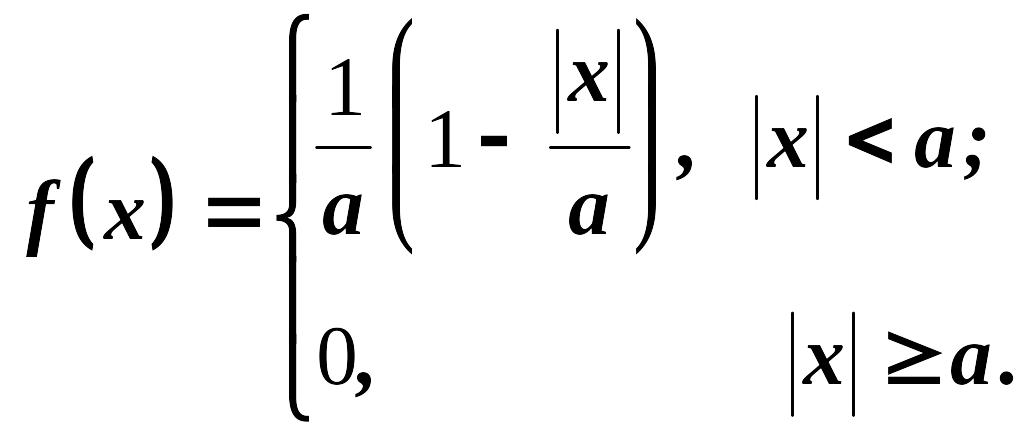
2.
Деталь, изготовленная автоматом,
считается годной, если отклонение Х
контролируемого размера от номинала
не превышает 10 мм. Точность изготовления
деталей характеризуется выборочным
средним отклонением
.
Считая, что для данной технологии
и Х
нормально распределена, выяснить,
сколько процентов годных деталей
изготовляет автомат.
Ответ:
.
3. Коробки с шоколадом упаковываются автоматически. Их средняя масса 1,06 кг. Известно, что 5% коробок имеют массу меньшую 1 кг. Каков процент коробок, масса которых превышает 940 г?
Ответ:
4. Сколько раз нужно бросить игральную кость, для того, чтобы дисперсия выпадения 6 очков была равна 10.
Ответ:
.