4.3. Показатели относительного рассеивания

Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер рассеивания в различных распределениях.

Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины.
Коэффициент вариации используется для оценки типичности средних величин. Совокупность считается количественно однородной, если v<33%.
Эмпирическое корреляционное отношение показывает тесноту связи группировочного признака и результативного. группировочный признак целиком определяет вариацию результативного; влияние группировочного признака на результативный равно 0. Соотношения Чеддока дают качественную оценку тесноты связи.

Задача 1. Имеются данные о возрастном составе рабочих цеха (лет): 18, 38, 28, 29, 26, 38, 34, 22, 28, 30, 22, 23, 35, 33, 27, 24, 30, 32, 28, 25, 29, 26, 31, 24, 29, 27, 32, 25, 29, 29. Построить интервальный ряд распределения для 7 групп и графическое изображение ряда. Вычислить показатель центра распределения, т.е среднее значение возраста ( ) и показатели вариации.

Решение. 1) Определим величину интервала группировки

Построим интервальный ряд распределения рабочих по возрасту.

Группы рабочих по возрасту, (х)	Число рабочих, F
18-21 21-24 24-27	1 3 6	1 4 10	19,5 22,5 25,5	19,5 67,5 153,0	84,64 38,44 10,24	84,64 115,32 61,44
27-30 30-33 33-36 36-39	10 5 3 2	20 25 28 30	28,5 31,5 34,5 37,5	285,0 157,5 103,5 75,5	0,04 7,84 33,64 77,44	0,4 39,2 100,92 154,88
Итого	30	–	–	861,0	–	556,8

2) Расчет показателя среднего возраста рабочих года

3) Расчет структурных средних:

а) Модальный интервал 27-30 лет, так как f_max = 10. Значение моды

б) Место медианы .

Медианный интервал приходится на группу 27-30 лет находящуюся в середине нечетного ряда

.

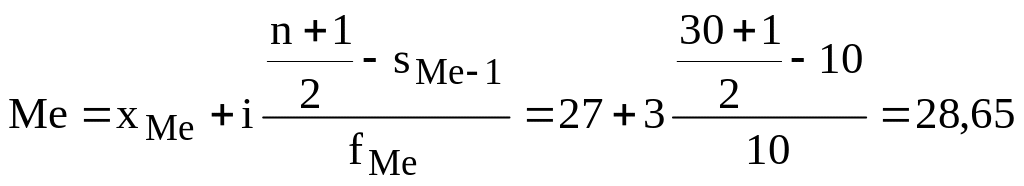3) Показатели вариации

Среднее абсолютное линейное отклонение года.

Среднее квадратическое отклонение 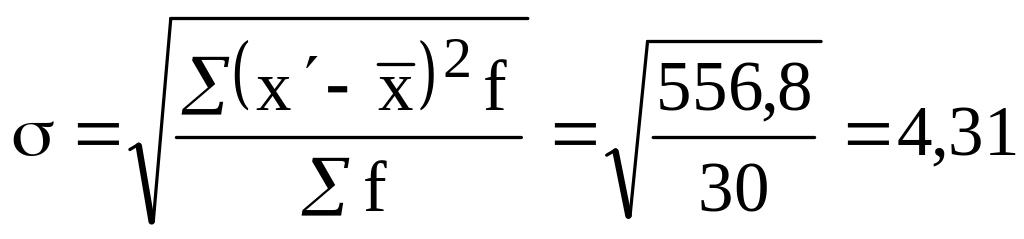года.

Коэффициент вариации .

Вариация незначительна, следовательно, совокупность однородна.