Лабораторная работа №28 Изучение вероятностных алгоритмов диагностики

Студент должен знать: что такое случайное событие, классическое и статическое определения вероятности случайного события; зависимость событий; условная вероятность события; вероятность произведения независимых и зависимых событий, формула Байеса; задачи медицинской кибернетики и математики в области клинической диагностики; диагностические алгоритмы и их виды; информационный или диагностический вес симптома (только для УИРС).

Студент должен уметь: по статистическим медицинским данным составлять диагностическую таблицу для вероятностного диагностического алгоритма; вычислять по данным этой таблицы условную вероятность заболевания при наличии нескольких симптомов, информационный вес симптома (только для УИРС).

Краткая теория

I. Введение

В настоящее время математиками и врачами совместно разработаны несколько методов вычислительной диагностики: детерминистские логические, метод фазового интервала, метод линейных дискриминантных функций, информационно-вероятностный и др. В данной лабораторной работе рассматривается только последний - вероятностный, основанный на формуле Байеса (см. ниже).

Применение вероятностного метода диагностики требует предварительной статистической обработки уже имеющегося клинического материала в виде большого количества историй болезни.

Будем считать, что у больного одновременно может быть только одна болезнь из какой-то группы из n заболеваний (диагнозов), обозначаемых d₁, d₂,... ,d_n. Таким образом, задачей диагностики является выбор одной, наиболее вероятной болезни из группы, т.е. речь идёт о дифференциальной диагностике.

Для распознавания болезней используют признаки, характеризующие какие-либо свойства исследуемого больного (обозначаемые S₁, S₂,... ,S_m). Например, возраст, давление крови, СОЭ и т.п.

Каждый признак может принимать ограниченное число значений, причем под значением понимают также определенный диапазон изменения признаков. Отдельное значение (или диапазон значений) признака обозначается верхним индексом К ( , , ,… ) и называется симптомом. Например, признак - частота пульса, его значения (симптомы K = 1,2,3): - частота 80 ударов минуту и менее, - от 81 до 100 ударов и - более 100 ударов в мин. Минимальное число значений признака - ДВА: - признак есть; - признака нет. Например: наличие и отсутствие боли, кашля; возраст меньше 50 и больше 50 лет и т.д.

Для применения вероятностного алгоритма диагностики надо предварительно по статистическим данным найти вероятности симптомов и болезней (см. ниже), за которые приближенно принимают их относительные частоты.

Относительной частотой случайного события А называют отношение числа n_A случаев появления этого события А к общему числу N произведенных испытаний (опытов, наблюдений), при которых оно могло появиться - n_A/N. При большом числе анализируемых историй болезни вероятность события Р(А) и соответствующая ей частота n_A/N не слишком отличаются друг от друга:

P(A)= n_A/N

(далее вместо знака " ", для простоты, будем писать знак равенства "=", но помнить о приближении).

Вероятность симптома равна отношению числа больных имеющих этот симптом, к общему числу N больных во всей группе заболеваний:

P( )= (I)

Вероятность болезни d_j равна отношению числа больных n_j с этим заболеваем к общему числу N больных во всей группе заболеваний:

P(d_j)= (2)

Условная вероятность Р( /dj) симптома при наличии заболевания d_j равна ношению числа njik больных болезнью d_j и имеющих при этом симптом . к общему числу больных n_j, страдающих этой болезнью:

P( /dj)= (3)

Условную вероятность Р( /dj) болезни d_j при наличии одного симптома можно было бы подсчитать по формуле:

P(dj / )= , (4)

где (повторим еще раз)

n_jik - число больных болезнью d_j и имеющих симптом , а n_ik - общее число больных в группе из n заболеваний, имеющих симптом .

Если бы мы знали последние вероятности, P(d_j / ), то могли бы установить наиболее вероятный диагноз при наличии у больного симптома (по наибольшей из P(d_j / )).

Однако, во-первых, у больного, наверняка, обнаружены одновременно несколько симптомов. Во-вторых, в современной медицинской литературе практически отсутствуют сведения о частоте встречаемости различных болезней при наличии соответствующих симптомов, т.е. о приближенном значении P(d_j / ). В ней можно найти лишь данные об относительной частоте тех или иных симптомов при соответствующих заболеваниях (т.е. P( /d_j)) хотя и таких сведений относительно мало. Вследствие этих и еще ряда причин, вероятность P(d_j / ) заболевания d_j при данном симптоме рассчитывают не по формуле (4), а по формуле Байеса (5):

P(d_j / )= (5)

где P( ) может быть найдена через P(d_j) P( /d_j) по формуле полной вероятности (6):

P( )= P(d_j)^.P( /d_j) (6)

Подставляя выражения для P( ) из (6) в (5), получаем расчетную формулу для диагностики:

P(dj / )=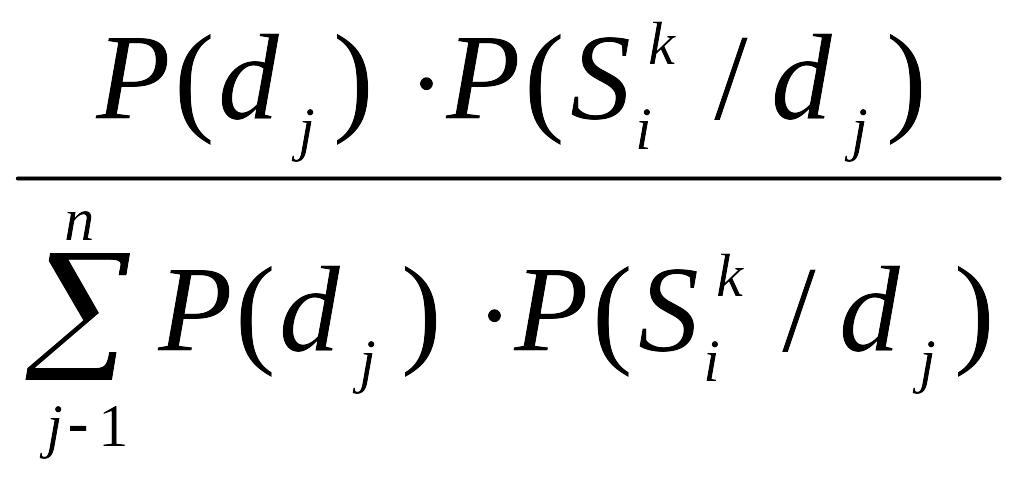 (7)

Вычисленные в результате статистической обработки историй болезней значения условных вероятностей симптомов P( /d_j) и вероятностей заболеваний P(d_j) располагают в виде диагностической таблицы (рис.1).

В таблице по вертикали откладываются заболевания ,, соответствующие рассматриваемому классу из n заболеваний, а по горизонтали - различные симптомы . На пересечении строки и столбца записывается вычисленная условная вероятность Р( / ) появления симптома при заболевании . В крайний левый столбец заносятся вероятности Р( ) заболевания в данной местности, в данное время и для определенной группы населения, к которой относится диагностируемый больной.

Оформленная таким образом диагностическая таблица уже сама по себе имеет громадную ценность (ведь ее составляют высококвалифицированные врачи-специалисты по этой группе заболеваний). По ее данным вычисляют по формуле (7) условные вероятности Р( / ) каждой из имеющихся в таблице болезни при условии что у больного имеется симптом . Последовательно вычислив все вероятности, затем можно выбрать один из n. возможных диагнозов - тот, вероятность Р( / ) которого наибольшая. Обычно указывают еще 2-3 диагноза, следующих за ним по величине (вероятности)- как информация врачу о других возможных диагнозах.

Однако различия между вероятностями заболеваний при использовании для их подсчета только одного симптома обычно слишком малы, чтобы можно с большей уверенностью выбрать одно из заболеваний и поставить правильный диагноз.

Поэтому используют для расчетов вероятности всех симптомов, установленных у больного. Если считать симптомы независимыми друг от друга, то формула Байеса принимает вид (например, для случая четырех симптомов , , , ):

Р( / , , , ) 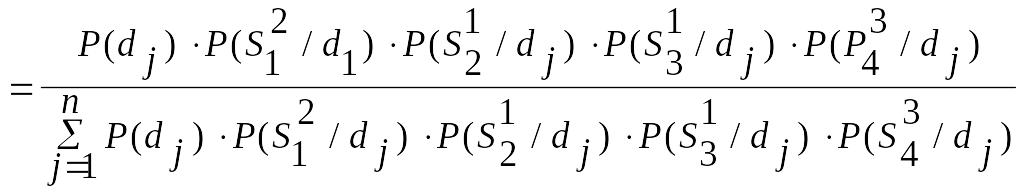(8)

В случае зависимых симптомов используют другие модификации формулы Байеса (здесь не будем рассматривать), требующие специального изучения и подсчета вероятностей различных сочетаний симптомов (симптомокомплексов).

На данном этапе развития любой вычислительный диагностический метод является только одним, хотя и, очень эффективным, из диагностических средств в помощь врачу (как, например, фонендоскоп, ЭКГ, рентген). Окончательный диагноз с учетом полученных при вычислениях количественных показателей и вероятностей может быть сделан только самим врачом на основании его опыта.