
Лабораторная работа №2 Соответствия и отношения
В качестве исходных данных студент должен использовать множества U, A, B, C, D, сформированные в лабораторной работе №1. Для данных множеств необходимо выполнить следующее:
1. Найти какое-либо соответствие R между элементами множества A и элементами множества B (то есть найти <A, B, R>). Представить данное соответствие в словесном, графическом и табличном виде, а также в виде множества пар. Определить, является ли оно полным слева, сюръективным, функциональным, инъективным или биективным (пояснить, почему).
2. Выполнить задание 1 для множеств A и C. Закон соответствия должен быть отличным от закона в п. 1.
3. Выполнить задание 1 для множеств B и D. Закон соответствия должен быть отличным от закона в п. 1 и 2.
4. Выполнить задание 1 для множеств C и B. Закон соответствия должен быть отличным от закона в п. 1-3.
5. Найти, если такое возможно, отображения A→B, B→C, C→D. Каждое отображение задать словесно и графически.
6. Найти, если такое возможно, функции A→B, B→C, C→D. Каждую функцию задать словесно и графически.
7. На множестве A задать (если это возможно) следующие бинарные отношения, представив их в словесном и графическом виде:
а) отношение, обладающее свойством рефлексивности;
б) отношение, обладающее свойством антирефлексивности;
в) отношение, обладающее свойством симметричности;
г) отношение, обладающее свойством антисимметричности;
д) отношение, обладающее свойством транзитивности;
е) транзитивное замыкание;
ж) отношение эквивалентности;
з) отношение частичного порядка (строгого или нестрогого);
и) отношение доминирования;
к) отношение толерантности.
Законы отношений в пунктах а-к могут повторяться (если это уместно). В случае, если какое-либо из отношений на данном множестве задать невозможно или весьма затруднительно, студент должен пояснить, почему. Графически отношение проще всего представить в виде элементов множества, расставленных по кругу и соединенных стрелками в соответствии с законом отношения.
8. Выполнить задание 7 для множества B. Законы отношений могут повторяться с законами из задания 7.
9. Выполнить задание 7 для множества C. Законы отношений могут повторяться с законами из заданий 7 и 8.
10. Выполнить задание 7 для множества D. Законы отношений могут повторяться с законами из заданий 7-9.
11. Выполнить задание 7 для множества U. Законы отношений могут повторяться с законами из заданий 7-10.
Пример выполнения работы
Рассмотрим пример для множеств A и B из примера для предыдущей лабораторной работы:
A |
B |
4 – плоскогубцы 10 – нож 12 – кисточка 13 – шпатель 17 – уровень 20 – ведро 22 – клещи 26 – валик 29 – стамеска 30 – рулетка |
1 – молоток 3 – отвертка 4 – плоскогубцы 10 – нож 11 – гаечный ключ 20 – ведро 22 – клещи 24 – паяльник 25 – домкрат 28 – фонарик |
Для того, чтобы задать соответствие <A, B, R>, необходимо определить его закон. Представим ситуацию, когда мастер пришел на ремонт некоего объекта, но забыл захватить свой ящик с инструментом. Он попросил инструмент у присутствующих на объекте людей, и они дали ему свой ящик, содержимое которого, разумеется, отличается от содержимого ящика мастера. Мастеру придется выкручиваться, используя вместо привычных ему инструментов (элементы множества B) те, что есть в данном ему наборе (элементы множества A). При этом вполне нормально, что некоторые инструменты будут использованы не по своему прямому назначению. Например, в наборе A не оказалось молотка, но забить гвоздь, при желании, можно большими плоскогубцами. Таким образом, плоскогубцы будут играть роль молотка, то есть соответствовать молотку. В словесном виде такой закон можно сформулировать следующим образом: R = «элемент aiA при необходимости может заменить (быть использован вместо) элемент biB».
Применим фантазию и изобразим подобное соответствие в графическом виде:

Элементы множеств, участвующие в соответствии, выделены жирным шрифтом. Можно констатировать, что данное соответствие не является полным слева, сюръективным, функциональным, инъективным и биективным. Однако отсутствие данных признаков никак не уменьшает полезности соответствия для нашего мастера.
В табличном виде соответствие можно представить так:
|
1 |
3 |
4 |
10 |
11 |
20 |
22 |
24 |
25 |
28 |
4 |
1 |
|
1 |
|
1 |
|
1 |
|
|
|
10 |
|
1 |
|
1 |
|
|
1 |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
1 |
|
|
|
|
22 |
|
|
|
1 |
1 |
|
1 |
|
|
|
26 |
|
|
|
|
|
|
|
|
|
|
29 |
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
В виде множества пар наше соответствие выглядит следующим образом: <A, B, R> = {<плоскогубцы, молоток>, <плоскогубцы, плоскогубцы>, <плоскогубцы, гаечный ключ>, <плоскогубцы, клещи>, <нож, отвертка>, <нож, нож>, <нож, клещи>, <ведро, ведро>, <клещи, нож>, <клещи, гаечный ключ>, <клещи, клещи>}.
Учитывая выбранный нами закон соответствия, сочетание <ведро, ведро> является вполне нормальным, поскольку это разные ведра: первое ведро является элементом множества A (то ведро, которое дали мастеру), а второе – элементом множества B (то ведро, которое мастер забыл взять с собой).
Рассмотрим отдельно множество A и зададим на нем бинарное отношение aQb, обладающее свойством рефлексивности. Сформируем следующий закон отношения: Q = «рукоятка от элемента a может подойти элементу b». Понятно, что рукоятка от любого инструмента подходит для самого же себя (рефлексивность) и, возможно, подойдет и для ряда других инструментов. Графически данное отношение на множестве A показано на следующем рисунке. Если при защите лабораторной работы правильность составленного отношения вызывает у преподавателя сомнения, студент должен быть готов дать необходимые пояснения.
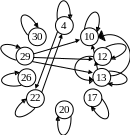
A |
4 – плоскогубцы 10 – нож 12 – кисточка 13 – шпатель 17 – уровень 20 – ведро 22 – клещи 26 – валик 29 – стамеска 30 – рулетка |
