Определение определителя системы
Вес пути определяется как произведение соответствующих весов контуров.
∆=1-(K1+K2+K3+K4)+(K1*K2+K1*K3+K1*K4+K2*K3+K2*K4+K3*K4)-(K1*K2*K3*K4)
∆=1-(-0,07028)+(0,406024)-(0,000378)=1,475926
1.3 Определение всех элементарных путей из узла х в узел у
Определим все пути, используя данные таблицы 1.
1
2
3
4
6
5
P1= r1*r3*r4*r6*r9=0,1944
Δi=1-(0,4+0,9+0,9)+(0,4*0,9)=-0,84
1.4 Определение передаточной функции системы от х к у по формуле Мезона
,
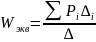где
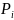-вес
i-го пути от
входа к выходу,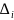
-минор
i-го пути,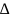
-определитель
графа.
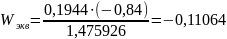
1.5 Выделение 2 – 3 несвязанных контуров как подсистем и определение их связности
7
1
2
S 1:
3
4
S 2:
5
6
S 3:
Определим вес каждого контура: K1=1,2*(-0,9)*0,5=-0,54; K2=0,8*0,9=0,72;
K3=0,5*0,2=0,1
Методом Вавилова и Майера определим силы связанности:
∆S1=1- K1=1-(-0,54)=1,54
∆S2=1- K2 =1-0,72=0,28
∆S3=1- K3 =1-0,1=0,9
Рассчитаем определитель несвязных подсистем:
∆∞=∆S1*∆S2*∆S3=0,38808, где ∆∞-определитель разомкнутой системы.
Определим
силу связности графа:
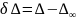
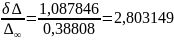
Данное значение
входит в интервал, соответствующий
сильной связности подсистем: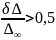
1.6 Расчет изменения
энтропии системы и вероятности нахождения
в каждом из узлов. Используя
граф системы (рисунок 1) и данные таблицы
1, рассчитаем изменение энтропии системы.
Энтропия
показывает степень хаотичности и
неопределенности в системе.
Понятие
энтропии введено Больцманом для
термодинамических систем: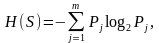
Начальная
энтропия:
Р=Р1=Р2=…=Р7=1/7;
Hнач.=
-7(1/7log21/7)=2,807.
Pi
– вероятность нахождения системы в i-м
состоянии
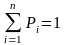
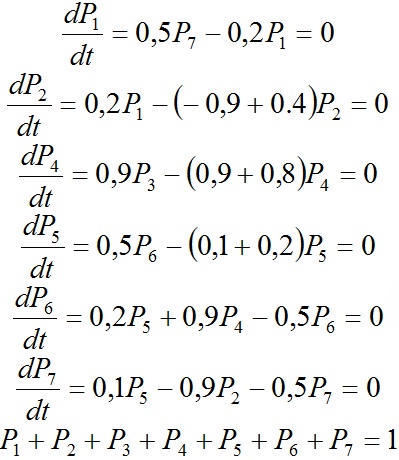Установившееся
значение вероятности нахождения системы
в i-м состоянии определяется из условия:
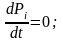Тогда
для системы с n состояниями имеем систему
из (n + 1) уравнений с n неизвестными:
;
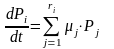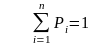
Одно из уравнений можно отбросить, так как оно может быть получено из (n - 1) оставшихся.
|
Р1 |
Р2 |
Р3 |
Р4 |
Р5 |
Р6 |
Р7 |
|
|
1 |
-0,2 |
0 |
0 |
0 |
0 |
0 |
0,5 |
0 |
|
2 |
0,2 |
0,5 |
0 |
0 |
0 |
0 |
0 |
0 |
|
3 |
0 |
0 |
0,9 |
-1,7 |
0 |
0 |
0 |
0 |
|
4 |
0 |
0 |
0 |
-0 |
-0,3 |
0,5 |
0 |
0 |
|
5 |
0 |
0 |
0 |
0,9 |
0,2 |
-0,5 |
0 |
0 |
|
6 |
0 |
-0,9 |
0 |
0 |
0,1 |
0 |
-0,5 |
0 |
|
7 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
P1= -0.2673
P2= 0.1069
P3= 0.2693
P4= 0.1426
P5= 0.4277
P6= 0.4277
P7= -0.1069
Найдем
энтропию Н и ΔН:
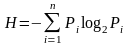
Делаем вычисления в программе «MATLAB R2009b» :
>> H=(0.2673*log2 (0.2673)+0.1069*log2 (0.1069)+0.2693*log2 (0.2693)+0.1426*log2 (0.1426)+0.4277*log2 (0.4277)+0.4277*log2 (0.4277)+0.1069*log2 (0.1069))
H =
-3.1570
>> HO-H
ans =
5.9644
ΔН= Н0-Н=5.9644>0, следовательно, Н уменьшилось, значит, система упорядочилась.