
- •Курсовой проект
- •«Теория систем»
- •1 Выделение подсистем на основе некоторой меры
- •2 Выбор типов шкал
- •3 Определение порядка проведения работ
- •4 Построение моделей систем
- •5 Анализ иерархий
- •1 Выделение подсистем на основе некоторой меры
- •Определение матриц смежности, инцидентности и контуров
- •Определение определителя системы
- •1.3 Определение всех элементарных путей из узла х в узел у
- •1.4 Определение передаточной функции системы от х к у по формуле Мезона
- •1.5 Выделение 2 – 3 несвязанных контуров как подсистем и определение их связности
- •2 Выбор типов шкал
- •3 Определение порядка проведения работ
- •4 Построение моделей системы
- •5 Анализ иерархий
5 Анализ иерархий
Методом анализа иерархий обосновать выбор действия, определенного вариантом (таблица 7).
Таблица 7 – Действия
Вар. |
Действие |
21 |
Покупка автомагнитолы |
1 Выделение подсистем на основе некоторой меры
Определение матриц смежности, инцидентности и контуров
По исходным данным строится граф системы (рисунок 1). Матрица смежности определяется как матрица размером n×n, где n – количество вершин графа.
Г

Вход
Выход
Ребро
Вершина
Вес
раф – геометрическая фигура, построенная на множестве вершин V = {v1, v2, … vm} и ребер R = {r1, r2, … rn}Рисунок 1 – Граф системы
Матрицы смежности и инцидентности определяются по графу системы и имеют вид (рисунок 2 и 3).
Рисунок 2 – Матрица смежности
|
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V7 |
V1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
V2 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
V3 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
V4 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
V5 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
V6 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
V7 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
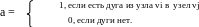
Число единиц в матрице А равно числу дуг n. Если возвести матрицу А в k-ю степень, то каждый элемент матрицы Аk будет равен числу путей из узла vi в узел vj длиной в k дуг. Очевидно, что если число узлов m, максимальная степень k, в которую нужно возвести А для определения самого длинного пути, равна (m – 1).
Рисунок 3 – Матрица инцидентности
|
r1 |
r2 |
r3 |
r4 |
r5 |
r6 |
r7 |
r8 |
r9 |
r10 |
V1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
V2 |
-1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
V3 |
0 |
0 |
-1 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
V4 |
0 |
0 |
0 |
-1 |
1 |
1 |
0 |
0 |
0 |
0 |
V5 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
-1 |
0 |
V6 |
0 |
0 |
0 |
0 |
0 |
-1 |
-1 |
0 |
1 |
0 |
V7 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
-1 |
0 |
1 |
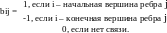
Для неориентированных:
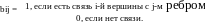
Матрица контуров определяется по количеству контуров графа (рисунок 4).
Рисунок 4 – Матрица контуров
|
r1 |
r2 |
r3 |
r4 |
r5 |
r6 |
r7 |
r8 |
r9 |
r10 |
K1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
K2 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
K3 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
K4 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
Rgxm{kij}, где g-количество контуров.
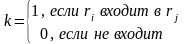 Рассчитаем
веса контуров:
Рассчитаем
веса контуров:
K1=1,2*0,4*0,9*0,9*0,5*0,1*0,5=0,00972
K2=1,2*0,9*0,5=0,54
K3=0,8*(-0,9)=-0,72
K4=0,5*0,2=0,1
