4. Перевод из восьмеричной и шестнадцатеричной систем в двоичную

Для восьмеричной — преобразуем по таблице в триплеты, д ля шестнадцатеричной — преобразуем по таблице в квартеты:

0 000 4 100 1 001 5 101 2 010 6 110 3 011 7 111

0 0000 4 0100 8 1000 C 1100 1 0001 5 0101 9 1001 D 1101 2 0010 6 0110 A 1010 E 1110 3 0011 7 0111 B 1011 F 1111

преобразуем 548 → 101 100 2C16 → 0010 1100

6. Перевод из двоичной системы в 8- и 16-ричную

   Перевод дробной части из двоичной системы счисления в системы счисления с основаниями 8 и 16 осуществляется точно также, как и для целых частей числа, за тем лишь исключением, что разбивка на октавы и тетрады идёт вправо от десятичной запятой, недостающие разряды дополняются нулями справа. Например, рассмотренное выше число 1100,011₂ будет выглядеть как 14,3₈ или C,6₁₆.

7. Перевод из произвольной системы счисления в десятичную:

Точно также осуществляется перевод из любой системы счисления, только вместо «2» ставится основание системы.

12. Особенности целочисленной арифметики в эвм.

Однако целочисленная арифметика на ЭВМ имеет три очень существенных преимущества по сравнению с вещественной арифметикой:

• целые числа всегда представимы своими точными значениями;

• операции целочисленной арифметики дают точные результаты;

• операции целочисленной арифметики выполняются быстрее, чем операции вещественной («плавающей») арифметики.

Недостатком целого типа данных является сравнительно узкий диапазон допустимых значений (для типа Integer — от -32768 до 32767). При исполнении программы автоматически не контролируется выход значения целой величины за эти границы. В этом случае получается ошибочный результат. Если такая опасность существует, то программист должен сам предусматривать в своей программе предупреждение целочисленного переполнения. Чаще всего целый тип используется для представления счетчиков, номеров, индексов и других целочисленных величин.

Вещественный тип данных не является упорядоченным. Вещественные числа в памяти ЭВМ представляются в формате с плавающей точкой, т.е. в виде совокупности пары чисел — целого порядка и нормализованной мантиссы. Поскольку размер ячейки памяти ограничен, в большинстве случаев мантисса оказывается «обрезанной», иными словами, приближенной. Точное представление в памяти имеет лишь дискретное конечное множество вещественных значений.

13. Научная (экспоненциальная) форма записи числа. Машинное представление с плавающей точкой.

Экспоненциальная запись — представление действительных чисел в виде мантиссы и порядка. Удобна при представлении очень больших и очень малых чисел, а также для унификации их написания.

, где

• N — записываемое число;

• M — мантисса;

• n — основание показательной функции;

• p (целое) — порядок;

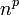•  — характеристика числа.

На компьютере (в частности в тексте компьютерных программ) экспоненциальную запись записывают в виде MEp, где:

M — мантисса,

E (exponent) — буква E, означающая «*10^» («…умножить на десять в степени…»).

p — порядок,

Например:

 (это элементарный заряд);

14. Различия представлений числовых и текстовых данных в ЭВМ.

15. Использование калькуляторов ОС UNIX (bc) и MS Windows для операций с числами в различных системах счисления.