
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Вариант 31
- •Вариант 32
Вариант 1
Тема: «Элементы векторной алгебры»
1. Даны точки
![]() и
и
![]() .
Найти:
.
Найти:
1) координаты и модуль вектора
![]() ;
;
2) скалярное произведение вектора
![]() и
и
![]() .
Будут ли эти векторы ортогональными?
.
Будут ли эти векторы ортогональными?
3) проекцию вектора
![]() на вектор
на вектор
![]() ;
;
4) координаты точки M,
делящей отрезок AB
в отношении
![]() .
.
2. Даны векторы
![]() ,
,
![]() и
и
![]() .
Найти:
.
Найти:
1) модуль векторного произведения
векторов
![]() и
и
![]() .
Будут ли векторы
и
коллинеарными?
.
Будут ли векторы
и
коллинеарными?
2) смешанное произведение векторов
![]() .
Будут ли эти векторы компланарными?
.
Будут ли эти векторы компланарными?
3) угол между векторами и .
3. Доказать, что векторы
![]() и
и
![]() образуют базис. Найти координаты вектора
образуют базис. Найти координаты вектора
![]() в этом базисе.
в этом базисе.
4. Найти собственные значения и собственные векторы матрицы A:
 .
.
Тема: «Приложения векторной алгебры в геометрии и физике»
1. К телу приложены три силы, которые
по модулю соответственно равны
![]() ,
,
![]() ,
,
![]() .
Сила
.
Сила
![]() составляет с горизонтальной осью угол
в
составляет с горизонтальной осью угол
в
![]() .
Найти:
.
Найти:
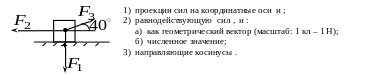
2. К точке
![]() приложены три силы
приложены три силы
![]() ,
,
![]() и
и
![]() .
Вычислить: 1) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
.
Вычислить: 1) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
![]() ;
;
2) модуль момента равнодействующей этих сил относительно точки B.
3. Вершины пирамиды находятся в
точках
![]() ,
,
![]() и
и
![]() .
Найти: 1) площадь сечения ABM,
где M
– середина DC;
2) объем пирамиды ABCD;
3) высоту пирамиды DH,
опущенную на грань ABC.
.
Найти: 1) площадь сечения ABM,
где M
– середина DC;
2) объем пирамиды ABCD;
3) высоту пирамиды DH,
опущенную на грань ABC.
Вариант 2
Тема: «Элементы векторной алгебры»
1. Даны точки
![]() и
и
![]() .
Найти:
.
Найти:
1) координаты и модуль вектора
![]() ;
;
2) скалярное произведение вектора и . Будут ли эти векторы ортогональными?
3) проекцию вектора на вектор ;
4) координаты точки M,
делящей отрезок AB
в отношении
![]() .
.
2. Даны векторы
![]() ,
,
![]() и
и
![]() .
Найти:
.
Найти:
1) модуль векторного произведения
векторов
![]() и
и
![]() .
Будут ли векторы
и
коллинеарными?
.
Будут ли векторы
и
коллинеарными?
2) смешанное произведение векторов . Будут ли эти векторы компланарными?
3) угол между векторами и .
3. Доказать, что векторы
![]() и
и
![]() образуют базис. Найти координаты вектора
образуют базис. Найти координаты вектора
![]() в этом базисе.
в этом базисе.
4. Найти собственные значения и собственные векторы матрицы A:
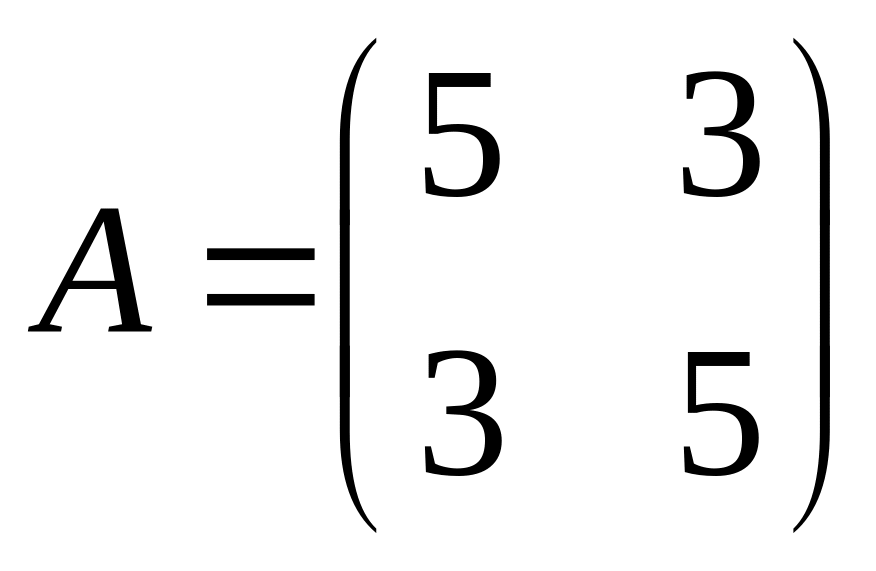 .
.
Тема: «Приложения векторной алгебры в геометрии и физике»
1. К телу приложены три силы, которые
по модулю соответственно равны
![]() ,
,
![]() ,
.
Сила
составляет с горизонтальной осью угол
в
,
.
Сила
составляет с горизонтальной осью угол
в
![]() .
Найти:
.
Найти:

2. К точке
![]() приложены три силы
приложены три силы
![]() ,
,
![]() и
и
![]() .
Вычислить: 1) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
;
.
Вычислить: 1) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
;
2) модуль момента равнодействующей этих сил относительно точки B.
3. Вершины пирамиды находятся в
точках
![]() ,
,
![]() и
и
![]() .
Найти: 1) площадь сечения ABM,
где M
– середина DC;
2) объем пирамиды ABCD;
3) высоту пирамиды DH,
опущенную на грань ABC.
.
Найти: 1) площадь сечения ABM,
где M
– середина DC;
2) объем пирамиды ABCD;
3) высоту пирамиды DH,
опущенную на грань ABC.
Вариант 3
Тема: «Элементы векторной алгебры»
1. Даны точки
![]() и
и
![]() .
Найти:
.
Найти:
1) координаты и модуль вектора
![]() ;
;
2) скалярное произведение вектора и . Будут ли эти векторы ортогональными?
3) проекцию вектора на вектор ;
4) координаты точки M,
делящей отрезок AB
в отношении
![]() .
.
2. Даны векторы
![]() ,
,
![]() и
и
![]() .
Найти:
.
Найти:
1) модуль векторного произведения
векторов
![]() и
и
![]() .
Будут ли векторы
и
коллинеарными?
.
Будут ли векторы
и
коллинеарными?
2) смешанное произведение векторов . Будут ли эти векторы компланарными?
3) угол между векторами и .
3. Доказать, что векторы
![]() и
и
![]() образуют базис. Найти координаты вектора
образуют базис. Найти координаты вектора
![]() в этом базисе.
в этом базисе.
4. Найти собственные значения и собственные векторы матрицы A:
 .
.
Тема: «Приложения векторной алгебры в геометрии и физике»
1. К телу приложены три силы, которые
по модулю соответственно равны
![]() ,
,
,
,
![]() .
Сила
составляет с горизонтальной осью угол
в
.
Сила
составляет с горизонтальной осью угол
в
![]() .
Найти:
.
Найти:

2. К точке
![]() приложены три силы
приложены три силы
![]() ,
,
![]() и
и
![]() .
Вычислить: 1) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
;
.
Вычислить: 1) работу, производимую
равнодействующей этих сил, когда точка
ее приложения, двигаясь прямолинейно,
перемещается в точку
;
2) модуль момента равнодействующей этих сил относительно точки B.
3. Вершины пирамиды находятся в
точках
![]() ,
,
![]() и
и
![]() .
Найти: 1) площадь сечения ABM,
где M
– середина DC;
2) объем пирамиды ABCD;
3) высоту пирамиды DH,
опущенную на грань ABC.
.
Найти: 1) площадь сечения ABM,
где M
– середина DC;
2) объем пирамиды ABCD;
3) высоту пирамиды DH,
опущенную на грань ABC.
