
- •1 Основні поняття теорії похибок
- •1.1 Поняття похибки
- •1.2 Дії над наближеними числами
- •1.3 Пряма та обернена задачі теорії похибок
- •1.3 Джерела похибок обчислень
- •2 Обчислення значень функцій
- •2.1 Обчислення значень полінома. Схема Горнера
- •2.2 Наближене знаходження сум числових рядів
- •2.3 Обчислення значень аналітичної функції
- •2.4 Обчислення значень показової функції
- •2.5 Обчислення значень логарифмічної функції
- •2.6 Обчислення значень тригонометричних функцій
- •3 Розв’язування систем лінійних алгебраїчних рівнянь (слар)
- •3.1 Концепція методів
- •3.2 Метод простої ітерації
- •3.3 Метод Гаусса-Зейделя
- •4 Розв’язування нелінійних алгебраїчних та трансцендентних рівнянь
- •1. Етап відділення кореня: на цьому етапі відділяється корінь, тобто знаходиться такий відрізок, усередині якого міститься точно один корінь і з цього відрізка береться початкове наближення кореня.
- •2. Етап уточнення кореня: на цьому етапі послідовно уточнюють корінь, тобто знаходять значення із заданою точністю .
- •4.1 Відділення коренів
- •4.2 Метод половинного поділу (метод дихотомії)
- •4.3 Метод хорд (спосіб пропорційних частин)
- •4.4 Метод Ньютона (метод дотичних)
- •4.5 Комбінований метод
- •4.6 Метод ітерації
- •4.7 Метод ітерації для системи двох рівнянь
- •5 Обробка емпіричних даних
- •5.1 Інтерполяція та екстраполяція
- •5.2 Концепція інтерполяції та екстраполяції
- •5.3 Лінійна і квадратична локальні інтерполяції
- •5.4 Глобальна інтерполяція. Многочлен Лагранжа
- •5.5 Глобальна інтерполяція. Многочлен Ньютона
- •5.6 Апроксимація
- •При цьому вимагається, щоб
- •Побудуємо емпіричний точковий графік.
- •Візуальний аналіз побудови дозволяє обрати на роль апроксимуючої функції квадратичну параболу
- •6 Наближене обчислення визначених інтегралів
- •6.1 Концепція чисельного інтегрування
- •6.2 Методи прямокутників та трапецій
- •6.3 Метод Симпсона
- •6.4 Метод Монте-Карло
2 Обчислення значень функцій
При обчисленні за допомогою комп’ютерів значень функцій, заданих формулами, далеко не байдуже, у якому вигляді записана відповідна формула. Математично еквівалентні вирази часто виявляються нерівноцінними з погляду наближених обчислень. Тому виникає практично важлива задача про знаходження для елементарних функцій найбільш зручних аналітичних виразів. Обчислення значень функцій звичайно зводиться до послідовності елементарних арифметичних дій. З огляду на обмеженість об’єму пам’яті комп’ютера, бажано ці операції розбивати на повторювані цикли. Нижче ми розглянемо деякі типові прийоми обчислень.
2.1 Обчислення значень полінома. Схема Горнера
Нехай
задано поліном
![]() -го
степеня
-го
степеня
![]() (2.1)
(2.1)
з
дійсними коефіцієнтами
![]() .
Нехай потрібно знайти значення цього
полінома при
.
Нехай потрібно знайти значення цього
полінома при
![]() (грецька
буква «ксі»):
(грецька
буква «ксі»):
![]() .
(2.2)
.
(2.2)
Обчислення
числа
![]() зручніше за все робити в такий спосіб.
Представимо формулу (2.2) у вигляді:
зручніше за все робити в такий спосіб.
Представимо формулу (2.2) у вигляді:
![]() .
.
Звідси, послідовно обчислюючи числа
![]() (2.3)
(2.3)
знаходимо
![]() .
.
Неважко
довести (спробуйте це зробити самостійно),
що числа
![]() є коефіцієнтами полінома
є коефіцієнтами полінома
![]() ,
отриманого як частку при діленні даного
полінома
,
отриманого як частку при діленні даного
полінома
![]() на
двочлен
на
двочлен
![]() .
.
Таким
чином, формули (2.3) дозволяють, не виконуючи
ділення, визначати коефіцієнти частки
![]() ,
а
також остачу
.
Практично обчислення здійснюються за
наступною схемою, яка називається схемою
Горнера:
,
а
також остачу
.
Практично обчислення здійснюються за
наступною схемою, яка називається схемою
Горнера:
![]()
![]()
Приклад 1. Обчислити значення полінома
![]() при
при
![]() .
.
Розв’язок. Складемо схему Горнера:
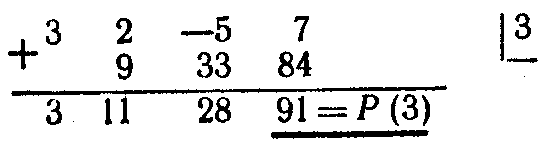
Зауваження.
Користуючись схемою Горнера, можна
одержати границі дійсних коренів даного
полінома
![]() .
.
Припустимо,
що при
![]() всі коефіцієнти
всі коефіцієнти
![]() в схемі Горнера невід’ємні, причому
перший коефіцієнт додатний, тобто
в схемі Горнера невід’ємні, причому
перший коефіцієнт додатний, тобто
![]() (2.4)
(2.4)
Тоді
можна стверджувати, що всі дійсні корені
![]() полінома
розташовані не правіше
полінома
розташовані не правіше
![]() ,
тобто
,
тобто
![]() (рис. 2.1).
(рис. 2.1).
![]()
Рис. 2.1
Справді, тому що
![]() ,
,
то
при кожному
![]() в силу умови (2.4) будемо мати
в силу умови (2.4) будемо мати
![]() ,
тобто
будь-яке число, більше
,
завідомо не є коренем полінома
.
Таким
чином, маємо верхню оцінку для дійсних
коренів
,
тобто
будь-яке число, більше
,
завідомо не є коренем полінома
.
Таким
чином, маємо верхню оцінку для дійсних
коренів
![]() полінома.
полінома.
Для одержання нижньої оцінки коренів складемо поліном
![]() .
.
Для
цього нового полінома знаходимо таке
число
![]() ,
щоб всі коефіцієнти у відповідній
схемі Горнера були невід’ємні, за
винятком першого, котрий, очевидно,
буде додатним. Тоді відповідно до
попередніх міркувань для дійсних коренів
полінома
,
щоб всі коефіцієнти у відповідній
схемі Горнера були невід’ємні, за
винятком першого, котрий, очевидно,
буде додатним. Тоді відповідно до
попередніх міркувань для дійсних коренів
полінома![]() ,
очевидно,
рівних
,
очевидно,
рівних
![]() ,
маємо
нерівність
,
маємо
нерівність
![]() .
.
Отже,
![]() .
Таким чином, ми одержали нижню границю
.
Таким чином, ми одержали нижню границю
![]() дійсних коренів полінома
.
Звідси
випливає, що всі дійсні корені полінома
розташовані
на відрізку
дійсних коренів полінома
.
Звідси
випливає, що всі дійсні корені полінома
розташовані
на відрізку
![]() .
.
Приклад 2. Знайти границі дійсних коренів полінома
![]() .
.
Розв’язок.
Підрахуємо значення полінома
,
наприклад, при
![]() .
Користуючись
схемою Горнера, одержимо:
.
Користуючись
схемою Горнера, одержимо:
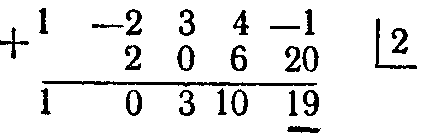
Тому
що всі коефіцієнти
![]() ,
то дійсні корені
полінома
(якщо
вони існують) задовольняють нерівності
,
то дійсні корені
полінома
(якщо
вони існують) задовольняють нерівності
![]() .
Верхня границя дійсних коренів знайдена.
Перейдемо до оцінки нижньої границі.
Складемо новий поліном:
.
Верхня границя дійсних коренів знайдена.
Перейдемо до оцінки нижньої границі.
Складемо новий поліном:
![]() .
.
Підраховуючи
значення полінома
,
наприклад, при
![]() ,
маємо:
,
маємо:
![]()
Всі
коефіцієнти
,
виходить,
![]() .
.
Отже,
всі дійсні корені даного полінома
перебувають усередині відрізка
![]() .
.
