4.5 Комбінований метод

Нехай , і зберігають сталі знаки на відрізку . Об’єднуючи методи хорд та Ньютона, отримаємо метод, на кожному етапі якого знаходимо значення з нестачею та значення з надлишком точного кореня рівняння .

Звідси, зокрема, випливає, що цифри, спільні для і , обов’язково належать точному кореню . Теоретично можливі чотири випадки:

1) (мал. 4.7);

2) (мал. 4.8);

3) (мал. 4.9);

4) (мал. 4.10 ).

Ми обмежимося розглядом першого випадку. Інші випадки вивчаються аналогічно, причому характер обчислень легко зрозуміти з відповідних малюнків. Зауважимо, що ці випадки можна звести до першого, якщо замінити досліджуване рівняння рівносильними йому рівняннями: та , де .

Отже, нехай та при . Покладемо та

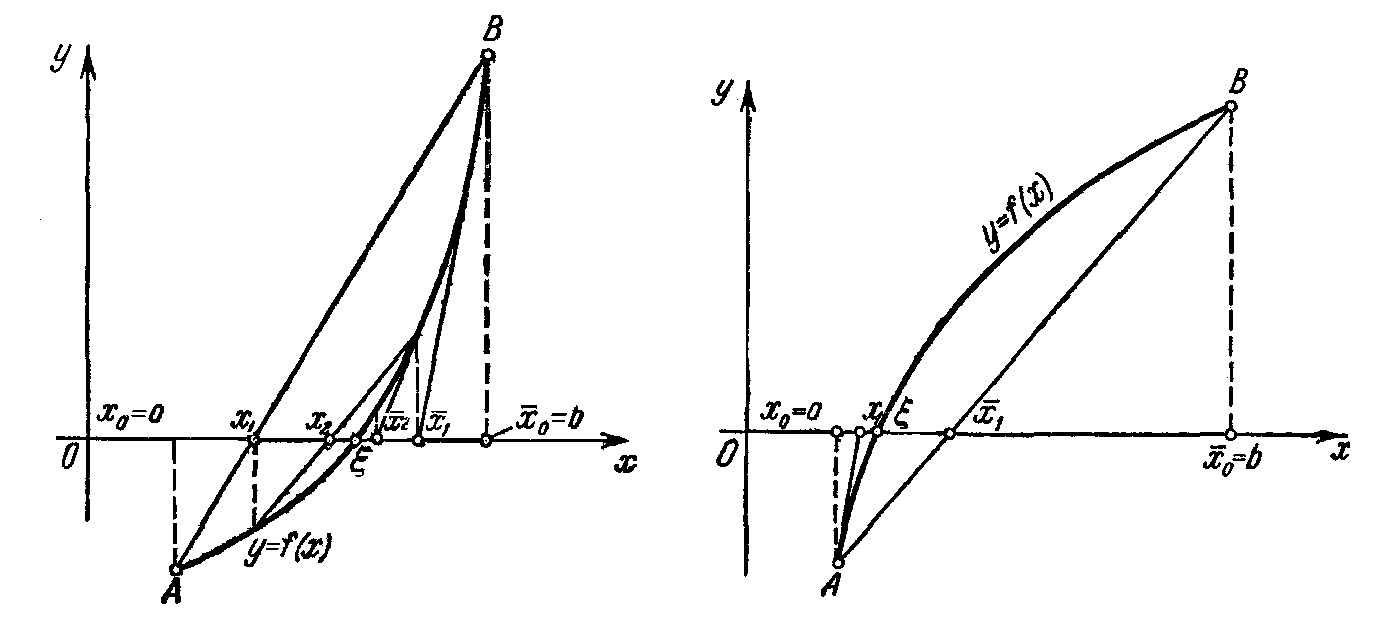
Рис. 4.7 Рис. 4.8

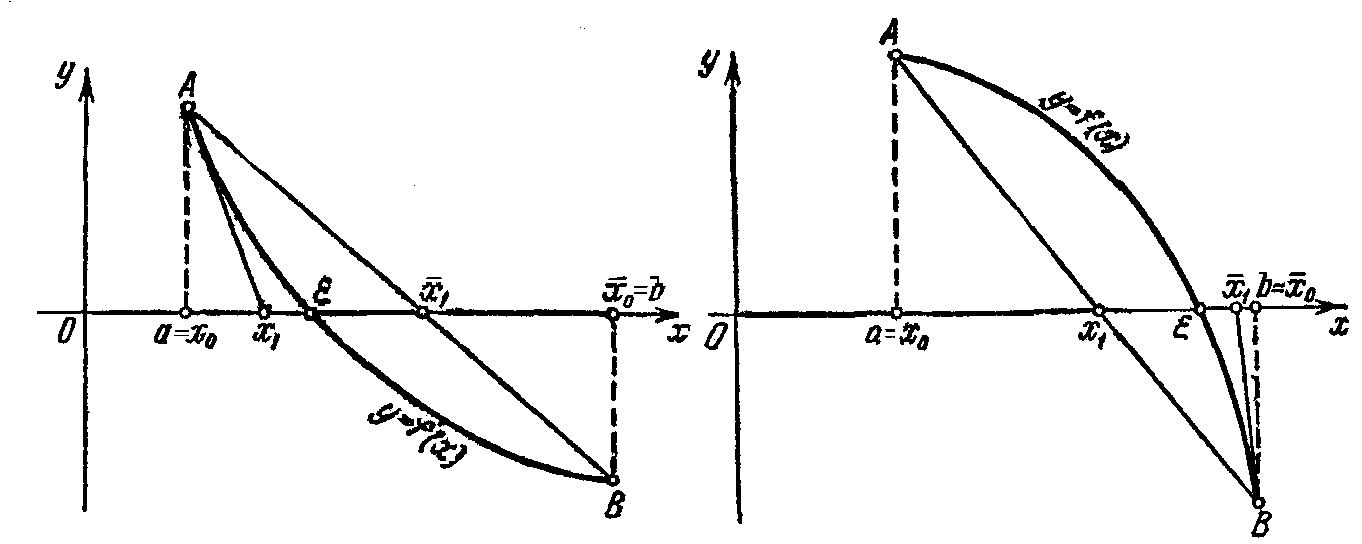
Рис. 4.9 Рис. 4.10

У формулах та метод хорд застосовується на кожному кроці до нового відрізка .

Легко встановити, що

(4.18).

Отже, якщо абсолютна похибка наближеного кореня задана попередньо і рівна , то процес зближення закінчується тоді, коли буде встановлено, що . По закінченню процесу значення кореня краще всього прийняти рівним середньому арифметичному знайдених останніх значень:

.

Приклад. Обчислити з точністю єдиний додатний корінь рівняння

.

Розв’язок. Так як і , то корінь знаходиться в інтервалі . Маємо:

та .

У вибраному нами інтервалі перша та друга похідні зберігають додатний знак.

Застосуємо комбінований метод, поклавши та .

Обчислення за формулами та дадуть такі результати:

.

Так як , обчислення потрібно продовжити. Знаходимо наступну пару наближень:

.

Так як , обчислення слід закінчити.

Можна покласти:

.

4.6 Метод ітерації

Одним з найбільш важливих методів чисельного розв’язування рівнянь є метод ітерації ( часто метод ітерації називають методом послідовних наближень). Сутність цього методу полягає у наступному.

Нехай дано рівняння

(4.19),

де — неперервна функція, і потрібно знайти його дійсні корені.

Замінимо рівняння (4.19) рівносильним рівнянням

. (4.20)

Виберемо яким-небудь способом наближене значення кореня та підставимо його у праву частину рівняння (4.20). Тоді отримаємо деяке число

. (4.21)

Підставимо тепер у праву частину рівності (4.20) замість число , отримаємо нове число . Повторюючи цей процес, отримаємо послідовність чисел

. (4.22)

Якщо ця послідовність — збіжна, тобто існує границя , то, переходячи до границі у рівності (4.22) и вважаючи функцію неперервною, знаходимо:

або

(4.23).

Таким чином, границя є коренем рівняння (4.20) и може бути обчислена за формулою (4.22) з будь-якою точністю.

Для практичного застосування методу ітерації потрібно з’ясувати достатні умови збіжності ітераційного процесу.

Теорема 1 (без доведення). Нехай функція визначена і диференційована на відрізку , причому всі її значення .

Тоді, якщо існує дійсне число таке, що

(4.24)

при , то:

1) процес ітерації

збігається незалежно від початкового значення ;

2) граничне значення

є єдиним коренем рівняння

.

Зауваження 1. Теорема залишається справедливою, якщо функція визначена та диференційована на нескінченому інтервалі , причому при виконується нерівність (4.24).

Зауваження 2. В умовах теореми 1 метод ітерації збігається при будь-якому виборі початкового значення . Завдяки цьому цей метод є таким, що сам виправляється, тобто, окрема помилка у обчисленнях, яка не виводить за межі відрізка , не вплине на кінцевий результат, адже помилкове значення можна розглядувати як нове початкове значення . Можливо, зросте лише обсяг роботи. Властивість самовиправлення робить метод ітерації одним з надійніших методів обчислення. Звичайно, систематичні помилки при застосуванні методу ітерації можуть завадити отриманню правильного результату.

Оцінка наближення. Процес ітерації слід продовжувати до тих пір, доки для двох послідовних наближений і не буде забезпечено виконання нерівності

,

де - задана похибка кореня і .

Якщо , то з нерівності випливає нерівність .

Приклад. Знайти з точністю один з коренів рівняння .

Розв’язок.

. Дане рівняння має корінь на інтервалі .

Представимо рівняння у вигляді . У цьому випадку .

Очевидно, що при маємо також .

Похідна .

При маємо .

Умови теореми 1 виконані. Процес ітерації будемо здійснювати до забезпечення виконання нерівності

.

Покладемо . Послідовно обчислюємо:

На цьому процес ітерації можна зупинити, так як .

Покладемо .

Приклад 2. Знайти методом ітерацій найбільший додатний корінь рівняння з точністю .

Розв’язок. Легко впевнитися в тому, що шуканий корінь знаходиться на інтервалі . Справді, і при .

Початкове рівняння можна переписати у вигляді , або , або тощо.

Найвигіднішим серед цих способів є останній, так як, обравши за основний проміжок і поклавши

,

знайдемо, що похідна

за абсолютною величиною не перевищує :

.

Розраховуємо послідовні наближення з одним запасним знаком за формулою

Так як , то з точністю можна покласти

Приклад 3. Рівняння

Має корінь , так як та .

Дане рівняння можна записати у вигляді

.

Тут

та ;

тому при .

Отже, умови збіжності процесу ітерації не виконуються.

Якщо записати початкове рівняння у вигляді

,

то матимемо

та .

Звідси при , отже, процес ітерації є збіжним.