
- •Случайные величины и их числовые характеристики Вариант I
- •Случайные величины и их числовые характеристики Вариант 2.
- •Случайные величины и их числовые характеристики Вариант 3
- •Случайные величины и их числовые характеристики Вариант 4
- •Случайные величины и их числовые характеристики Вариант 5
- •Типовой расчет Случайные величины и их числовые характеристики Вариант 6
- •Типовой расчет Случайные величины и их числовые характеристики Вариант 7
- •Задана плотность распределения системы двух случайных величин . Найдите коэффициент и коэффициент корреляции .
- •Типовой расчет Случайные величины и их числовые характеристики Вариант 8
- •Типовой расчет Случайные величины и их числовые характеристики Вариант 9
- •Задана плотность распределения системы двух случайных величин . Найдите коэффициент и коэффициент корреляции .
- •Типовой расчет Случайные величины и их числовые характеристики Вариант 12
- •Задан ряд распределения случайной величины . Найдите математическое ожидание, дисперсию и среднее квадратическое отклонение. Постройте функцию распределения.
- •Закон распределения системы дискретных случайных величин задан таблицей. Найдите коэффициент корреляции и вероятность попадания случайной величины в область .
- •Типовой расчет Случайные величины и их числовые характеристики Вариант 13
- •Типовой расчет Случайные величины и их числовые характеристики Вариант 14
- •Закон распределения системы дискретных случайных величин задан таблицей. Найдите коэффициент корреляции и вероятность попадания случайной величины в область .
- •Типовой расчет Случайные величины и их числовые характеристики Вариант15
- •Типовой расчет Случайные величины и их числовые характеристики Вариант 16
- •Закон распределения системы дискретных случайных величин задан таблицей. Найдите коэффициент корреляции и вероятность попадания случайной величины в область .
- •Задана плотность распределения системы двух случайных величин . Найдите коэффициент и коэффициент корреляции .
- •Типовой расчет Случайные величины и их числовые характеристики Вариант 17
- •Задан ряд распределения случайной величины . Найдите математическое ожидание, дисперсию и среднее квадратическое отклонение. Постройте функцию распределения.
- •Для непрерывной случайной величины задана плотность распределения . Требуется найти параметр , функцию распределения , математическое ожидание, дисперсию, среднее квадратическое отклонение.
- •Закон распределения системы дискретных случайных величин задан таблицей. Найдите коэффициент корреляции и вероятность попадания случайной величины в область .
- •Задана плотность распределения системы двух случайных величин . Найдите коэффициент и коэффициент корреляции .
Божко А. Типовой расчет
Случайные величины и их числовые характеристики Вариант I
Мяч бросается в корзину до первого попадания, но число бросков не больше 6. Составьте ряд распределения числа бросков, если вероятность попадания при каждом броске мяча в корзину
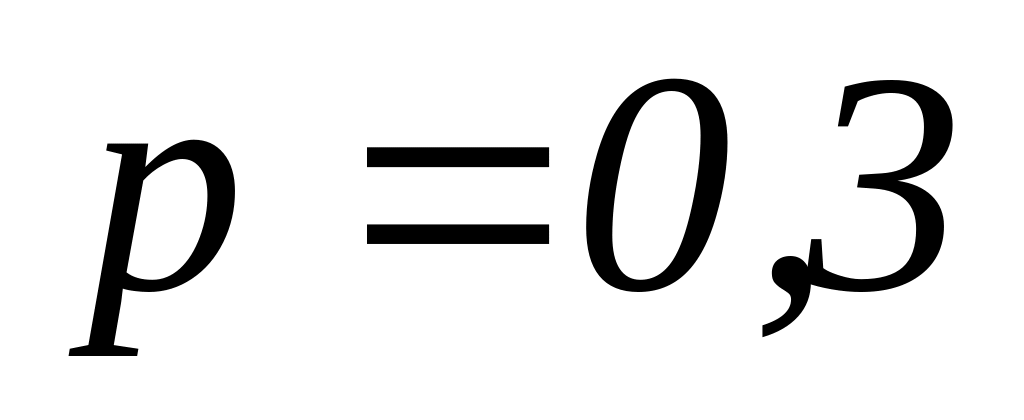 .
.Задан ряд распределения случайной величины
 .
Найдите математическое ожидание,
дисперсию и среднее квадратическое
отклонение. Постройте функцию
распределения.
.
Найдите математическое ожидание,
дисперсию и среднее квадратическое
отклонение. Постройте функцию
распределения.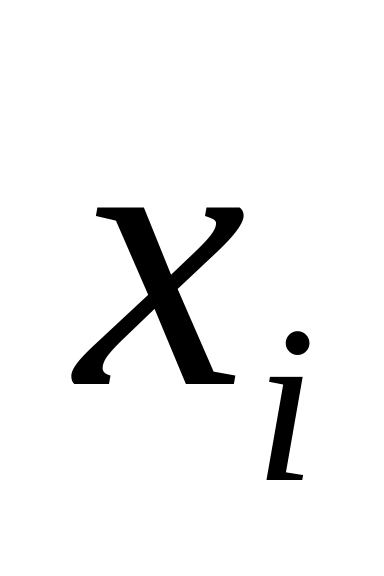
3
5
7
9
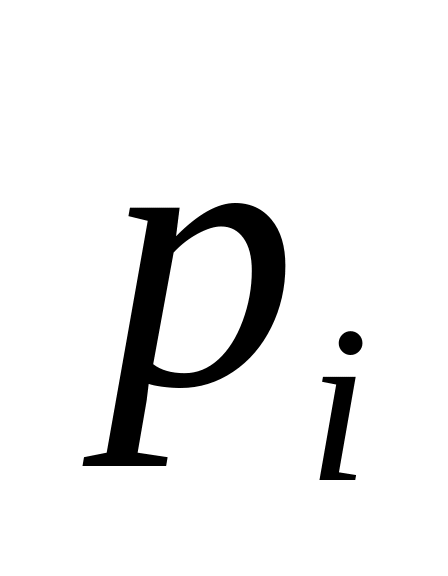
0,3
0,4
0,2
0,1
Для непрерывной случайной величины задана функция распределения
 .
Найдите плотность распределения
.
Найдите плотность распределения
 ,
математическое ожидание, дисперсию,
среднее квадратическое отклонение.
Вычислите вероятность того, что
отклонение случайной величины от ее
математического ожидания будет не
более среднего квадратического
отклонения. Постройте графики функций
и
.
,
математическое ожидание, дисперсию,
среднее квадратическое отклонение.
Вычислите вероятность того, что
отклонение случайной величины от ее
математического ожидания будет не
более среднего квадратического
отклонения. Постройте графики функций
и
.
![]()
Для непрерывной случайной величины задана плотность распределения . Требуется найти параметр
 ,
функцию распределения
,
математическое ожидание, дисперсию,
среднее квадратическое отклонение.
,
функцию распределения
,
математическое ожидание, дисперсию,
среднее квадратическое отклонение.
ƒ(x)
a
-2
0
4
x
Случайное отклонение размера детали от номинала распределено по нормальному закону с параметрами и
 .
Стандартными являются те детали, для
которых отклонения от номинала лежат
в интервале
.
Стандартными являются те детали, для
которых отклонения от номинала лежат
в интервале
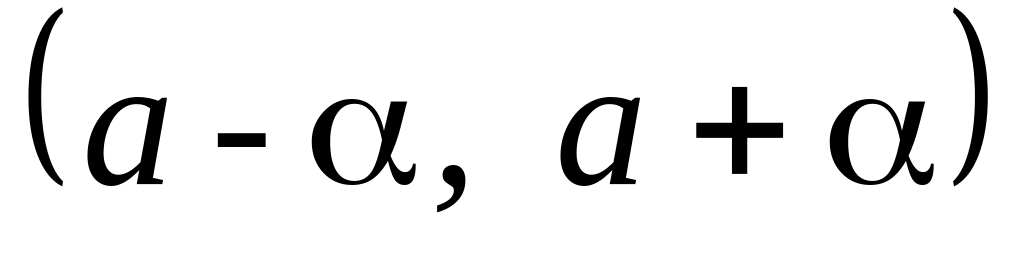 .
Запишите формулу плотности распределения
и постройте график плотности распределения.
.
Запишите формулу плотности распределения
и постройте график плотности распределения.
Сколько необходимо изготовить деталей,
чтобы с вероятностью не менее
![]() среди них была хотя бы одна стандартная?
среди них была хотя бы одна стандартная?
![]() .
.
З
акон распределения системы дискретных случайных величин 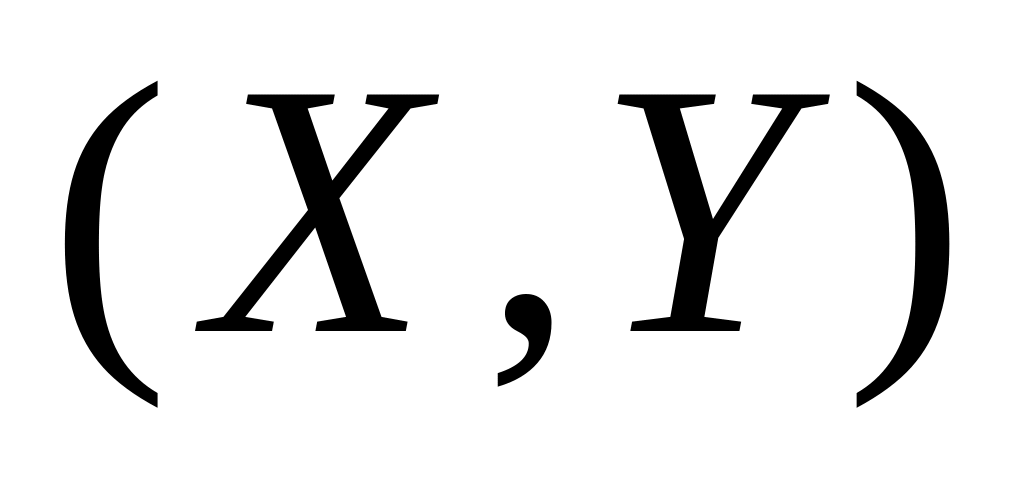 задан
таблицей. Найдите коэффициент корреляции
задан
таблицей. Найдите коэффициент корреляции
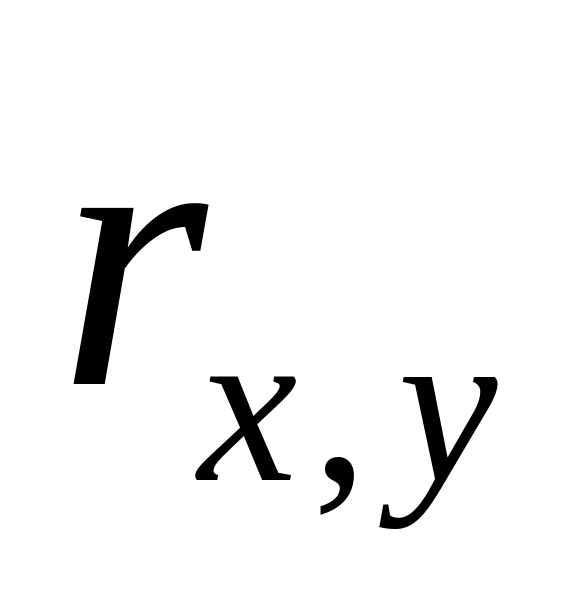 и вероятность попадания случайной
величины
в
область
и вероятность попадания случайной
величины
в
область
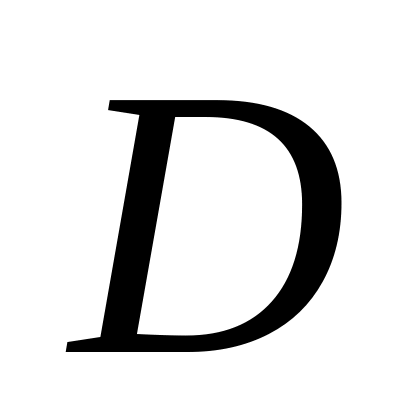
 .
.Y X
1
2
3
4
-2
0,03
0,02
0,06
0,04
0
0,03
0,1
0,1
0,09
2
0,05
0,08
0,2
0,2
Задана плотность распределения
 системы двух случайных величин
системы двух случайных величин
 .
Найдите коэффициент
.
Найдите коэффициент
 и коэффициент корреляции
и коэффициент корреляции
 .
.
![]()
![]() .
.
Среднее значение длины детали равно 50 см, а дисперсия равна 0,1. Пользуясь неравенством Чебышева, оцените вероятность того, что приготовленная деталь окажется по своей длине не менее 49,5 и не более 50,5 см.
Случайные величины и
 независимы:
независимы:
![]()
![]()
Найдите M(![]() ),
M(
),
M(![]() ),
D(
),
D(![]() ),
D(
),
D(![]() ).
).
Зайдуллина Г. Типовой расчет
Случайные величины и их числовые характеристики Вариант 2.
Опыт состоит из трех независимых бросаний монеты, при каждом из которых вероятность выпадения герба
 .
Составьте ряд распределения числа
появлений герба.
.
Составьте ряд распределения числа
появлений герба.Задан ряд распределения случайной величины . Найдите математическое ожидание, дисперсию и среднее квадратическое отклонение. Постройте функцию распределения.
1
2
5
7
0,1
0,2
0,4
0,3
Для непрерывной случайной величины задана функция распределения . Найдите плотность распределения , математическое ожидание, дисперсию, среднее квадратическое отклонение. Вычислите вероятность того, что отклонение случайной величины от ее математического ожидания будет не более среднего квадратического отклонения. Постройте графики функций и .
![]()
Для непрерывной случайной величины задана плотность распределения
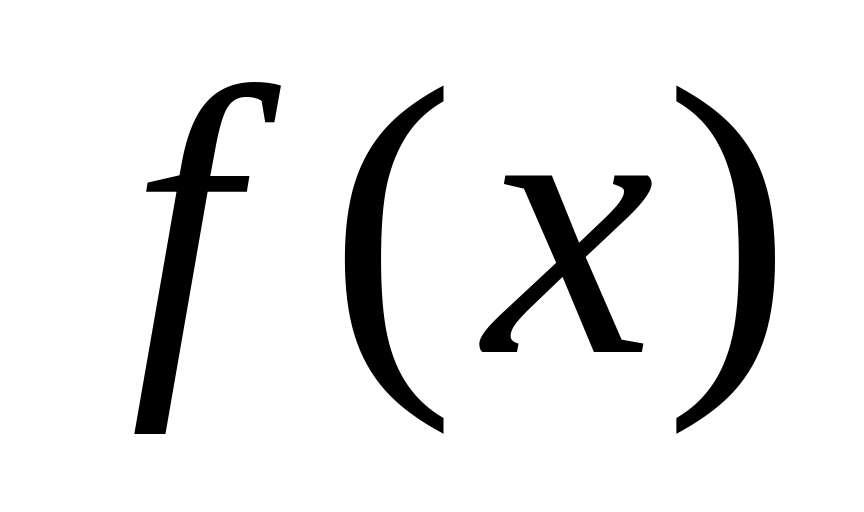 .
Требуется найти параметр
,
функцию распределения
.
Требуется найти параметр
,
функцию распределения
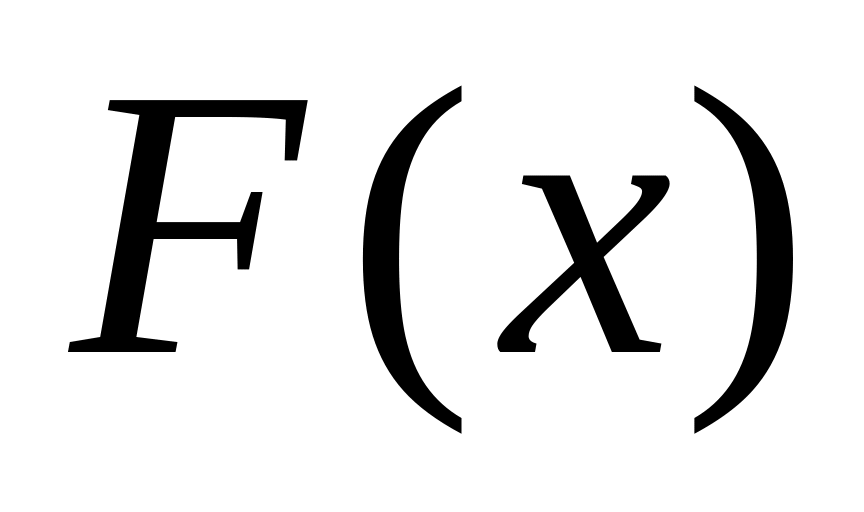 ,
математическое ожидание, дисперсию,
среднеквадратическое отклонение.
,
математическое ожидание, дисперсию,
среднеквадратическое отклонение.
![]()
Случайное отклонение размера детали от номинала распределено по нормальному закону с параметрами и . Стандартными являются те детали, для которых отклонения от номинала лежат в интервале . Запишите формулу плотности распределения и постройте график плотности распределения.
Сколько необходимо изготовить деталей, чтобы с вероятностью не менее среди них была хотя бы одна стандартная?
![]() .
.
Закон распределения системы дискретных случайных величин задан таблицей. Найдите коэффициент корреляции и вероятность попадания случайной величины в область
![]() .
.
X Y |
-2 |
-1 |
0 |
1 |
-1 |
0,02 |
0,05 |
0,04 |
0,1 |
0 |
0,03 |
0,08 |
0,05 |
0,2 |
2 |
0,02 |
0,05 |
0,06 |
0,3 |
Задана плотность распределения системы двух случайных величин . Найдите коэффициент и коэффициент корреляции .
![]()
![]() .
.
Пусть всхожесть семян некоторой культуры равна 0,75. Пользуясь неравенством Чебышева, оцените вероятность того, что из посеянных 1000 семян число взошедших окажется от 700 до 800 включительно.
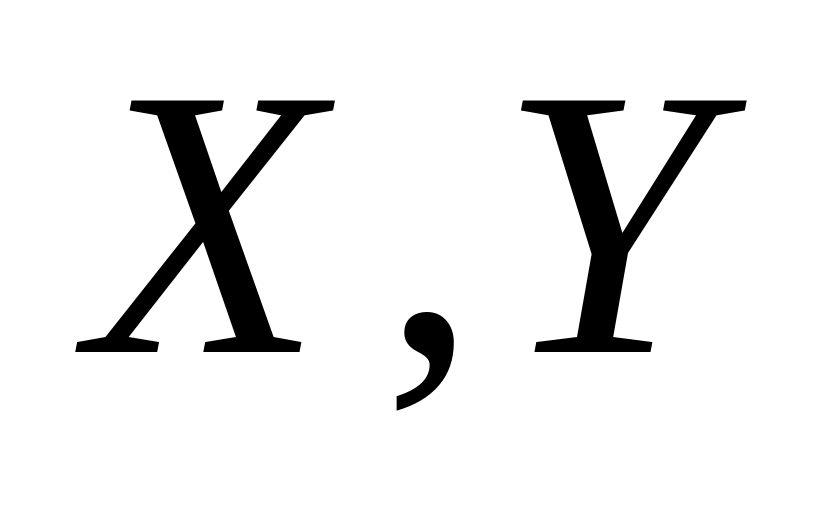 — независимые случайные
величины:
— независимые случайные
величины:
![]()
![]()
Найдите:![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
Ишметьева Е. Типовой расчет
