Тема 5: Принцип двоїстості.

Мета: дати поняття принципу двоїстості; показати використання принципу двоїстості при доведенні теорем( напр. теореми Дезарга).

План

1.Властивості відображення точок проективної площини на множину прямих цієї площини.

2. Принцип двоїстості на площині.

3. Принцип двоїстості у просторі.

4.Теорема Дезарга.

Ключові слова : ін’єктивне, бієктивне відображення ,принцип двоїстості, , пучок прямих, “точка лежить на”,” пряма проходить через”, теорема Дезарга, двоїсті образи прямої, точок прямої, пучка прямих .

Принцип двоїстості

P V , R P

Позначимо P* - множину всіх прямих площини P

f : P P* , M P

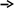M m P* M(m , m , m ) m: х m + х m + х m =0

1) f-ін’єктивне:

M, N P , f(M) = m: m х + m х + m х =0 P*

f(N) = n: n х + n х + n х =0 P*

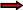
M N (m , m , m ) (n , n , n ) m n

2 ) f-сюр’єктивне:

m P*, m: m х + m х + m х =0

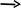M(m , m , m ) M m

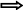
(1),( 2) f --бієктивне f : P* P - бієктивне

При f, f зберігається взаємна належність точок і прямих

Нехай: А, В, С d

f f f f ^-1

A a В b С c d D

A _R d : d₁x₁₊ d₂x₂₊ d₃x₃=0._R Якщо А d

d₁а₁₊ d₂а₂₊ d₃а₃=0

Але

A D D(d₁,d₂.d₃) a

B

C

d a b c

Тому, якщо А, В, С d

О тже, образом точок прямої при відображені f є пучок прямих, а при відображені образом пучка прямих є точки прямої

Принцип двоїстості на площині

Якщо справедливе твердження, у якому йде мова про точки, прямі та відношення належності між ними, то буде справедливе і твердження,

яке отримується такою заміною слів

т очка, пряма, лежить на, проходить через

пряма, точка ,проходить через, лежить на

Принцип двоїстості у просторі

Якщо справедливе твердження, у якому йде мова про точки, прямі, площини та відношення між ними, то буде справедливе і твердження,

які отримується такою заміною слів

т очка, пряма, площина, лежить на, проходить через

площина, пряма, точка проходить через, лежить на