§ 7.5. Дифференцирование функций, заданных параметрически
Если
,
то производная имеет вид
.
Доказательство.
.
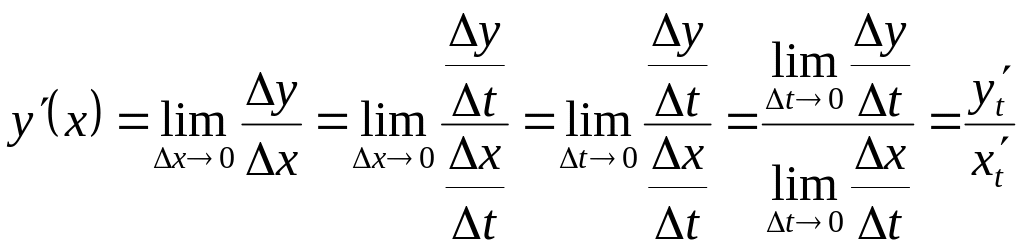Пример.
,
,
,
.
Примеры для самостоятельного решения
Определить
7.21.
,
7.22.
7.23.
.
§ 7.6. Первый дифференциал функции, инвариантность его формы
Как уже говорилось выше,
.
Теорема. Форма записи дифференциала (первого дифференциала) функции не отличается для случаев независимой и зависимой переменной, то есть инвариантна.
Доказательство.
Пусть
- сложная функция, причем
независимая
переменная,
зависящая
от
переменная. В соответствии с только что
введенной формулой для дифференциала
имеем
,
но
является сложной функцией и при вычислении
производной это следует учесть. Поскольку
,
,
а подчеркнутые члены представляют собой
дифференциал функции
,
естественно, можно записать
.
Итак, дифференциал функции можно
представить двумя формулами
и
,
причем
независимая,
а
зависимая
переменные. Нетрудно заметить, что форма
записи дифференциала одинакова, то есть
инвариантна.
Это свойство первого дифференциала функции лежит в основе интегрирования.
Пример.
,
.
§ 7.7. Производные и дифференциалы высших порядков
В математике широко используются производные функции высших порядков. Это оправдывается хотя бы тем, что физический смысл второй производной представляет собой ускорение тела. В самом деле, если вторую производную функции ввести как производную от производной, то есть
,
и учесть, что физический смысл первой производной есть скорость, то вторая производная, очевидно, показывает скорость изменения этой скорости, то есть ускорение.
Аналогично можно
ввести понятия третьей, четвертой и так
далее производных:
,
…..
За редким исключением производные высших порядков вычисляются последовательно, то есть для получения пятой производной необходимо вначале найти первую, затем вторую, третью и четвертую производные, и после этого пятую производную.
Пример 1.
,
,
,
…
На примере 1 было показано, как находить старшие производные для явно заданной функции.
Пример 2. Вычислим вторую производную неявной функции
Определим вначале
первую производную, дифференцируя обе
части равенства по
,
или
.
Дифференцируем полученное уравнение еще раз
,
тогда
.
После приведения подобных членов
определяем
.
Из полученного
выражения можно исключить первую
производную, которую определим из ранее
полученного уравнения
,
после приведения подобных членов
тогда
.
Примеры для самостоятельного решения
Вычислить
7.24.
,
7.25.
.
Определим вторую производную для параметрически заданной функции, для чего выведем необходимую для этого формулу. Ранее была получена формула для первой производной функции , которая имела вид . Дифференцируем обе части равенства по , тогда
.
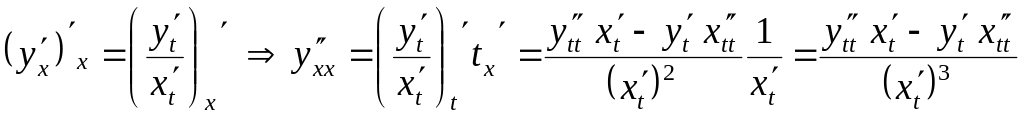Итак,
.
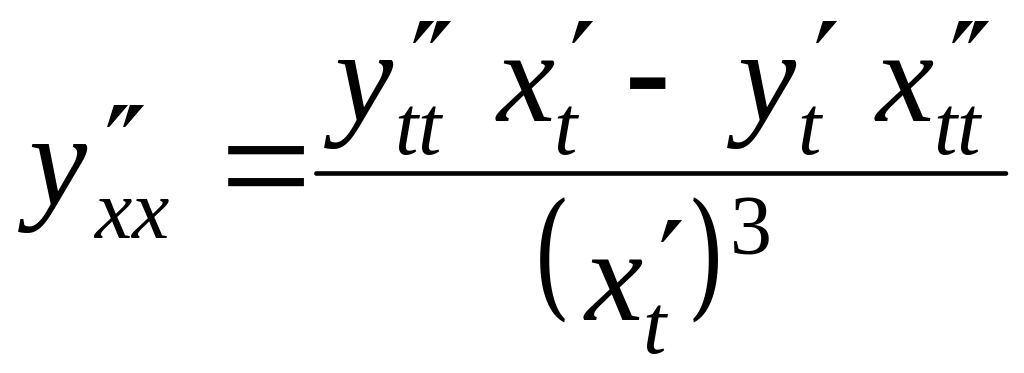Пример. Дана
функция
.
Определить
.
В соответствии с полученной формулой находим
,
,
,
,
Очевидно,
.
Примеры для самостоятельного решения
Вычислить
7.26.
, 7.27.
,
7.28.
.
Дифференциалы высших порядков
По аналогии с
производными введем понятие дифференциала
второго порядка, обозначив его
:
.
Этот дифференциал не обладает инвариантностью формы записи. Покажем это. Очевидно,
.
Если функция
простая, то есть,
независимая
переменная, то аргумент
и его приращение
никак не связаны между собой, другими
словами
может быть любым числом из области
существования функции
тоже, следовательно,
при дифференцировании по
ведет себя как постоянная тогда
.
Когда функция
сложная
,
имеется связь между ее промежуточным
аргументом
и его приращением
поскольку и
,
и
зависят от
.
В выражении для производной, а
следовательно, и дифференциала появляется
второе слагаемое
.
Еще больше дополнительных членов появляется в третьем дифференциале сложной функции и так далее.