§ 7.4. Производные неявно заданных функций
Дифференцировать неявные функции можно по тем же правилам, что явные, однако, при этом необходимо договориться, что при этом задании является функцией, а что аргументом. Иначе сама постановка задачи теряет смысл. Возможны два пути решения задачи. Первый – от неявного задания функции перейти к явному, если это возможно. Второй – дифференцировать непосредственно заданную функцию.
Рассмотрим несколько примеров.
1)
Видим, что уравнением задана неявная
функция, а также, что при этом задании
предлагается считать
функцией,
а
аргументом
и вычислять производную от функции
по аргументу
.
1 способ (он здесь
возможен). Определяем из уравнения
,
тогда
.
2 способ. Дифференцируем
обе части уравнения
по аргументу
:
.
При раскрытии этого выражения следует
учесть, что при дифференцировании по
первое слагаемое левой части уравнения
является простой функцией, а производную
от второго слагаемого следует искать
как производную сложной функции с
промежуточным аргументом
.
Итак,
( напомним, что
производную от степенной функции следует
умножить на производную промежуточного
аргумента
).
2)
.
В этом случае первый способ дифференцирования неприменим, поскольку решить данное уравнение невозможно ни относительно , ни относительно .
Поскольку с выбором функции (это опять ) определились при постановке задачи, дифференцируем обе части равенства по аргументу :
.
Очевидно,
.
Приведем подобные члены, собрав все слагаемы с в левой части равенства.
.
Определяем отсюда производную
.
Примеры для самостоятельного решения
Определить .
7.10.
,
7.11.
,
7.12.
,
7.13.
,
7.14.
,
7.15.
.
"Логарифмическое" дифференцирование
Имеется ввиду
дифференцирование функции с предварительным
ее логарифмированием. Такой прием
используется, когда функция не поддается
дифференцированию обычным способом.
Рассмотрим функцию
.
Функция задана в явном виде, но таблицу
производных здесь использовать
невозможно, поскольку функция не является
ни степенной, ни показательной.
Предварительное логарифмирование обеих
частей уравнения с использованием
одного из свойств логарифмов решает
проблему, переводя при этом явную функцию
в неявную.
.
Поскольку заранее известно, что функцией
является
,
дифференцируем обе части полученного
уравнения по
,
.
Есть еще один случай, когда удобно использовать "логарифмическое" дифференцирование. Задана функция
.
Непосредственное дифференцирование этой функции возможно, но приводит к очень громоздким вычислениям. Логарифмируем обе части уравнения, используя при этом одно из свойств логарифмов
,
.
Дифференцируем обе части уравнения по :
,
откуда следует
.
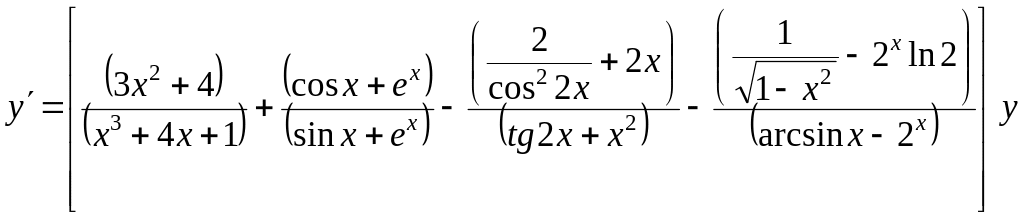Окончательно
.
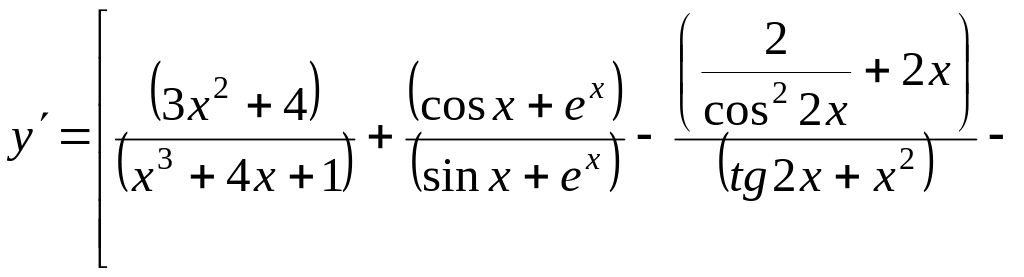
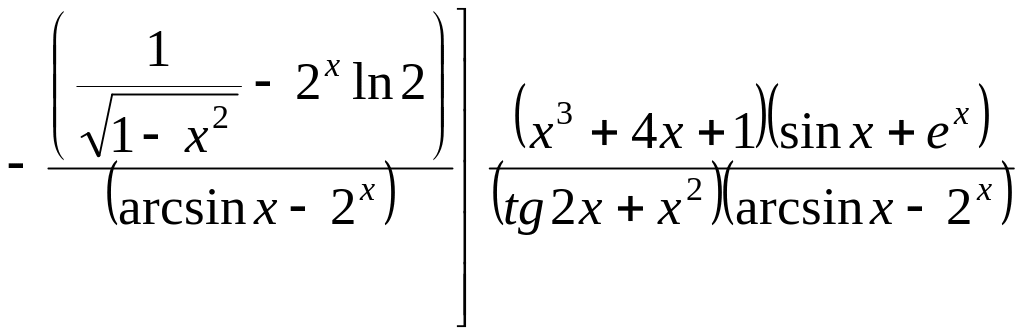Замечание. Возможно логарифмирование по любому основанию, однако, формула производной натурального логарифма проще.
Докажем с помощью
"логарифмического" дифференцирования
не доказанную в общем виде формулу из
таблицы производных. Дано
,
логарифмируем
,
откуда следует
.
Примеры для самостоятельного решения
Вычислить
7.16.
,
7.17.
,
7.18.
,
7.19.
,
7.20.
.