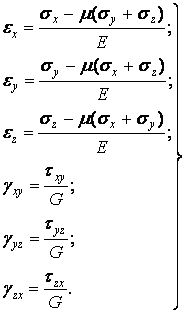8. Що таке лінійна деформація

У пружному тілі під дією прикладених сил відбуваються зміни відстаней між точками або кутів між лінійними елементами, які мають спільну точку. Це явище називається деформацією твердого тіла. В сейсморозвідці пружні хвилі збуджуються вибухами або потужними ударними, або вібродіями на грунт. На значних віддалях від джерела хвиль гірські породи поновлюють свою первісну форму та об’єм миттєво, одразу після припинення дії сил, які викликали деформацію. Такі деформації називають малими. При їх вивченні нехтують другими та вищими степенями зміни віддалей між точками. Часто такі деформації називають лінійними або гуківськими деформаціями.

Деформації розтягу (стиску) – це відносна зміна об’єму тіла без зміни його форми.

(1.1)

де  – лінійна (одноосна) деформація.

Деформація розтягу пропорційна діючому навантаженню :

(1.2)

9. Записати узагальнений закон Гука в деформаціях.

У загальному випадку напруга і деформації описуються тензорами другого рангу в тривимірному просторі (мають по 9 компонент). Зв'язує їх тензор пружних постійних є тензором четвертого рангу і містить 81 коефіцієнт. Внаслідок симетрії тензора , А також тензорів напружень і деформацій, незалежними є тільки 21 постійна. Закон Гука виглядає наступним чином:

де - тензор напружень, - тензор деформацій. Для ізотропного матеріалу тензор містить тільки два незалежних коефіцієнта.

Завдяки симетрії тензорів напруги і деформації, закон Гука може бути представлений в матричної формі.

Або

Узагальнений закон Гука

Щоб встановити залежності між деформаціями й напругами, виділимо з тіла нескінченно малий паралелепіпед (рис.3.1) і розглянемо дію тільки нормальних напруг Різницею напруг на протилежних гранях паралелепіпеду можна зневажити, тому що вона приводить до деформацій більш високого порядку малості.

Визначимо подовження ребра паралельного напрузі При дії цієї напруги відповідно до закону Гука (3.12) відбудеться відносне подовження ребра

Напруга викликає аналогічне подовження в напрямку, перпендикулярному ребру

а в напрямку ребра - укорочення, що згідно (3.13) становить

або, з урахуванням виразу деформації

Аналогічно визначається відносне вкорочення ребра при дії напруги

На підставі принципу незалежності дії сил повне відносне подовження ребра можна визначити як суму подовжень від дії кожної напруги:

або

Аналогічно можна визначити лінійні деформації по напрямках двох інших осей:

Відповідно до закону Гука при зсуві (3.14) зв'язок між кутовими деформаціями і дотичними напруженнями можна представити незалежно для кожної із трьох площин, паралельних координатним площинам:

Таким чином, отримані шість формул, які виражають лінійну залежність між складовими деформації і напруг в ізотропному пружному тілі й називаються узагальненим законом Гука: