2. Бурмистрова е.Б., Лобанов с.Г. Математический анализ и дифференциальны уравнения.-м.-Изд. Центр «Академия», 2010.

3. Понтрягин л.С. Обыкновенные дифференциальные уравнения. - м. :Наука, 1961.

4. Арнольд В.И. Обыкновенные дифференциальные уравнения. Учебное пособие для вузов. -М.: Наука, 1984.

Часть вторая. Разностные (рекуррентные) уравнения.

Глава I. Разностные (рекуррентные) уравнения первого порядка.

Разностное уравнение n-ого порядка в нормальной форме. Определение решения уравнения. Задача Коши. Линейное уравнение первого порядка с переменными коэффициентами. Метод вариации постоянной. Примеры: арифметическая прогрессия, геометрическая прогрессия, рост вклада в банке (простые и сложные проценты).

Литература:

1. Бурмистрова е.Б., Лобанов с.Г. Математический анализ и дифференциальны уравнения.-м.-Изд. Центр «Академия», 2010.

2. Гельфонд В.И. Исчисление конечных разностей.-М.: ГИФМЛ, 1959.

3. Романко В.К. Разностные уравнения.-М.:Лаборатория базовых знаний, 2000.

Глава II. Линейные разностные (рекуррентные) уравнения и системы с постоянными вещественными коэффициентами.

Линейное однородное разностное уравнение n-ого порядка. Линейное пространство его решений. Фундаментальная система решений. Общее решение однородного уравнения. Построение фундаментальной системы решений линейного разностного уравнения с постоянными вещественными коэффициентами. Структура общего решения линейного неоднородного уравнения. Частное решение линейного уравнения с постоянными коэффициентами в случае, когда правая часть - квазимногочлен (резонансный и нерезонансный случаи).

Линейная однородная система разностных уравнений. Линейное пространство её решений. Фундаментальная система решений. Общее решение. Построение фундаментальной системы решений линейной однородной системы разностных уравнений с постоянными вещественными коэффициентами. Структура общего решения неоднородной системы линейных разностных уравнений. Решение систем методом исключения.

Литература:

1. Бурмистрова е.Б., Лобанов с.Г. Математический анализ и дифференциальны уравнения.-м.-Изд. Центр «Академия», 2010.

2. Гельфонд В.И. Исчисление конечных разно стей.-М.: ГИФМЛ, 1959.

3. Романко В.К. Разностные уравнения.-М.:Лаборатория базовых знаний, 2000.

Глава III. Устойчивость положения равновесия разностных уравнений и систем разностных уравнений.

Определение устойчивости решений разностных уравнений и систем. Положение равновесия. Критерий устойчивости решений линейных разностных уравнений и систем с постоянными вещественными коэффициентами. Достаточное условие существования устойчивого положения равновесия нелинейного автономного уравнения первого порядка. Примеры разностных уравнений первого порядка в экономике: паутинообразная модель, динамика дохода в упрощённой модели Кейнса. Примеры разностных уравнений второго порядка в экономике: паутинообразная модель с обучением, модель делового цикла Самуэльсона - Хикса (мультипликатор - акселлератор).

Литература:

1. Бурмистрова Е Б., Лобанов С.Г. Математический анализ и дифференциальны уравнения.-М.-Изд. центр «Академия», 2010.

2. Романко В.К. Разностные уравнения.-М.:Лаборатория базовых знаний, 2000.

3. Chiang Alpha С. Fundamental methods of mathematical economics. Mc.Grow-Hill, 1984.

4. Смирнов А.Д. Лекции по макроэкономическому моделированию . -М.:Изд-во ГУВШЭ, 2000.

Типовые вопросы и задачи для контрольных, зачетной и экзаменационной работ:

1. Решите задачу Коши и укажите промежуток наибольшей длины, на котором решение этой задачи определено.

2. Решите задачу Коши и вычислите для

решения этой задачи значение .

3. Найдите решение уравнения , удовлетворяющее условию . Вычислите для этого решения значение .

4. Вычислите действительную часть числа .

5. Найдите все решения уравнения .

6. Решите задачу Коши и вычислите для решения этой задачи значение .

7. Для последовательности , удовлетворяющей рекуррентному уравнению и условию , вычислите величину .

8. Укажите все возможные значения дроби для всех тех решений рекуррентного уравнения , для которых она определена.

9. Решите систему уравнений

10. Решите неоднородную систему уравнений

и изобразите фазовый портрет однородной системы.

11. Найдите все значения параметра , при которых нулевое решение уравнения асимптотически устойчиво.

12. Укажите все возможные значения дроби для всех тех решений уравнения , для которых она определена.

13. Решите уравнение .

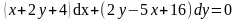14. Решите уравнение .

15. Решите уравнение

16. Решите одну из систем уравнений

или

17. Решите уравнение .

18. Решите уравнение .

19. Решите задачу Коши .

20. Решите задачу Коши .

21. Решите уравнение .

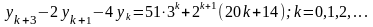22. Решите уравнение .

23. Решите уравнение .

24. Найдите положения равновесия системы уравнений

определите их характер и начертите фазовые траектории соответствующих линеаризованных систем .