Обобщенный метод наименьших квадратов.

При нарушении гомоскедастичности и наличии автокорреляции ошибки следует традиционный МНК заменить обобщенным МНК.

Он применяется к преобразованным данным и позволяет получать оценки, обладающие несмещенностью и имеющие меньше выборочные дисперсии. Используем обобщенный метод наименьших квадратов для корректировки гетероскедастичности.

Предполагаем, что , а дисперсия не остается неизменной для разных значений фактора и пропорциональна величине K_i, т.е.

где - дисперсия ошибки при конкретном i-том значении фактора;

- постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков;

- коэффициент пропорциональности, меняющийся с изменением величины фактора, что и обусловливает неоднородность дисперсии.

Предполагаем, что неизвестна, а по отношении к K выдвигаются определенные гипотезы, характеризующие структуру гетероскедастичности.

В общем виде для уравнения при модель примет вид:

В ней остатки гетероскедастичны. Предполагается отсутствие в них автокорреляции, поделив обе части на (дисперсия остатков будет постоянной, т.е. ), перейдем к временной регрессии на новых переменных с весами

Исходные данные для данного уравнения будут иметь вид:

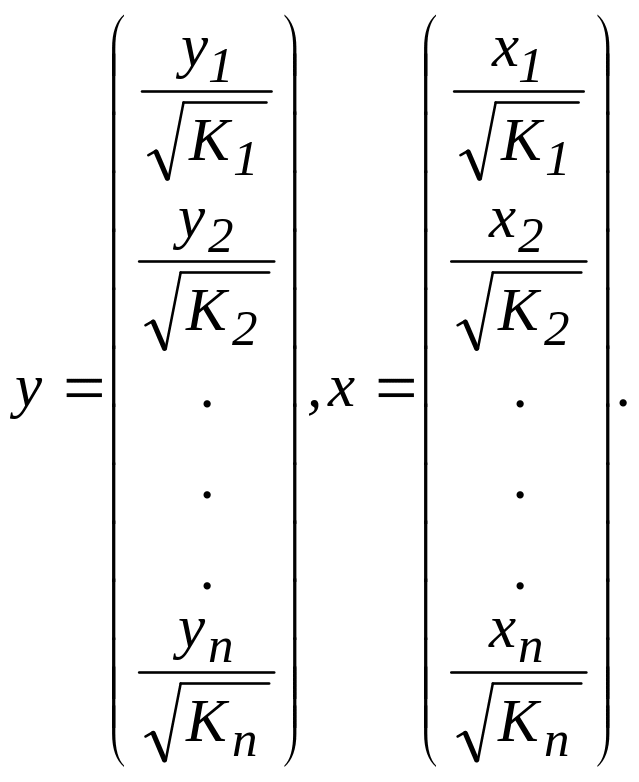
Для оценки параметров такого уравнения приходим к взвешенному МНК, для которого надо минимизировать сумму Ко:

Тогда система нормальных уравнений:

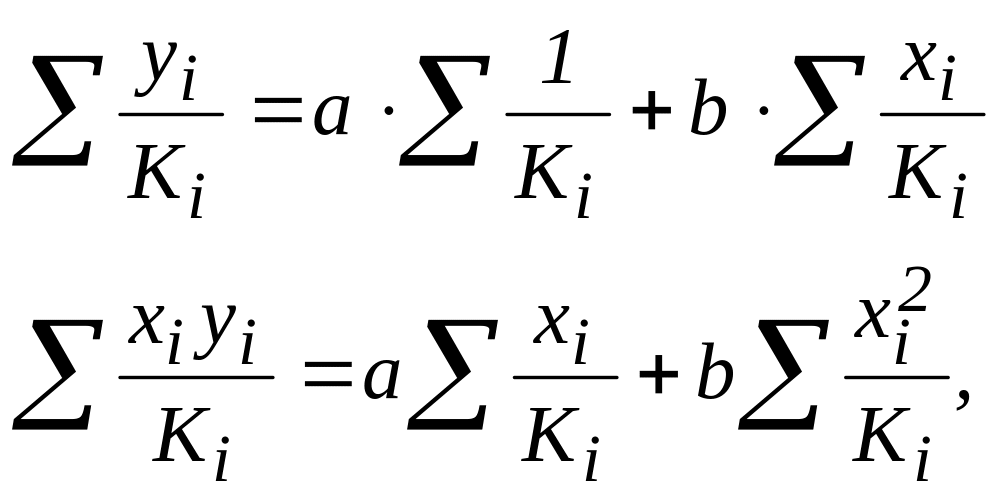
тогда 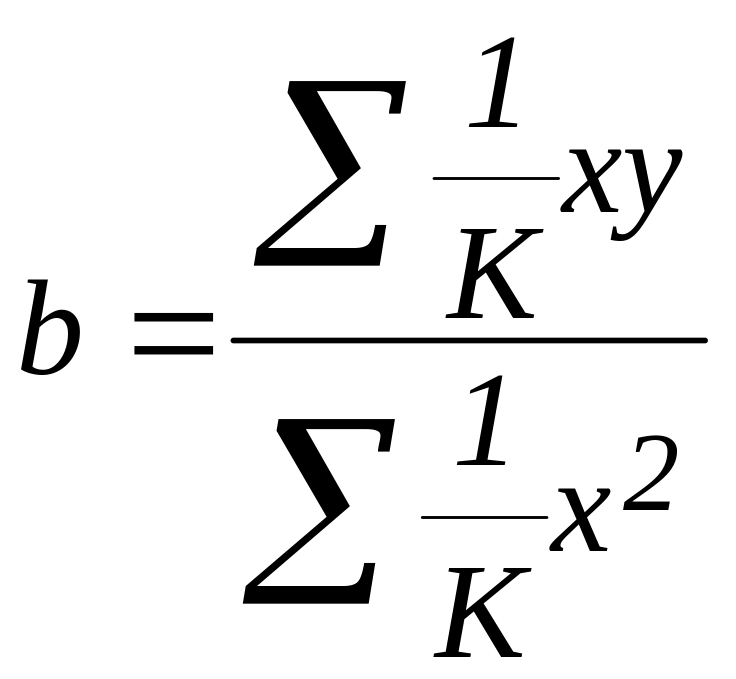(для обыкновенного МНК ).

Для множественной регрессии пусть рассматривается модель вида:

т.к. , то модель примет вид

где ошибки гетероскедастичны.

Для получения уравнения с гомоскедастичными остатками, перейдем к взвешенным переменным:

это уравнение не содержит свободного члена.

Найдя переменные в новом преобразованном виде и применяя обычный МНК к ним, получим новую спецификацию модели:

Параметры такой модели зависят от концепции, принятой для коэффициента K_i. В эконометрических исследованиях часто выдвигается гипотеза о пропорциональности остатков значением фактора. Так, если в уравнении y=a+b₁x₁+b₂x₂+…+b_px_p+E, предположить, что

т.е. K=x₁ и

то обобщенный МНК предполагает оценку параметров следующего трансформированного уравнения:

Применение в этом случае обобщенный метод наименьших квадратов приводит к тому, что наблюдения с меньшими значениями преобразованных переменных имеют при определении параметров регрессии бо́льший вес, чем с первоначальными переменными. Новые преобразованные переменные получают новое экономическое содержание и их регрессия имеет иной смысл, чем регрессия по исходным данным.

73